聚类算法OPTICS的理解及实现
前言
前面给大家介绍到了聚类算法中比较经典的 DBSCAN 算法,对于数据量小而且相对比较密集、密度相似的数据集来说,是比较合适的。那么接下来给大家介绍它的改进版 OPTICS (Ordering points to identify the clustering structure),针对 DBSCAN 在密度差异性较大的数据集中的表现较差的弱点进行优化。
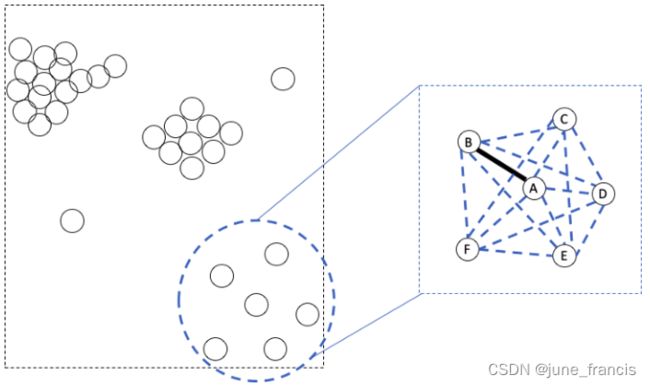
例如下图中所示的数据集中,分别使用上述两种算法进行聚类,可能得到如下结果:
在 DBSCAN 中只会考虑在指定距离参数 eps 范围内的样本点作为当前聚类中心的临近点,很显然这样的处理方式会遗漏掉图中右下角的类簇,不会将它们标记为一个类簇。如果我们将 eps 参数的值设置的更大一点,那么这个类簇会被识别出来,但是,这可能会导致这个类簇左上角的两个类簇被合并到当前类簇中,即图中三个明显的类簇会被识别成一个大的类簇,很明显这样的聚类结果也并不合适。因此,在使用 DBSCAN 进行聚类时我们很难去找到一个合适的 eps 参数来完成最佳的聚类。然而,如果你使用 OPTICS 来完成聚类则完全不用担心发生此类情况。
理解OPTICS的运作机制
在这里假设你已经对 DBSCAN 的运作机制已经比较熟悉了(不熟悉的可以点击上面的超链接快速回顾一下),它仅仅是用一个单一的截断距离来决定两个样本点之间是否是处于各自的邻域之中,但是从上图的案例我们可以看出来这并不是一个理想的解决方案,因为一个较大的截断距离对于数据集中的某一个类簇来说可能是比较合适的,但是对于其它的类簇来说可能就比较小了。就像咱们国家的房价一样,在你的十八线城市的老家一个100万的房子可能就比较贵了,但是这个价格放到超一线城市比如说北京就相当便宜了。这就是为什么我们在看不同组地区(类簇)的房子(样本点)时需要不同的价格标准(聚类标准)是如此的重要。
因此,我们如何能够在 OPTICS 中针对不同的类簇应用不同的距离标准呢?最直接的一种方法就是将样本点与本地环境也就是上下文(local environment Or the context)进行逐一比较。特别地,如果我们想要知道从 A 样本点到 B 样本点之间的距离是大了还是小了,可以和上下文中的所有距离对(邻域中的所有样本点两两之间的距离)进行比较即可。
如上图所示,从样本点A到样本点B之间的距离在所有邻域内两两样本点之间的距离中并不算最大的,那么我们可以认为样本点A与样本点B是互为邻域(A和B互为近邻)。
在这里你可能注意到了几个问题:
- 如何在上面案例中提到的没有明显的样本间隔的情况下去严格定义一个“本地环境(区域)”?
- 如何判断一个本地环境是否值得去进行聚类考察?如果在当前环境中没有充足的距离对来进行比对应该怎么办?
- 真的有必要去比对本地环境中的所有距离对吗?例如,在上图中有必要去比对
A到B之间的距离与B到D之间的距离的大小吗(特别是当我们已经明确的知道B和D就是本地环境中边界上的互为对角位置)?
如果你有上面类似的疑问,那么恭喜你,你正在沿着正确的方向探索 OPTICS 的奥秘。
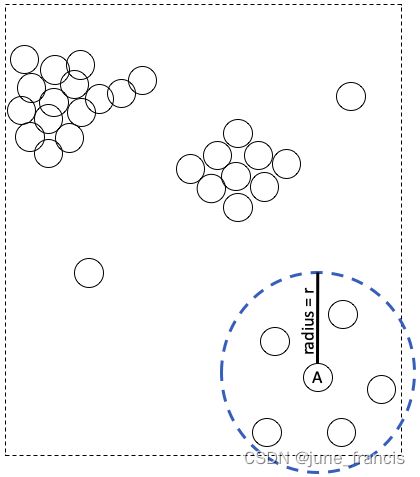
首先,去定义一个“本地环境”,我们需要一个中心点和一个半径(与 DBSCAN 相同)。例如,样本点A是我们要访问的第一个点,这时我们需要去 A 的本地环境周围去进行考察。此时设A为中心点,预定义 r r r 为半径,A的本地环境则表示为如下图所示的圆:
很显然,图中 r r r 的大小此时是最佳选择,因为它完美的覆盖了当前“本地类簇”中的所有样本点。然而,真实场景下我们并不能看到所有数据点的分布情况图或者并不清楚 r r r 取多大对于“本地类簇”来说是最佳的截断距离。因此,我们通常将 r r r 先设为一个相对较大的值,这样做是为了避免当你以样本点A为中心进行聚类时过度关注一个非常小的区域。
其次,一个区域到底的值不值得去进行聚类探索,可以设置一个参数标准来表示形成一个类簇的最小样本数量。例如,在先前一步定义的“本地环境”只有在它至少包含有 N N N 个样本点时(包含中心点)才值得我们去进一步探索。
上图中,我们指定 N = 3 N=3 N=3 ,这意味着一个区域需要至少包含3个样本点才会值得被探索。因此,样本点 P 周围的区域不会被当做“本地环境”进行探索因为在当前半径 r r r 和 N N N 的条件下它没有近邻样本点供它去计算距离和比对。
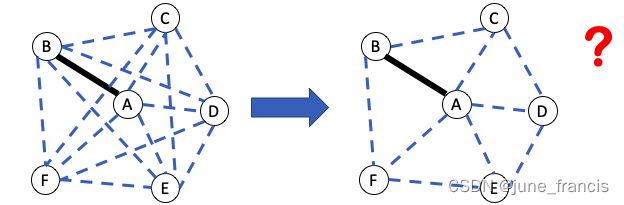
再次,你也可能注意到了,要判断从样本点A到样本点B的距离是否过大,我们没有必要计算“本地区域”中所有样本两两之间的距离,看看如下“本地区域”的距离对:
如上图左所示,样本点A 和 样本点B相连,但是样本点B 和样本点D并不相连。很显然 AB 比BD要短,因此我们没有必要去比较 AB 和BD的长短。是否存在一种方法只考虑相邻点之间的距离呢(如上图右所示)?
实际上,上图所示从左到右减少需要比对的距离对的想法是十分理想的,因为在现实场景中我们会遇到较多样本点以及数据维度较复杂的情况,并且我们很难手动地去选择聚类边界并与AB进行比较,这些无疑会增加我们额外的工作量(计算量)。
作为一种选择,我们是否可以使用一种迭代的方法来解决这个问题呢?例如,我们一个一个的访问本地区域中的样本,每次访问我们只需要记录下从当前点到它相邻点的距离,如此遍历完所有本地区域中的样本,所有相邻点的距离就都被我们记录下来了。这样的话,我们就不需要提前知道整个样本点的分布情况或者在计算所有距离对之后手动的去选择合适距离的样本。
这是一个好的思路,这里我们能否进一步降低完成这些比较操作的复杂度呢?
现在我们重新捋一下当前的问题:
我们为了判断样本点A和样本点B是否在本地区域中是否互为邻域,需要比较AB和本地区域中所有相邻点之间的距离大小。
那么换一种说法,即:我们想要判断样本点B是否属于以样本点A为中心的类簇,需要使用距离计算方法计算出当前两个样本点之间的距离,以判断在对于以A为中心的类簇中,B是否是可达的(reachable)。
这里我们是否可以通过赋予每个样本点一个可达分(reachability score)来表征这种可达或者不可达的关系?如果可达分较大那么这个样本对于当前类来说就是不可达的,反之是可达的。
此时我们来总结一下具体的实施步骤:
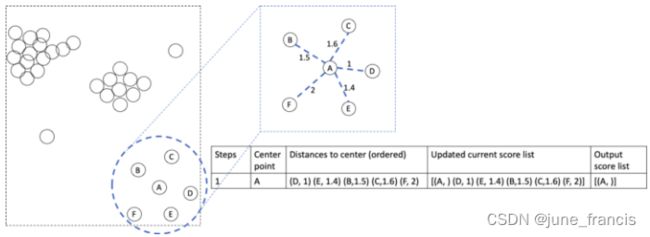
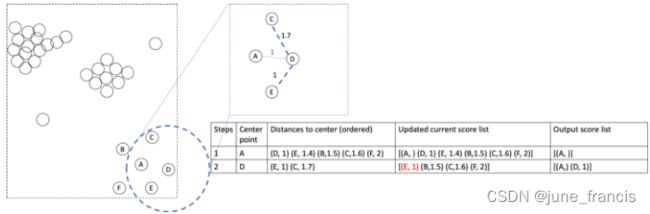
首先,我们要挨个访问本地区域分布在样本点A周围的其它样本点,计算它们与A的距离:AB,AC,AD,AE和AF并记录下来。接下来我们对这些记录下来的距离进行排序并把它们当做当前的可达分。为了避免在下一次迭代中重复到A,AA的可达分也需要进行记录。由于A是起始点所以它没有分数,我们暂时将它用空白表示(或者可以给它赋予一个非常大的值)。
接下来,我们访问当前拥有最小可达分的样本点(样本D),它也是目前离中心点A最近的样本。此时以它为中心点计算邻域中其它的还未被访问到的样本。
如上图所示,我们只需要计算DC和DE即可,因为DA在上一轮的迭代中已经被计算出来了,所以在这里不用再重复计算。接下来我们更新现有的可达分列表,尽可能让它保留最小的分数值。因为E有了新的较小的分数1,比上一步中的1.4要小,所以我们要将E的可达分更新为1.但是C此时的可达分1.7比上一轮1.6要大,这表示在A和D中,C距离A更近,所以我们保留较小值。同理,B和F的可达分在此轮中不会更新并保留上一轮的较小值。
注意我们记录较小可达分的目的是为了声明某个样本点是否属于当前的类簇,因此我们不能去记录较大值。并且,我们不能因为没有使用C的更好的可达分而将它排除在当前类簇之外。
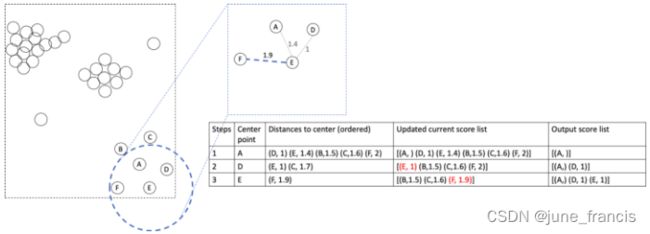
接下来,我们以E为中心点继续计算邻域内未被计算到距离的样本点。
此时我们只需计算出EF即可,值为1.9,根据上述规则,我们更新F的可达分为当前最小的1.9,其它点不更新。
同理,接下来以B为中心进行相应的计算:
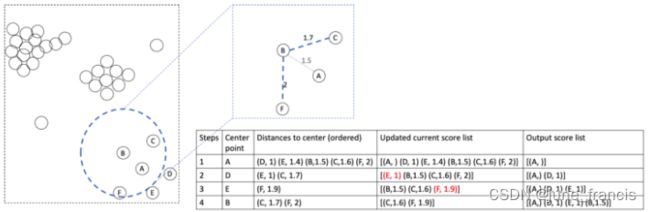
此时只需计算BC和BF即可。
接下来以C为中心点进行相应的计算:
最后以F为中心点进行相应的计算:
到目前为止,我们计算出了当前本地区域(以A为中心点)中所有6个样本点的可达分,在另外一种意义上,我们没有漏掉任何一种邻域内的距离对。相反我们还额外的得到了一个有序的分数列表用来表征某个样本点距离当前考察的类簇的可达性。
好了,到此大家应该能感受到上述的计算方法相比于计算出所有本地区域内的距离对要更加的简单。
实际上,我们可以将上述迭代过程应用到整个数据集。例如,在访问完以F为中心点的类簇后,以A为中心点的本地区域中的所有样本点已经全被我们访问完毕,接下来需要访问的样本就是在数据集中的其它样本点。
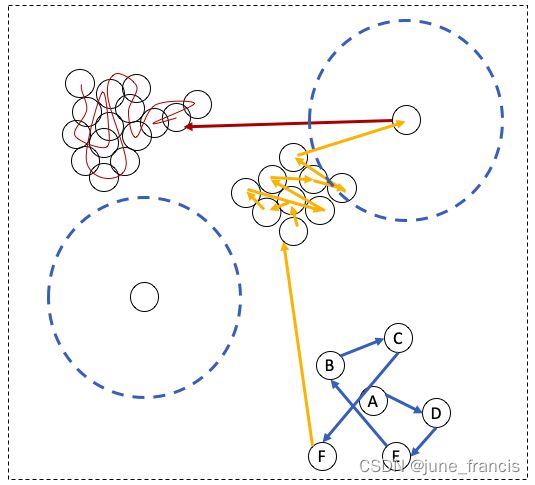
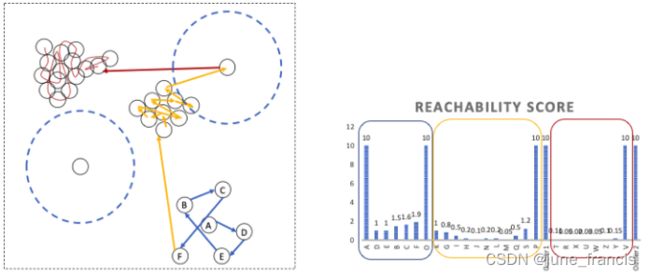
如果我们将所有可能被访问到的中心点的访问路径按照访问的先后顺序画出来,可能是如下图所示:
这条路径你可以想象成一条贪吃蛇想要通过吃掉下一个临近的球(在可达分列表中的)来吃掉图中所有的球(数据点)。
图中右上角看起来孤立的样本点实际上按照我们之前定义的标准(给定的半径 r r r )是有一个符合要求的相邻样本点的,所以,它的访问顺序是橘色区域的最后一个。然而,左下角看起来孤立的样本点按照我们之前定义的标准确实是不存在任何“邻居”,因此这个样本点永远也不会进入到我们的考察范围(因为算上它本身整个类簇只有一个样本点,不符合我们之前设定的类簇必须至少要包含3个样本点的标准)。
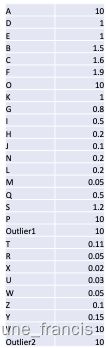
做完这些之后,我们最终得到了一个可达分列表,我们能用它做什么呢?别忘了我们的目的是判断一个样本是否属于当前类簇。例如,下面是我们得到的可达分列表:
我们可以把上述数据使用柱状图进行可视化:
上图右中的柱状图中你会发现三个“峰谷”,他们实际上分别对应图左中的三个类簇。因此,我们可以利用上面得到的可达分列表去检测出不同的类簇而不管它们是否有不同的密度。
同样的,你能发现这三个类簇中左上角那个棕色的类簇的密度相对较大,对应右图中有更深“峰谷”的可达分柱状图,更浅“峰谷”的柱状图数据则对应右下角蓝色的更加稀疏的类簇。
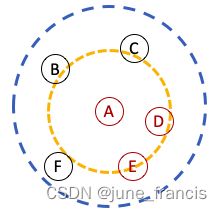
现在因为我们之前规定一个邻域内必须包含至少3个样本点我们才能继续下一步的探索,换言之我们可以把这三个互为邻域的样本点作为当前类簇的核心区域。实际上在这里我们并不关心其它点是否落在核心区域内,为了进一步简化簇内的距离计算,处在核心区域内的样本点,我们可以把它们的可达分设为核心区域的半径。
例如,在下图中,以A为中心以 r r r 为半径的区域包含6个样本点,它的核心区域是由A,D和E组成的(因为在满足N=3的前提条件下D和E是最靠近A的样本点)。很明显D在核心区域,那么我们不用去详细计算AD的实际距离是多少了(是一个较小的值),我们可以简单的将核心区域的半径赋值为D的可达分。
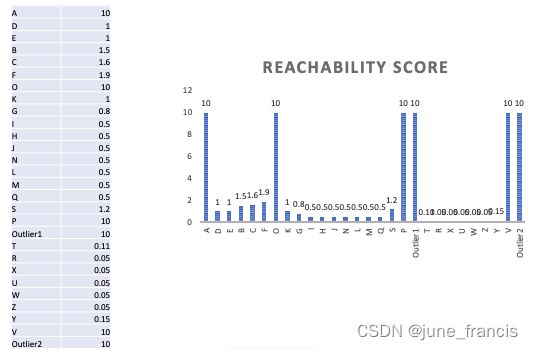
在按照上述的核心区域简化过程将可达分进行简化后,最终我们在可达分列表中得到的最小值就是那些核心区域的大小。有些同学可能会问我们为什么要这样做,首先,这是为了避免在可达分列表中记录太多无用的较小的值;其次,为了能在柱状图中可视化时让“峰谷”更加的平滑(如下图所示)。
好了,如果你能坚持看到这里,那么对于 OPTICS 的运作机制就完全能理解了。接下来我们按照官方的描述再对这一过程进行归纳:
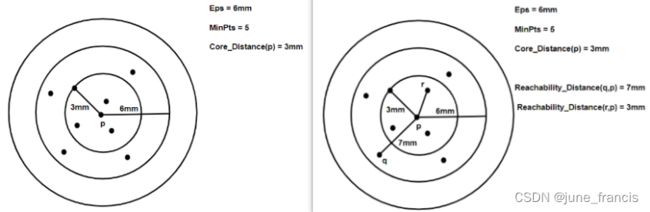
OPTICS的基本思想实际上和DBSCAN的十分相似,但是它比DBSCAN多两个概念;- 在
OPTICS中每个样本点被赋予了一个叫做核心距离(core distance)的概念,它被用于描述此样本点与形成聚类需要的最少的最邻近的 M i n P t s t h MinPtsth MinPtsth 个样本点之间的距离,还有一个叫做可达距离(reachability distance)的概念,它被用于描述一个样本点p到另一个样本点o之间的距离,或者p的核心距离(肯定比可达距离要大)。
上述官方描述中的两个概念 core distance 和 reachability distance 实际上就是上面案例中我们描述的核心距离和可达分列表中记录的可达分,核心距离在这里作为一个阈值用来近似核心区域样本点之间的可达距离。
那么有的同学这里会有疑问了,上面案例里我们可以将排序后的可达分列表进行可视化,但是在实际实现的时候不可能通过我们的肉眼去观察得到对应的可能聚类点,我们还需要通过一种计算方式来快速计算并得到形成可能类簇的样本点集合。
在scikit-learn中实现的OPTICS算法中,实际上是实现了论文: [Ankerst, Mihael, Markus M. Breunig, Hans-Peter Kriegel, and Jörg Sander. “OPTICS: ordering points to identify the clustering structure.” ACM SIGMOD Record 28, no. 2 (1999): 49-60.](Ankerst, Mihael, Markus M. Breunig, Hans-Peter Kriegel, and Jörg Sander. “OPTICS: ordering points to identify the clustering structure.” ACM SIGMOD Record 28, no. 2 (1999): 49-60.)中包含的思想,通过引入坡度(degree of steep),来表征可达分列表中相邻点之间可达分的差距的大小,来完成快速获取聚类集合的目的,那么下面我们简单的过一下论文中设计的重要思想,感兴趣的同学可以去仔细研究一下原论文:
目标:首先识别出潜在的类簇起始点和类簇终止点(根据上面的案例我们知道可达分柱状图中明显的“峰谷”所包含的样本点极有可能会形成一个类簇,那么这个“峰谷”的起点和终止点正好符合这里的要求),那么有了这些起始点和终止点之后,我们只需要成对匹配它们即可得到不同的可能的类簇。
以上图为例,在真实场景中类簇的起始位置和终止位置并不都是非常陡峭的(steep points),上图第一个类簇中包含了坡度非常高的点A和点B,但是第二个类簇到终止点D之前包含了一些并不是非常陡峭的点,为了捕获或者自定义这样包含不同梯度的场景,引入了参数 ξ \xi ξ ,有如下关于 ξ 梯 度 点 \xi 梯度点 ξ梯度点 的相关概念:
ξ 梯 度 向 上 点 : U p P o i n t ξ ( p ) ⟺ r ( p ) ≤ r ( p + 1 ) × ( 1 − ξ ) \xi 梯度向上点:UpPoint_{\xi} (p) \iff r(p) \leq r(p+1) \times (1-\xi) ξ梯度向上点:UpPointξ(p)⟺r(p)≤r(p+1)×(1−ξ)
其中: p ∈ { 1 , 2 , . . . , n − 1 } p \in \{1, 2, ..., n-1\} p∈{1,2,...,n−1} , p p p 是可达分列表中的样本点, r ( p ) r(p) r(p) 是这个样本点的可达分(reachability score)。
同理:
ξ 梯 度 向 下 点 : D o w n P o i n t ξ ( p ) ⟺ r ( p ) × ( 1 − ξ ) ≤ r ( p + 1 ) \xi 梯度向下点:DownPoint_{\xi} (p) \iff r(p) \times (1-\xi) \leq r(p+1) ξ梯度向下点:DownPointξ(p)⟺r(p)×(1−ξ)≤r(p+1)
上图中大部分类簇的起始和结束位置都是由一些 ξ 梯 度 向 上 点 \xi 梯度向上点 ξ梯度向上点 组成的,这些点后面还包含一部分平滑的区域,我们一起叫做坡度区域(steep area),当然,坡度区域后面包含的平滑区域中,所包含的点不能超过指定阈值,这里的指定阈值指的是 M i n P t s MinPts MinPts ,因为 M i n P t s MinPts MinPts 个连续的非坡度点可被认为是另外一个单独的类簇,这些点不能是坡度区域的一部分。那么我们希望的是坡度区域的范围足够大,关于坡度区域( ξ − s t e e p a r e a \xi -steep \; area ξ−steeparea)的条件限制有如下这些:
在可达分列表样本组成的连续区间 I = [ s , e ] I = [s, e] I=[s,e],如果满足如下条件,则它被称为 ξ − 坡 度 向 上 区 间 ( ξ − s t e e p u p w a r d a r e a ) \xi-坡度向上区间(\xi-steep \; upward \; area) ξ−坡度向上区间(ξ−steepupwardarea):
-
s s s 是一个 ξ − 坡 度 向 上 的 点 \xi - 坡度向上的点 ξ−坡度向上的点 : U p P o i n t ξ ( s ) UpPoint_{\xi}(s) UpPointξ(s) ;
-
e e e 是一个 ξ − 坡 度 向 上 的 点 \xi - 坡度向上的点 ξ−坡度向上的点 : U p P o i n t ξ ( s ) UpPoint_{\xi}(s) UpPointξ(s) ;
-
在区间 s s s 和 e e e 之间的任意一点不能小于它的前一个点:
∀ x , s < x ≤ e : r ( x ) ≥ r ( x − 1 ) \forall x,\; s \lt x \le e \; : \; r(x) \ge r(x-1) ∀x,s<x≤e:r(x)≥r(x−1)
-
I I I 不能包含超过 M i n P t s MinPts MinPts 个连续的 非 ξ − 坡 度 上 升 非\xi-坡度上升 非ξ−坡度上升 的点:
∀ [ s ‾ , e ‾ ] ⊆ [ s , e ] : ( ( ∀ x ∈ [ s ‾ , e ‾ ] : ¬ U p P o i n t ξ ( x ) ) ⇒ e ‾ − s ‾ < M i n P t s ) \forall [\overline{s},\overline{e}] \; \subseteq \; [s, e] : ((\forall x \in [\overline{s},\overline{e}] : \lnot UpPoint_{\xi}(x)) \Rightarrow \overline{e} - \overline{s} \lt MinPts) ∀[s,e]⊆[s,e]:((∀x∈[s,e]:¬UpPointξ(x))⇒e−s<MinPts)
-
I I I 是极大值: ∀ J : ( I ⊆ J , U p A r e a ξ ( J ) ⇒ I = J ) \forall J : (I \subseteq J, \; UpArea_{\xi}(J) \Rightarrow I=J) ∀J:(I⊆J,UpAreaξ(J)⇒I=J) ;
一个 ξ − 坡 度 向 下 区 间 \xi-坡度向下区间 ξ−坡度向下区间 可被同样定义为 ( D o w n A r e a ξ ( I ) DownArea_{\xi}(I) DownAreaξ(I))。
还是以上图为例,第一个和第二个类簇都起始于坡度区域的起始边界点(点 A A A 和 C C C),并且结束于另外的坡度区域终止边界点(点 B B B 和 D D D),而第三个类簇则结束于点 F F F (它处于一直延伸到点 G G G 的坡度区域的中部位置)。有了上述这些定义,我们就能够去定义一个类簇了。
下面给出的关于 ξ − 类 簇 \xi-类簇 ξ−类簇 的定义一共包含了 4 个条件,要记住一个类簇的第一个点(起始点)是坡度区域中最后一个有最大可达分值的点,同理类簇的最后一个点(终点)是坡度区域中有较小可达分值的点。
如果一个区间点 C = [ s , e ] ⊆ [ 1 , n ] C = [s, e] \subseteq [1, n] C=[s,e]⊆[1,n] 满足如下 4 个条件,那么我们则把它叫做 ξ — 类 簇 \xi—类簇 ξ—类簇 :
c l u s t e r ξ ( C ) ⟺ ∃ D = [ s D , e D ] , U = [ s U , e U ] w i t h cluster_{\xi}(C) \iff \exist D = [s_D, \; e_D], \; U = [s_U, \; e_U] \; with clusterξ(C)⟺∃D=[sD,eD],U=[sU,eU]with
-
D o w n A r e a ξ ( D ) ∧ s ∈ D DownArea_{\xi}(D) \land s \in D DownAreaξ(D)∧s∈D ;
-
U p A r e a ξ ( U ) ∧ e ∈ U UpArea_{\xi}(U) \land e \in U UpAreaξ(U)∧e∈U ;
-
a) e − s ≥ M i n P t s e-s \ge MinPts e−s≥MinPts
b) ∀ x , s D < x < e U : ( r ( x ) ≤ m i n ( r ( s D ) , r ( e U ) ) × ( 1 − ξ ) ) \forall x, s_D \lt x \lt e_U : (r(x) \le min(r(s_D),r(e_U)) \times (1-\xi)) ∀x,sD<x<eU:(r(x)≤min(r(sD),r(eU))×(1−ξ)) ;
-
( s , e ) = (s,e) = (s,e)=
{ ( m a x { x ∈ D ∣ r ( x ) > r ( e U + 1 ) } , e U ) i f r ( s D ) × ( 1 − ξ ) ≥ r ( e U + 1 ) ( b ) ( s D , m i n { x ∈ U ∣ r ( x ) < r ( s D ) } ) i f r ( e U + 1 ) × ( 1 − ξ ) ≥ r ( s D ) ( c ) ( s D , e U ) o t h e r w i s e ( a ) \begin{cases} (max\{x \in D \; | \; r(x) \gt r(e_U+1)\}, \; e_U) \quad if \; r(s_D) \times (1-\xi) \ge r(e_U+1) \quad (b) \\ (s_D, \; min\{x \in U \; | \; r(x) \lt r(s_D)\}) \quad if \; r(e_U+1) \times (1-\xi) \ge r(s_D) \quad (c) \\ (s_D, \; e_U) \quad otherwise \quad (a) \end{cases} ⎩⎪⎨⎪⎧(max{x∈D∣r(x)>r(eU+1)},eU)ifr(sD)×(1−ξ)≥r(eU+1)(b)(sD,min{x∈U∣r(x)<r(sD)})ifr(eU+1)×(1−ξ)≥r(sD)(c)(sD,eU)otherwise(a)
这里给出上述几个条件的解释:
-
条件
1和条件2简单的阐明了类簇的起始点被包含在一个 ξ − 坡 度 向 下 区 域 D \xi-坡度向下区域D ξ−坡度向下区域D 中,而它的终止点则被包含在一个 ξ − 坡 度 向 上 区 域 U \xi-坡度向上区域U ξ−坡度向上区域U 中; -
条件
3a表明了在 O P T I C S OPTICS OPTICS 中使用到的核心条件:一个类簇必须包含至少 M i n P t s MinPts MinPts 个点; -
条件
3b则表明了类簇中的所有点的可达分必须要比 D 区 域 D区域 D区域 中第一个点和 U 区 域 U区域 U区域 后的第一个点的可达分低至少 ξ % \xi\% ξ% ; -
条件
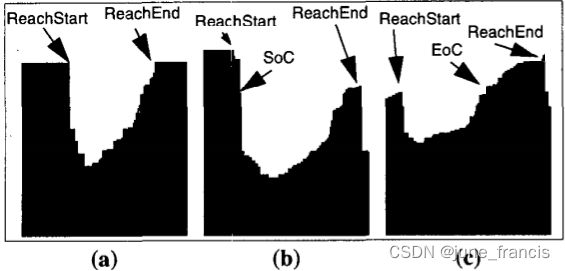
4决定了类簇的起始和终止点。接下来我们依据 D 区 域 D区域 D区域 第一个点(可被叫做 R e a c h S t a r t ReachStart ReachStart)和 U 区 域 U区域 U区域 后的第一个点(可被叫做 R e a c h E n d ReachEnd ReachEnd)的可达分,区分如下图所示的3种情况:-
第一种情况是,如果这两个点的可达分值最多相差 ξ % \xi \% ξ% ,那么这个类簇的起始点是 D 区 域 D区域 D区域 的起点,终点是 U 区 域 U区域 U区域 的最后一个点(如图中
a所示); -
第二种情况是,如果 R e a c h S t a r t ReachStart ReachStart 比 R e a c h E n d ReachEnd ReachEnd 要高至少 ξ % \xi \% ξ% ,那么这个类簇的终点是 U 区 域 U区域 U区域 的最后一个点,但是起始点是 D 区 域 D区域 D区域 中与 R e a c h E n d ReachEnd ReachEnd 可达分值最相近的那个点(如图
b所示起始点是 S o C SoC SoC); -
否则(例如,如果 R e a c h E n d ReachEnd ReachEnd 要比 R e a c h S t a r t ReachStart ReachStart 高至少 ξ % \xi \% ξ% ),那么这个类簇的起点是 D 区 域 D区域 D区域 中的第一个点,终点是 U 区 域 U区域 U区域 中可达分值与 R e a c h S t a r t ReachStart ReachStart 最相近的那个点(如图中
c所示终点是 E o C EoC EoC)。
-
好了,到这里比较重要的一些概念和参数基本上就介绍完毕了,论文中还对寻找最优类簇做了理论优化,这里不再赘述,感兴趣的小伙伴可以去看一看研究研究。
案例及实现
接下来我们使用sklearn中的API来实际演示一下 OPTICS 的聚类过程:
class sklearn.cluster.OPTICS(***, min_samples=5, max_eps=inf, metric=‘minkowski’, p=2, metric_params=None, cluster_method=‘xi’, eps=None, xi=0.05, predecessor_correction=True, min_cluster_size=None, algorithm=‘auto’, leaf_size=30, memory=None, n_jobs=None)
重要参数:
min_samples:一个点被当做核心点时邻域中存在的最少样本点数量,当然,向上坡度区域和向下坡度区域不能有超过 m i n _ s a m p l e s min\_samples min_samples 个连续的非坡度点。这里可以将 m i n _ s a m p l e s min\_samples min_samples 看做是上述流程中的 M i n P t s MinPts MinPts 。一般是0和1之间的小数或者大于1的整数,默认值为5。max_eps:判断一个点是否在另一个点邻域内的最大距离,值越小,最终计算得到目标类簇的时间越短。默认值是np.inf,表示无穷大,意味着它会计算当前所有大小尺寸的类簇。metrics:衡量样本之间距离的方法,默认为minkowski,也可指定为scipy.spatial.distance中的任意一种距离衡量方法。p:当距离衡量方法为minkowski时的参数,1为曼哈顿距离,2为欧氏距离,其它任意值则为闵可夫斯基距离。cluster_method:依据可达分及其排序情况提取类簇的方法。可选值为xi、dbscan。eps:判断一个点是否在另一个点邻域内的最大距离,默认和参数max_eps值一样。只有当参数cluster_method为dbscan时才会使用此参数。xi:此参数决定了在可达分图里构成类簇边界的最小坡度。例如,在可达分图中如果一个点的可达分值最大为它下一个点可达分值的 1 − x i 1-xi 1−xi 倍,那么这个点就是一个向上坡度点,反之则不是。只有当参数cluster_method为xi时才会使用此参数。其值一般介于0到1之间,默认值为 0.05。min_cluster_size:在组成的 OPTICS类簇中包含的最少样本点数。值为介于0到1之间的小数或者大于1的整数,默认值为 None,此时使用的值与参数min_samples一样,只有当参数cluster_method为xi时才能使用此参数。algorithm:搜索近邻点的方法,可选值有auto、ball_tree、kd_tree、brute,默认为auto,即会根据当前的数据自动选择最合适的方法。leaf_size:当参数algorithm指定为BallTree或者KDTree时,用于限制叶子节点包含的样本点数量。这个参数能够影响搜索空间树的构建和查询效率,同样会影响存储这个空间树内存的大小。
接下来我们以官方给的一个案例简单的做一个聚类:
# Authors: Shane Grigsby 得到如下结果图:
这里先是构造了几个类簇样本,这些类簇拥有不同的密度和离散度。
使用 xi 聚类检测方法的OPTICS 可以自动帮助我们在得到的有序样本可达分数据上进行聚类,这里我们还使用了指定可达分阈值进行DBSCAN聚类,可以看到不同的OPTICS的 xi 聚类方法可以通过选择使用合适的可达分阈值的DBSCAN聚类方法进行复现。
参考文献
- https://www.geeksforgeeks.org/ml-optics-clustering-explanation/
- https://towardsdatascience.com/understanding-optics-and-implementation-with-python-143572abdfb6
- https://scikit-learn.org/stable/modules/generated/sklearn.cluster.OPTICS.html
- https://scikit-learn.org/stable/modules/generated/sklearn.cluster.cluster_optics_dbscan.html
- https://scikit-learn.org/stable/auto_examples/cluster/plot_optics.html#sphx-glr-auto-examples-cluster-plot-optics-py
- https://en.wikipedia.org/wiki/OPTICS_algorithm
- https://dl.acm.org/doi/pdf/10.1145/304181.304187