机器学习笔记(十一)聚类算法OPTICS原理和实践
OPTICS聚类算法是基于密度的聚类算法,全称是Ordering points to identify the clustering structure。提到基于密度的聚类算法,应该很快会想到前面介绍的DBSCAN聚类算法,事实上,OPTICS也是为了优化DBSCAN而出现的。
一、原理
在DBSCAN算法中,有两个比较重要的参数:邻域半径eps和核心对象的最小邻域样本数min_samples,选择不同的参数会导致最终聚类的结果千差万别,而在高维数据中,两个参数的联合调参也不是一件容易的事。OPTICS算法的提出就是为了帮助DBSCAN算法选择合适的参数,降低输入参数的敏感度。实际上,OPTICS并不显式的生成数据聚类结果,只是对数据集中的对象进行排序,得到一个有序的对象列表,通过该有序列表,可以得到一个决策图,通过决策图可以选择不同的eps参数进行DBSCAN聚类。在继续阅读下面的内容之前,需要先了解DBSCAN的相关内容,因为本文的部分概念来自于DBSCAN。
在DBSCAN的基础上,OPTICS定义了两个新的距离概念:
(1)核心距离
对于一个给定的核心对象X,使得X成为核心对象的最小邻域距离 r 就是X的核心距离。这句话乍一看有点绕,其实仔细读两遍就明白了,假如在DBSCAN中我们定义 eps = 1.2 和 min_samples=5,X在eps = 1.2的邻域内有8个样本点,则X是核心对象,但是我们发现距离X最近的第5个点和X的距离是0.8,那么核心对象 X 的核心距离就是 0.8,显然每个核心对象的核心距离并不都是相同的。参考图1,注意在计算 min_samples 的时候,一般也包括样本点自身,所以只需在P点eps邻域内找到7个点,那么P点就是核心点。
(2)可达距离
如果X是核心对象,则对象 Y 到对象 X 的可达距离就是Y到X的欧氏距离和X的核心距离的最大值,如果X不是核心对象,则Y和X之间的可达距离就没有意义(不存在可达距离),显然,数据集中有多少核心对象,那么 Y 就有多少个可达距离。在下文介绍 API 的时候,我们会介绍在OPTICS中,一般默认设置 eps 为无穷大,即只要数据集的样本数不少于 min_samples,那么任意一个样本点都是核心对象,即都有核心距离,且任意两个对象之间都存在可达距离。
1.1 算法描述
OPTICS的原理并不复杂,只不过大多数介绍资料都喜欢列举一些广义的算法流程或者伪代码,虽然满足算法介绍的严谨性,但是阅读起来不免显得晦涩难懂,没有阅读的欲望。因此,和之前的文章一样,本文也是先介绍OPTICS的标准算法流程,然后再以案例的形式介绍流程的具体执行逻辑,如果算法流程不能一下子理解的话,可以先跳过直接看后面的案例,然后再回来看标准流程。
OPTICS算法流程:
- 已知数据集 D,创建两个队列,有序队列O和结果队列R(有序队列用来存储核心对象及其该核心对象的密度直达对象,并按可达距离升序排列;结果队列用来存储样本点的输出次序。可以把有序队列里面放的理解为待处理的数据,而结果队列里放的是已经处理完的数据)。
- 如果D中所有点都处理完毕或者不存在核心点,则算法结束。否则,选择一个未处理(即不在结果队列R中)且为核心对象的样本点 p,首先将 p 放入结果队列R中,并从D中删除 p。然后找到 D 中 p 的所有密度直达样本点 x,计算 x 到 p 的可达距离,如果 x 不在有序队列 O 中,则将 x 以及可达距离放入 O 中,若 x 在 O 中,则如果 x 新的可达距离更小,则更新 x 的可达距离,最后对 O 中数据按可达距离从小到大重新排序。
- 如果有序队列 O 为空,则回到步骤2,否则取出 O 中第一个样本点 y(即可达距离最小的样本点),放入 R 中,并从 D 和 O 中删除 y。如果 y 不是核心对象,则重复步骤 3(即找 O 中剩余数据可达距离最小的样本点);如果 y 是核心对象,则找到 y 在 D 中的所有密度直达样本点,并计算到 y 的可达距离,然后按照步骤2将所有 y 的密度直达样本点更新到 O 中。
- 重复步骤2、3,直到算法结束。最终可以得到一个有序的输出结果,以及相应的可达距离。
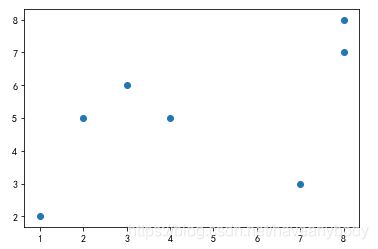
已知样本数据集为:D = {[1, 2], [2, 5], [8, 7], [3, 6], [8, 8], [7, 3], [4,5]},为了更好地标识索引,我们以表格标识数据如下:
| 索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 核心对象 |
| 元素 | (1, 2) | (2, 5) | (8, 7) | (3, 6) | (8, 8) | (7, 3) | (4, 5) | |
| 核心距离 | 3.16 | 1.41 | 1.0 | 1.41 | 1.0 | 3.61 | 1.41 | |
| 第一次可达距离 | inf | 3.16 | 8.60 | 4.47 | 9.21 | 6.08 | 4.24 | 0 |
| 第二次可达距离 | -- | -- | 6.32 | 1.41 | 6.70 | 5.38 | 2.0 | 1 |
| 第三次可达距离 | -- | -- | 5.09 | -- | 5.39 | 5.0 | 1.41 | 3 |
| 第四次可达距离 | -- | -- | 4.47 | -- | 5.0 | 3.61 | -- | 6 |
| 第五次可达距离 | -- | -- | 4.12 | -- | 5.0 (5.10) |
-- | -- | 5 |
| 第六次可达距离 | -- | -- | -- | -- | 1.0 | -- | -- | 2 |
| 输出顺序 | 0 | 1 | 5 | 2 | 6 | 4 | 3 | |
| 可达距离 | inf | 3.16 | 4.12 | 1.41 | 1.0 | 3.61 | 1.41 |
假设eps = inf,min_samples=2,则数据集D在OPTICS算法上的执行步骤如下:
- 计算所有的核心对象和核心距离,因为 eps 为无穷大,则显然每个样本点都是核心对象。因为 min_samples=2,则每个核心对象的核心距离就是离自己最近样本点到自己的距离(样本点自身也是邻域元素之一),具体如上表所示。
- 随机在 D 中选择一个核心对象,假设选择 0 号元素,将 0 号元素放入 R 中,并从 D 中删除。因为 eps = inf,则其他所有样本点都是 0 号元素的密度直达对象,计算其他所有元素到 0 号元素的可达距离(实际就是计算所有元素到 0 号元素的欧氏距离,如表1第一次可达距离),并按可达距离排序,添加到序列 O 中。
- 此时 O 中可达距离最小的元素是 1 号元素,取出 1 号元素放入 R ,并从 D 和 O 中删除,因为 1 号元素是核心对象,找到 1 号元素在 D 中的所有密度直达对象(剩余的所有样本点),并计算可达距离,同时更新 O(如表1第二次可达距离)。
- 此时 O 中可达距离最小的元素是 3 号元素,取出 3 号元素放入 R ,并从 D 和 O 中删除,因为 3 号元素是核心对象,找到 3 号元素在 D 中的所有密度直达对象(剩余的所有样本点),并计算可达距离,同时更新 O(如表1第三次可达距离)。
- 此时 O 中可达距离最小的元素是 6 号元素,取出 6 号元素放入 R ,并从 D 和 O 中删除,因为 6 号元素是核心对象,找到 6 号元素在 D 中的所有密度直达对象(剩余的所有样本点),并计算可达距离,同时更新 O(如表1第四次可达距离)。
- 此时 O 中可达距离最小的元素是 5 号元素,取出 5 号元素放入 R ,并从 D 和 O 中删除,因为 5 号元素是核心对象,找到 5 号元素在 D 中的所有密度直达对象(剩余的所有样本点),并计算可达距离,同时更新 O(如表1第五次可达距离)。注意本次计算的4号元素到5号元素的可达距离是5.10,大于5.0,因此不更新4号元素的可达距离。
- 此时 O 中可达距离最小的元素是 2 号元素,取出 2 号元素放入 R ,并从 D 和 O 中删除,因为 2 号元素是核心对象,找到 2 号元素在 D 中的所有密度直达对象(剩余的所有样本点),并计算可达距离,同时更新 O(如表1第六次可达距离)。
- 此时 O 中可达距离最小的元素是 4 号元素,取出 4 号元素放入 R ,并从 D 和 O 中删除,因为 D 已空,O 也已空,程序结束。根据表1,最终的结果序列 R 的元素索引输出顺序为:0、1、3、6、5、2、4,可达距离如表1最后一行所示。
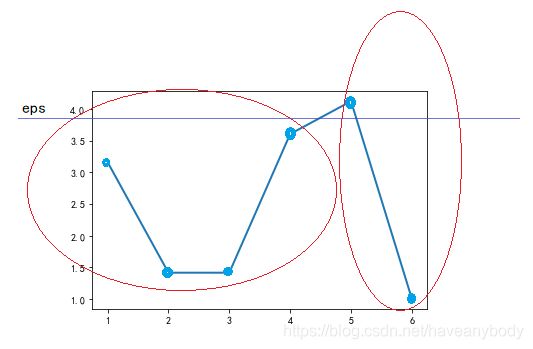
我们按照最终的输出顺序绘制可达距离图(注意,因为第一个元素没有可达距离,或者说可达距离是无穷大,故图中没有标出 0 号元素的可达距离):
可以发现,可达距离呈现两个波谷,也即表现为两个簇,波谷越深,表示簇越紧密,只需要在两个波谷之间取一个合适的 eps 分隔值(图中蓝色的直线,例如两个可达距离的平均值),使用 DBSCAN 算法就会聚类为两个簇。即第一个簇的元素为:0、1、3、6、5;第二个簇的元素为:2、4。下面我们通过sklearn库来验证我们的结果。
二、实践
sklearn库同样为我们封装了 OPTICS 算法的API,供我们直接使用。
2.1 验证
基于1.1的数据集,使用OPTICS验证算法结果如下:
from sklearn.cluster import OPTICS
import numpy as np
X = np.array([[1, 2], [2, 5], [8, 7],[3, 6], [8, 8], [7, 3], [4,5]])
clustering = OPTICS(min_samples=2).fit(X)
print(clustering.core_distances_)
'''
array([3.16227766, 1.41421356, 1. , 1.41421356, 1. ,3.60555128, 1.41421356])
'''
print(clustering.ordering_)
'''
array([0, 1, 3, 6, 5, 2, 4])
'''
print(clustering.reachability_)
'''
array([inf, 3.16227766, 4.12310563, 1.41421356, 1. ,3.60555128, 1.41421356])
'''
print(clustering.labels_)
'''
array([0, 0, 1, 0, 1, 0, 0])
'''根据图3,选择 eps=3.8,使用DBSCAN算法验证如下:
import sklearn
db = sklearn.cluster.DBSCAN(eps=3.8,min_samples=2).fit(X)
db.labels_
## array([0, 0, 1, 0, 1, 0, 0])参考资料
[1] https://blog.csdn.net/PRINCE2327/article/details/110412944