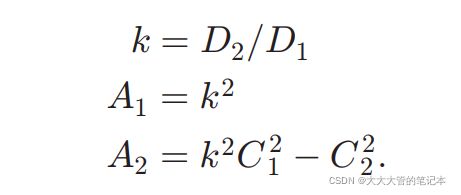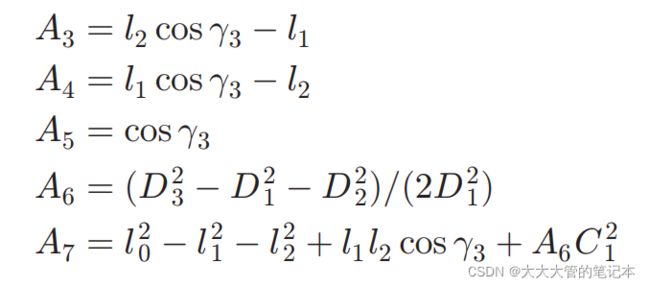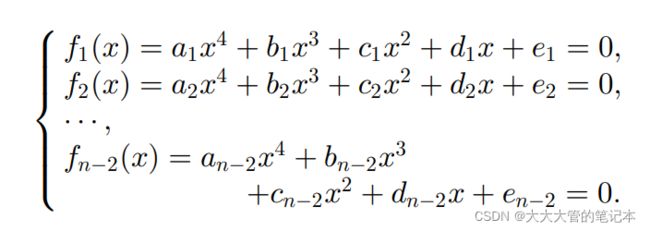RPnP算法原文及代码解析
(有不对的地方希望得到您的指正~~)
RPnP(Robust Perspective-n-Point)是一种快速且具有鲁棒性的PnP求解方法。在2D-3D点较少的情况下,能取得较理想的计算效果。并且其结果远优于EPnP+GN,是目前解决PnP问题的最有效的方法之一。由于RPnP算法是在PST(Perspective Similar Triangle)算法之上,提出来的,故在解析RPnP前,需简单介绍一下PST算法。
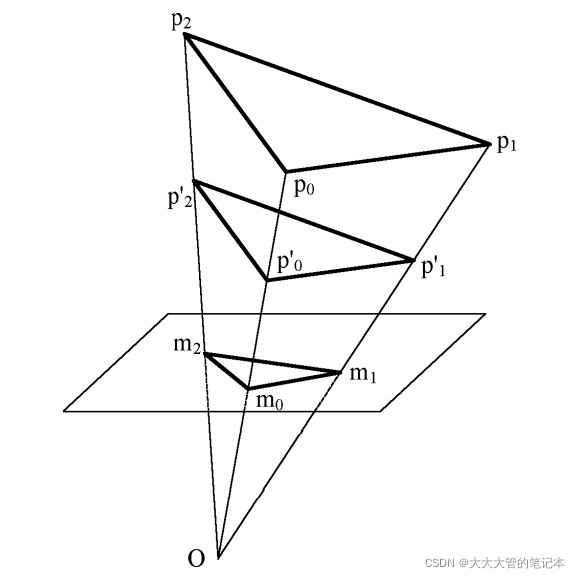
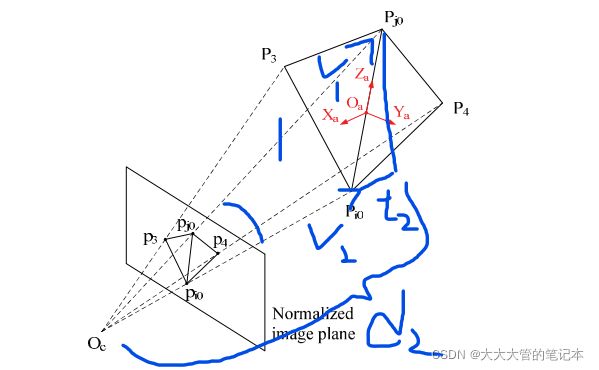
PST算法是为了解决P3P问题,提出的一种透视相似三角形的方法。如上图所示,最上面的三角形为物体坐标系,中间为最上面三角形的相似三角形。
上图为PST的原理图。简单来看,PST算法是通过设一个3D点(l0)到光心(O)的距离已知,通过几何限制条件求出t2与t1的结果,再由3D点中的距离关系,通过比例获得出三角形在空间中的位置(详细过程请看原文)。在PST算法的原文中将各个限制条件,融合在一起,得到了一个4次方程:
其中:
但解的结果最多有4个,故依旧需要第4个点作为限制点,来确定物体坐标系与相机坐标系的转换关系。
RPnP将图像坐标系中距离最远的两个点,看作初始点(文中解释是因为最长边受到噪声的影响最小)。并将3D点中的n个点,看作n-2个三角形(即每个点都与两个初始点形成三角形)。再运用PST算法就可以得到下面的方程组:
F'为一个7阶方程,通过特征值的方式,可以求解出极值点。即求解出当前三角形在空间中的位姿。在原文中将Pi0与Pj0看作Z轴,通过叉乘的方式获得当前三角形在相机坐标系下的物体坐标系(详细过程请看原文)。如下公式所述:
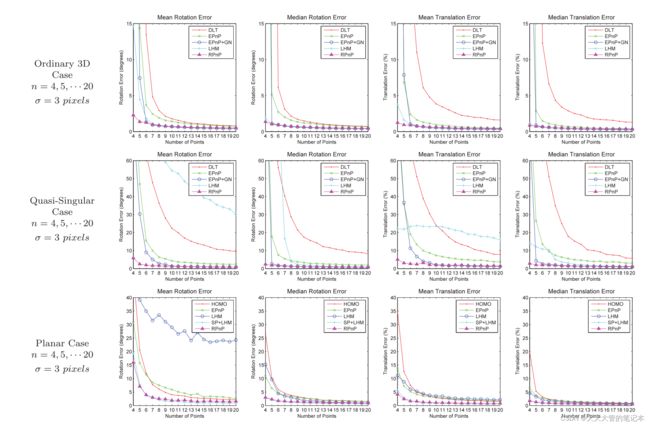
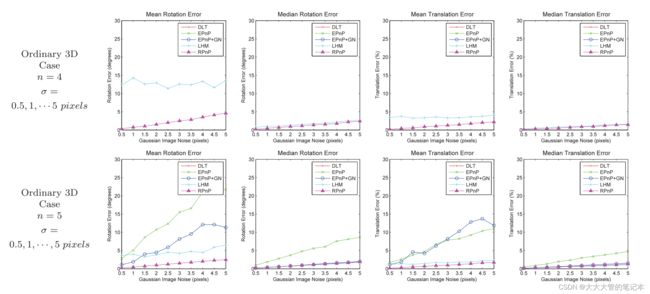
通过上式,使用SVD的方法,可将n-2个三角形的物体坐标系与相机坐标系的转换关系求解出来。计算各个转换关系对应的重投影误差,取最小的重投影误差作为结果。下图为,对比结果。
以下为matlab的RPnP的代码解析(代码与实际中的原文有些小地方不太一样)。
上图为个人对代码中参数的理解
function [R t]= RPnP(XX,xx)
R= []; t= [];
n= length(xx);
XXw= XX; % 原物体坐标系中的点
xxv= [xx; ones(1,n)]; % 图像坐标系中的点
% 归一化
for i=1:n
xxv(:,i)= xxv(:,i)/norm(xxv(:,i));
end
% 选择在图像平面中投影长度最长的边$P_{i1}P_{i2}$。
lmin= inf;
i1= 0; i2= 0;
for i= 1:n-1
for j= i+1:n
l= xxv(1,i)*xxv(1,j)+xxv(2,i)*xxv(2,j)+xxv(3,i)*xxv(3,j);
if l < lmin
i1= i;
i2= j;
lmin= l;
end
end
end
% 计算旋转矩阵 $O_aX_aY_aZ_a$.
% 距离最远的两个点P1,P2(此处为图像坐标系中距离最远的点与对应的物体坐标系中的点)
p1= XX(:,i1);
p2= XX(:,i2);
p0= (p1+p2)/2; % 新物体坐标系原点
x= p2-p0; x= x/norm(x); % 归一化之后的新物体坐标系的x轴单位向量
if abs([0 1 0]*x) < abs([0 0 1]*x)
z= xcross(x,[0; 1; 0]); z= z/norm(z);
y= xcross(z, x); y= y/norm(y); %叉乘后的y轴单位向量
else
y= xcross([0; 0; 1], x); y= y/norm(y);
z= xcross(x,y); z= z/norm(z); %叉乘后的z轴单位向量
end
Ro= [x y z]; % 原物体坐标系到新物体坐标系的旋转矩阵
% 将参考点从原始物体坐标系转换为新的坐标系$O_aX_aY_aZ_a$。(以下为称为物体坐标系)
XX= Ro.'*(XX-repmat(p0,1,n));
% 将n点集划分为(n-2)个3点子集,并建立P3P方程
v1= xxv(:,i1); % 像平面下pi坐标
v2= xxv(:,i2); % 像平面下pj坐标
cg1= v1.'*v2; % pi*pj,即两点夹角余弦值
sg1= sqrt(1-cg1^2); % 两点夹角正弦值
D1= norm(XX(:,i1)-XX(:,i2)); % PiPj的长度
D4= zeros(n-2,5);
if 0 % 确定F',成本函数的偏差。
j = 0;
for i= 1:n
if i == i1 || i == i2
continue;
end
j= j+1;
vi= xxv(:,i);
cg2= v1.'*vi; % Pi坐标和其他点的余弦值
cg3= v2.'*vi; % Pj坐标和其他点的余弦值
sg2= sqrt(1-cg2^2); % Pi坐标和其他点的正弦值
D2= norm(XX(:,i1)-XX(:,i)); %物体坐标系下Pi点与其他点的长度
D3= norm(XX(:,i)-XX(:,i2)); %物体坐标系下Pj点与其他点的长度
% 从每个子集中获得P3P方程的系数。
D4(j,:)= getp3p(cg1,cg2,cg3,sg1,sg2,D1,D2,D3); % (n-2)x5的系数矩阵
end
% 得到七阶多项式,即成本函数的偏差。
D7= zeros(1,8);
for i= 1:n-2
D7= D7+ getpoly7(D4(i,:)); % F(x)*F'(x)的7阶系数矩阵
end
else % =======================================================================
%下面的代码与上面的代码相同(介于“if 0”和“else”之间)
%但是当点数较大时,下面的代码比matlab中的前者效率略高,因为使用了点乘运算。
idx= true(1,n);
idx([i1 i2])= false;
vi= xxv(:,idx);
cg2= vi.'*v1;
cg3= vi.'*v2;
sg2= sqrt(1-cg2.^2);
D2= cg2;
D3= cg2;
didx= find(idx);
for i= 1:n-2
D2(i)= norm(XX(:,i1)-XX(:,didx(i)));
D3(i)= norm(XX(:,didx(i))-XX(:,i2));
end
A1= (D2./D1).^2;
A2= A1*sg1^2-sg2.^2;
A3= cg2.*cg3-cg1;
A4= cg1*cg3-cg2;
A6= (D3.^2-D1^2-D2.^2)./(2*D1^2);
A7= 1-cg1^2-cg2.^2+cg1*cg2.*cg3+A6.*sg1^2;
D4= [A6.^2-A1.*cg3.^2, 2*(A3.*A6-A1.*A4.*cg3),...
A3.^2+2*A6.*A7-A1.*A4.^2-A2.*cg3.^2,...
2*(A3.*A7-A2.*A4.*cg3), A7.^2-A2.*A4.^2];
F7= [4*D4(:,1).^2,...
7*D4(:,2).*D4(:,1),...
6*D4(:,3).*D4(:,1)+3*D4(:,2).^2,...
5*D4(:,4).*D4(:,1)+5*D4(:,3).*D4(:,2),...
4*D4(:,5).*D4(:,1)+4*D4(:,4).*D4(:,2)+2*D4(:,3).^2,...
3*D4(:,5).*D4(:,2)+3*D4(:,4).*D4(:,3),...
2*D4(:,5).*D4(:,3)+D4(:,4).^2,...
D4(:,5).*D4(:,4)];
D7= sum(F7);
end
% 求代价函数的极小值。
t2s= roots(D7);
maxreal= max(abs(real(t2s)));
t2s(abs(imag(t2s))/maxreal > 0.001)= []; % 虚部过大或过小值置空?
t2s= real(t2s);
D6= (7:-1:1).*D7(1:7);
F6= polyval(D6,t2s); % 求解多项式的值?
t2s(F6 <= 0)= [];
if isempty(t2s)
fprintf('no solution!\n');
return
end
% 从每个局部最小值计算相机姿势。
m= length(t2s);
for i= 1:m
t2= t2s(i);
% 计算旋转矩阵
d2= cg1+t2;
x= v2*d2- v1; x= x/norm(x); % 相机坐标系下的三角形坐标系的x轴单位向量
if abs([0 1 0]*x) < abs([0 0 1]*x)
z= xcross(x,[0; 1; 0]); z= z/norm(z);
y= xcross(z, x); y= y/norm(y);
else
y= xcross([0; 0; 1], x); y= y/norm(y);
z= xcross(x,y); z= z/norm(z);
end
Rx= [x y z]; % 相机坐标系下的三角形坐标系的旋转矩阵
% 计算 c, s, tx, ty, tz
D= zeros(2*n,6);
r= Rx.';
for j= 1:n
ui= xx(1,j); vi= xx(2,j);
xi= XX(1,j); yi= XX(2,j); zi= XX(3,j);
% 下面这个算式应该是生成2nx6的矩阵
D(2*j-1,:)= [-r(2)*yi+ui*(r(8)*yi+r(9)*zi)-r(3)*zi, ...
-r(3)*yi+ui*(r(9)*yi-r(8)*zi)+r(2)*zi, ...
-1, 0, ui, ui*r(7)*xi-r(1)*xi];
D(2*j, :)= [-r(5)*yi+vi*(r(8)*yi+r(9)*zi)-r(6)*zi, ...
-r(6)*yi+vi*(r(9)*yi-r(8)*zi)+r(5)*zi, ...
0, -1, vi, vi*r(7)*xi-r(4)*xi];
end
DTD= D.'*D;
[V D]= eig(DTD);
V1= V(:,1); V1= V1/V1(end);
c= V1(1); s= V1(2); t= V1(3:5); % 当前三角形坐标系的c,s,t
% 通过3d对齐计算相机姿态
xi= XX(1,:); yi= XX(2,:); zi= XX(3,:);
% 旋转至相机坐标系后的三角形物体坐标系,即测量值
XXcs= [r(1)*xi+(r(2)*c+r(3)*s)*yi+(-r(2)*s+r(3)*c)*zi+t(1);
r(4)*xi+(r(5)*c+r(6)*s)*yi+(-r(5)*s+r(6)*c)*zi+t(2);
r(7)*xi+(r(8)*c+r(9)*s)*yi+(-r(8)*s+r(9)*c)*zi+t(3)];
XXc= zeros(size(XXcs));
for j= 1:n
XXc(:,j)= xxv(:,j)*norm(XXcs(:,j)); % xxv之前归一化,现在还原
end
[R t]= calcampose(XXc,XXw); % XXc为测量值,XXw为原物体坐标系的值
% 计算重投影误差
XXc= R*XXw+t*ones(1,n);
xxc= [XXc(1,:)./XXc(3,:); XXc(2,:)./XXc(3,:)];
%r= mean(sqrt(sum((xxc-xx).^2)));
r = norm(xxc-xx,'fro')/n;
res{i}.R= R;
res{i}.t= t;
res{i}.r= r;
end
% 以最小的重投影误差确定相机姿态。
minr= inf;
for i= 1:m
if res{i}.r < minr
minr= res{i}.r;
R= res{i}.R;
t= res{i}.t;
end
end
return
function B = getp3p(l1,l2,A5,C1,C2,D1,D2,D3) % 获取PST方法中的系数矩阵
A1= (D2/D1)^2;
A2= A1*C1^2-C2^2;
A3= l2*A5-l1;
A4= l1*A5-l2;
A6= (D3^2-D1^2-D2^2)/(2*D1^2);
A7= 1-l1^2-l2^2+l1*l2*A5+A6*C1^2;
B= [A6^2-A1*A5^2, 2*(A3*A6-A1*A4*A5), A3^2+2*A6*A7-A1*A4^2-A2*A5^2,...
2*(A3*A7-A2*A4*A5), A7^2-A2*A4^2];
return
function F7= getpoly7(F) % F(x)*F'(x)的7阶系数矩阵
F7= [4*F(1)^2;
7*F(2)*F(1);
6*F(3)*F(1)+3*F(2)^2;
5*F(4)*F(1)+5*F(3)*F(2);
4*F(5)*F(1)+4*F(4)*F(2)+2*F(3)^2;
3*F(5)*F(2)+3*F(4)*F(3);
2*F(5)*F(3)+F(4)^2;
F(5)*F(4)].';
return
function [R2,t2] = calcampose(XXc,XXw) % 计算位姿
n= length(XXc);
X= XXw;
Y= XXc;
K= eye(n)-ones(n,n)/n;
ux= mean(X,2);
uy= mean(Y,2);
sigmx2= mean(sum((X*K).^2));
SXY= Y*K*(X')/n;
[U, D, V]= svd(SXY);
S= eye(3);
if det(SXY) < 0
S(3,3)= -1;
end
R2= U*S*(V');
c2= trace(D*S)/sigmx2;
t2= uy-c2*R2*ux;
X= R2(:,1);
Y= R2(:,2);
Z= R2(:,3);
if norm(xcross(X,Y)-Z) > 2e-2
R2(:,3)= -Z;
end
return
function c = xcross(a,b) % 向量叉乘
c = [a(2)*b(3)-a(3)*b(2);
a(3)*b(1)-a(1)*b(3);
a(1)*b(2)-a(2)*b(1)];
return文章参考:
1.Li S, Xu C. A stable direct solution of perspective-three-point problem[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2011, 25(05): 627-642.
2.Li S, Xu C, Xie M. A robust O (n) solution to the perspective-n-point problem[J]. IEEE transactions on pattern analysis and machine intelligence, 2012, 34(7): 1444-1450.
相关资源:RPnP论文+Matlab代码其中包含epnp,lhm等算法,以及论文原文图片生成代码,各个文件的详解_EPnpmatlab-机器学习文档类资源-CSDN文库