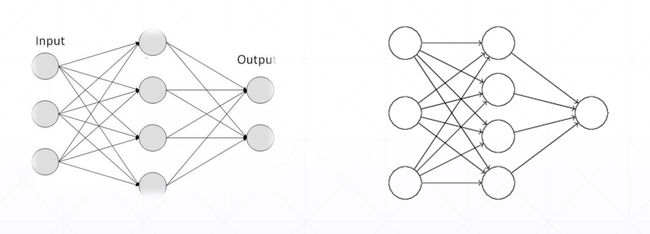
目录
- Outline
- MSE
- Entropy
- Cross Entropy
- Binary Classification
- Single output
- Classification
- Why not MSE?
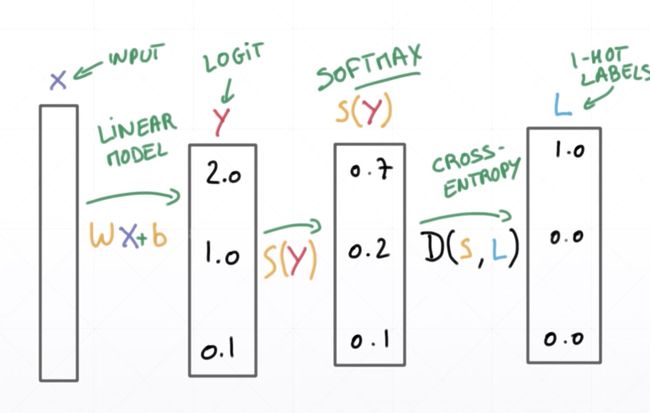
- logits-->CrossEntropy
Outline
MSE
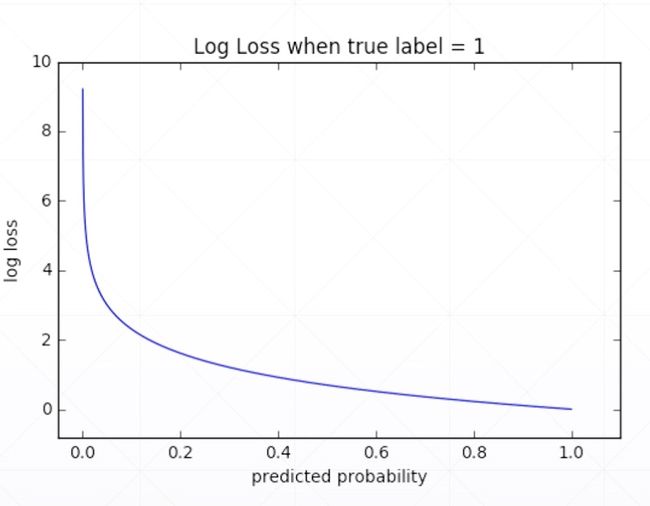
Cross Entropy Loss
Hinge Loss
MSE
\(loss = \frac{1}{N}\sum(y-out)^2\)
\(L_{2-norm} = \sqrt{\sum(y-out)}\)
import tensorflow as tfy = tf.constant([1, 2, 3, 0, 2])
y = tf.one_hot(y, depth=4) # max_label=3种
y = tf.cast(y, dtype=tf.float32)
out = tf.random.normal([5, 4])
outloss1 = tf.reduce_mean(tf.square(y - out))
loss1loss2 = tf.square(tf.norm(y - out)) / (5 * 4)
loss2loss3 = tf.reduce_mean(tf.losses.MSE(y, out))
loss3Entropy
Uncertainty
measure of surprise
lower entropy --> more info.
\[ \text{Entropy} = -\sum_{i}P(i)log\,P(i) \]
a = tf.fill([4], 0.25)
a * tf.math.log(a) / tf.math.log(2.)-tf.reduce_sum(a * tf.math.log(a) / tf.math.log(2.))a = tf.constant([0.1, 0.1, 0.1, 0.7])
-tf.reduce_sum(a * tf.math.log(a) / tf.math.log(2.))a = tf.constant([0.01, 0.01, 0.01, 0.97])
-tf.reduce_sum(a * tf.math.log(a) / tf.math.log(2.))Cross Entropy
\[ H(p,q) = -\sum{p(x)log\,q(x)} \\ H(p,q) = H(p) + D_{KL}(p|q) \]
- for p = q
- Minima: H(p,q) = H(p)
- for P: one-hot encodint
- \(h(p:[0,1,0]) = -1log\,1=0\)
- \(H([0,1,0],[p_0,p_1,p_2]) = 0 + D_{KL}(p|q) = -1log\,q_1\) # p,q即真实值和预测值相等的话交叉熵为0
Binary Classification
- Two cases(第二种格式只需要输出一种情况,节省计算,无意义)
Single output
\[ H(P,Q) = -P(cat)log\,Q(cat) - (1-P(cat))log\,(1-Q(cat)) \\ P(dog) = (1-P(cat)) \\ \]
\[ \begin{aligned} H(P,Q) & = -\sum_{i=(cat,dog)}P(i)log\,Q(i)\\ & = -P(cat)log\,Q(cat) - P(dog)log\,Q(dog)-(ylog(p)+(1-y)log\,(1-p)) \end{aligned} \]
Classification
- \(H([0,1,0],[p_0,p_1,p_2])=0+D_{KL}(p|q) = -1log\,q_1\)
\[ \begin{aligned} & P_1 = [1,0,0,0,0]\\ & Q_1=[0.4,0.3,0.05,0.05,0.2] \end{aligned} \]
\[ \begin{aligned} H(P_1,Q_1) & = -\sum{P_1(i)}log\,Q_1(i) \\ & = -(1log\,0.4+0log\,0.3+0log\,0.05+0log\,0.05+0log\,0.2) \\ & =-log\,0.4 \\ & \approx{0.916} \end{aligned} \]
\[ \begin{aligned} & P_1 = [1,0,0,0,0]\\ & Q_1=[0.98,0.01,0,0,0.01] \end{aligned} \]
\[ \begin{aligned} H(P_1,Q_1) & = -\sum{P_1(i)}log\,Q_1(i) \\ & =-log\,0.98 \\ & \approx{0.02} \end{aligned} \]
tf.losses.categorical_crossentropy([0, 1, 0, 0], [0.25, 0.25, 0.25, 0.25])tf.losses.categorical_crossentropy([0, 1, 0, 0], [0.1, 0.1, 0.8, 0.1])tf.losses.categorical_crossentropy([0, 1, 0, 0], [0.1, 0.7, 0.1, 0.1])tf.losses.categorical_crossentropy([0, 1, 0, 0], [0.01, 0.97, 0.01, 0.01])tf.losses.BinaryCrossentropy()([1],[0.1])tf.losses.binary_crossentropy([1],[0.1])Why not MSE?
- sigmoid + MSE
- gradient vanish
converge slower
- However
- e.g. meta-learning