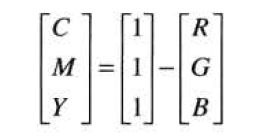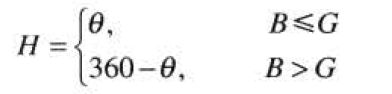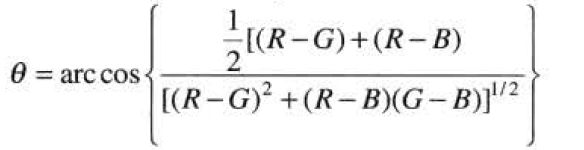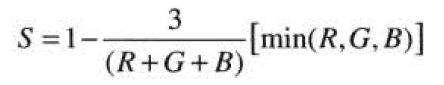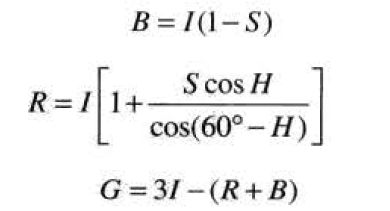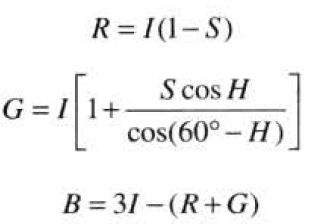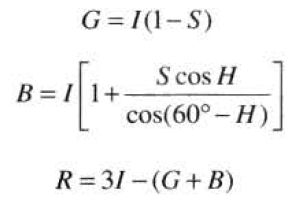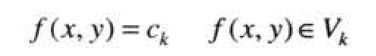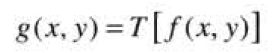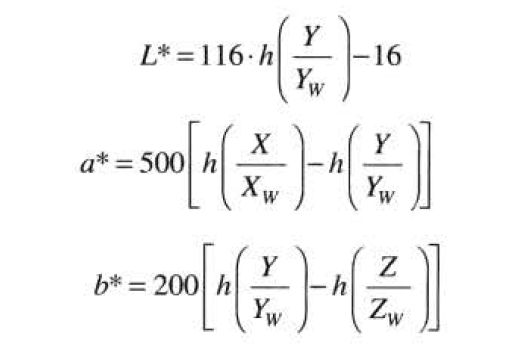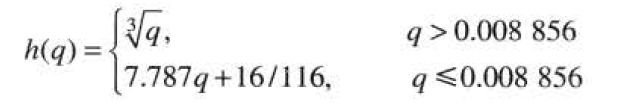数字图像处理第六章——彩色图像处理
目录
引言
一、彩色基础
二、彩色模型
2.1 RGB彩色模型
2.2 CMY和CMYK彩色模型
2.3 HSI彩色模型
三、伪彩色图像处理
3.1 灰度分层
3.2 灰度到彩色的变换
四、彩色变换
编辑色调与色彩校正
五、平滑与锐化
5.1 平滑
5.2 锐化
引言
在图像处理中,彩色的运用受两个主要因素的推动。第一,彩色是--个强有力的描绘子,它常常可简化从场景中提取和识别目标;第二,人可以辨别几千种彩色色调和亮度,但相比之下只能辨别几十种灰度色调。第二个因素在人工图像分析中特别重要。
彩色图像处理可分为两个主要领域:全彩色处理和伪彩色处理.在第一类中,通常要求图像用全彩色传感器获取,如彩色电视摄像机或彩色扫描仪。在第二类中,问题是对一-种特定的单色灰度或灰度范围赋予一种颜色。 到目前为止,多数数字彩色图像处理是在伪彩色层面完成的。但是在过去的十年里彩色传感器和用于处理彩色图像的硬件在价格上变得更加容易接受,因此彩色图像处理技术应用如今十分广泛。
一、彩色基础
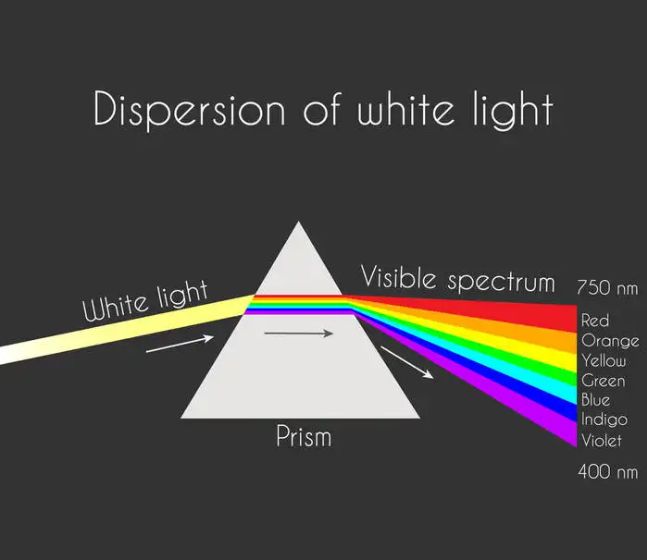
1666年,牛顿发现,当一束太阳光通过一个玻璃棱镜时,会出现由一端为紫色、另一端为红色的连续色谱组成的光束。
如上图所示,色谱由上往下分为红、橙、黄、绿、蓝、靛、紫,在观察色谱时,颜色并不是突变二十平滑的过度到下一个颜色的。基本上,人类和某些其他动物感知一个物体颜色是由物体反射光的性质决定的。
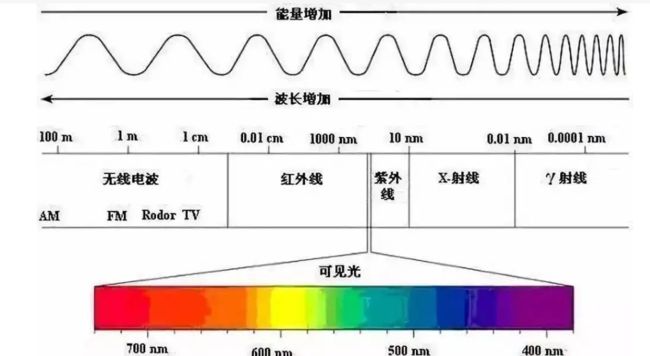
可见光由电磁波谱中相对较窄的频段组成,一个物体反射的光如果在所有可见光波长范围内是平衡的,那么对于观察者而言显示的就是白色的。一个物体反射有限的可见光谱,则物体呈现某种颜色。
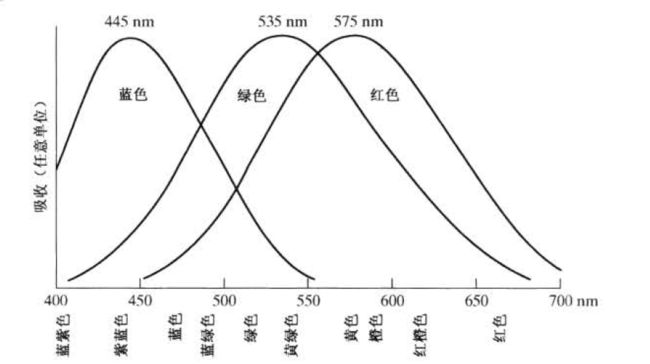
光的特性是彩色科学的核心。如果光是无色的,它的属性就仅仅只是亮度或者数值。无色光就是观察者在黑白电视上看到的光,且是迄今为止我们对图像处理的讨论的隐含分量。对于我们人类而言,由于人眼中的锥状细胞是负责彩色视觉的传感器,其主要可感知3个颜色,包括红色,绿色,和蓝色,这三种颜色又被称为三原色(RGB)。原色相加可以产生二次色,如深红色、青色和黄色,以正确的亮度将三原色或二次色相对应的原色混合就可以产生白光。
通常用以区别不同颜色特性的是亮度、色调和饱和度。亮度具体表达了无色的强度概念.色调是光波混合中与主波长有关的属性。色调表示观察者感知的主要颜色。这样,当我们说一个物体为红色、橙色或黄色时,指的是其色调.饱和度指的是相对的纯净度,或一种颜色混合白光的数量。纯谱色是全饱和的。如深红色(红加白)和淡紫色(紫加白)这样的彩色是欠饱和的,饱和度与所加白光的数量成反比。
色调与饱和度一起称为色度,因此,颜色可用其亮度和色度来表征。形成任何特殊彩色的红、绿、蓝的数量称为三色值,并分别表示为X, Y和Z。这样,一种颜色就可由其三色值系数定义为:![]() ;x,y,z三者相加结果为1。
;x,y,z三者相加结果为1。
二、彩色模型
彩色模型(也称为彩色空间或彩色系统)的目的是在某些标准下用通常可以接受的方式方便地对彩色加以说明。本质上,彩色模型是坐标系统和子空间的说明,其中,位于系统中的每种颜色都由单个点来表示。
2.1 RGB彩色模型
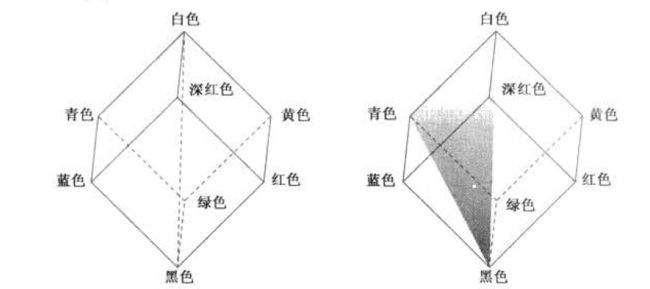
在RGB模型中,每种颜色出现在红、绿、蓝的原色光谱分量中。该模型基于笛卡儿坐标系。所考虑的彩色子空间下图的立方体,图中RGB原色值位于3个角上;二次色青色、深红色和黄色位于另外3个角上,黑色位于原点处,白色位于离原点最远的角上。在该模型中,灰度(RGB值相等的点)沿着连接这两点的直线从黑色延伸到白色。在这一模型中的不同颜色是位于立方体上的或立方体内部的点,且由自原点延伸的向量来定义。
在RGB彩色模型中表示的图像由3个分量图像组成,每种原色一幅分量图像。
当红蓝绿三色分别有一个颜色没有时
temp = np.zeros([512, 512], np.uint8)
x = np.linspace(0, 1, temp.shape[0])
X = np.uint8(normalize(x) * 255)
X = np.tile(X, [512, 1])
y = np.linspace(0, 1, temp.shape[0])
Y = np.uint8(normalize(y) * 255)
Y = np.tile(Y, [512, 1])
# R=0
R_1 = temp
G_1 = X
B_1 = np.rot90(Y)
# G=0
B_2 = np.rot90(Y)
R_2 = np.flip(X)
G_2 = temp
# B=0
B_3 = temp
G_3 = X
R_3 = np.rot90(np.fliplr(Y))
plt.figure(figsize=(20, 5))
plt.gray()
plt.subplot(343), plt.imshow(R_1, ), plt.title('Red Channel'), plt.xticks([]), plt.yticks([])
plt.subplot(342), plt.imshow(G_1, ), plt.title('Green Channel'), plt.xticks([]), plt.yticks([])
plt.subplot(341), plt.imshow(B_1, ), plt.title('Blue Channel'), plt.xticks([]), plt.yticks([])
plt.subplot(347), plt.imshow(R_2, ), plt.title('Red Channel'), plt.xticks([]), plt.yticks([])
plt.subplot(346), plt.imshow(G_2, ), plt.title('Green Channel'), plt.xticks([]), plt.yticks([])
plt.subplot(345), plt.imshow(B_2, ), plt.title('Blue Channel'), plt.xticks([]), plt.yticks([])
plt.subplot(3, 4, 11), plt.imshow(R_3, ), plt.title('Red Channel'), plt.xticks([]), plt.yticks([])
plt.subplot(3, 4, 10), plt.imshow(G_3, ), plt.title('Green Channel'), plt.xticks([]), plt.yticks([])
plt.subplot(3, 4, 9), plt.imshow(B_3, ), plt.title('Blue Channel'), plt.xticks([]), plt.yticks([])
img1 = np.dstack([R_1, G_1, B_1])
img2 = np.dstack([R_2, G_2, B_2])
img3 = np.dstack([R_3, G_3, B_3])
plt.subplot(3, 4, 4), plt.imshow(img1), plt.title('result'), plt.xticks([]), plt.yticks([])
plt.subplot(3, 4, 8), plt.imshow(img2), plt.title('result'), plt.xticks([]), plt.yticks([])
plt.subplot(3, 4, 12), plt.imshow(img3), plt.title('result'), plt.xticks([]), plt.yticks([])
plt.tight_layout()
plt.show()2.2 CMY和CMYK彩色模型
我们知道青色、深红色、黄色是光的二次色,即颜料的原色。大多数在纸上沉积彩色颜料的设备,如彩色打印机和复印机要求输入CMY数据或在内部进行RGB到CMY的转换。
CMY转换到CMKY
def rgb_cmy(img):
img_norm = normalize(img).astype(np.float32)
img_cmy = 1 - img_norm
return img_cmy
def rgb_cmyk(img):
height, width, channel = img.shape
img_cmy = 1 - normalize(img).astype(np.float32)
img_c = np.zeros((height, width), dtype=np.float32)
img_m = np.zeros((height, width), dtype=np.float32)
img_y = np.zeros((height, width), dtype=np.float32)
img_k = np.zeros((height, width), dtype=np.float32)
for h in range(height):
for w in range(width):
temp = img[h, w]
k = min(temp[0], temp[1], temp[2])
c, m, y = img_cmy[h, w]
if k == 1:
img_c[h, w] = 0
img_m[h, w] = 0
img_y[h, w] = 0
img_k[h, w] = 1
else:
img_c[h, w] = (c - k) / (1 - k)
img_m[h, w] = (m - k) / (1 - k)
img_y[h, w] = (y - k) / (1 - k)
img_k[h, w] = k
img_cmyk = np.dstack((img_c, img_m, img_y, img_k))
img_dst = normalize(img_cmyk)
return img_dst
img_ori = cv2.imread('D:\\picture\\test.jpg')
img_ori_norm = normalize(img_ori).astype(np.float32)
img_rgb = img_ori_norm[:, :, ::-1]
plt.figure(figsize=(20, 5))
img_cmy = rgb_cmy(img_rgb)
img_cmyk = rgb_cmyk(img_rgb)
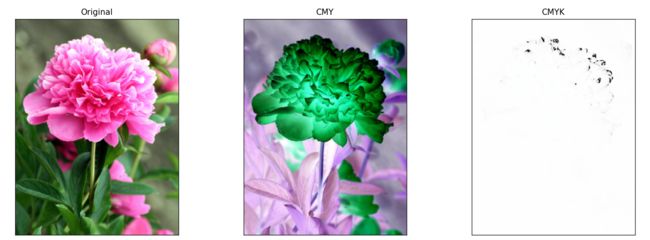
plt.subplot(131), plt.imshow(img_rgb, ), plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.imshow(img_cmy, ), plt.title('CMY'), plt.xticks([]), plt.yticks([])
plt.subplot(133), plt.imshow(img_cmyk, ), plt.title('CMYK'), plt.xticks([]), plt.yticks([])
plt.tight_layout()
plt.show()2.3 HSI彩色模型
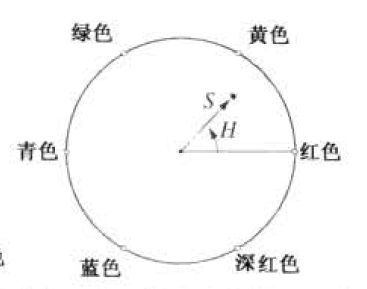
RGB和CMY模型无法很好的适应实际上人类解释的颜色,当人观察一个彩色物体时,一般使用色调、饱和度、亮度来描述它,色调是一个纯色的颜色属性,而饱和度是一种纯色被白光稀释的程度的度量。亮度则是一种主观描述,无法被实际度量。体现了无色的强度概念是描述彩色感觉的关键因子之一。HSI模型可在彩色图像中从携带彩色信息中消去强度分量的影响。因此,HSI模型是开发基于彩色描述的图像处理算法的理想工具,这种彩色描述对于人而言是自然且直观的。
RGB模型和HSI模型的概念关系
从RGB到HSI的彩色转换
对于给定的一幅RGB彩色格式图像,每个RGB像素的H分量可用下式表示:
其中:
饱和度分量为:
强度分量为:
HSI到RGB的的彩色转换
RG扇区(![]() ):当H的值在该扇区中时,RGB分量由以下公式给出:
):当H的值在该扇区中时,RGB分量由以下公式给出:
GB扇区(![]() ):如果给定的H值在该扇区中,则首先从H中减去120°,即:
):如果给定的H值在该扇区中,则首先从H中减去120°,即:
H = H - 120°
RGB分量为:
BR扇区(![]() ):H减去240°
):H减去240°
RGB分量为:
img = cv2.imread('D:\\picture\\tupian.jpg')
img_hsi = cv2.cvtColor(img, cv2.COLOR_BGR2HSV_FULL)
plt.figure(figsize=(20, 5))
plt.subplot(121), plt.imshow(img, ), plt.title('Original')
plt.subplot(122), plt.imshow(img_hsi, ), plt.title('HSI')
plt.tight_layout()
plt.show()三、伪彩色图像处理
伪彩色图像处理是指基于一种指定的规则对灰度值赋以颜色的处理。伪彩色主要应用是人目视观察和解释单幅图像或序列图像中的灰度级事件。
3.1 灰度分层
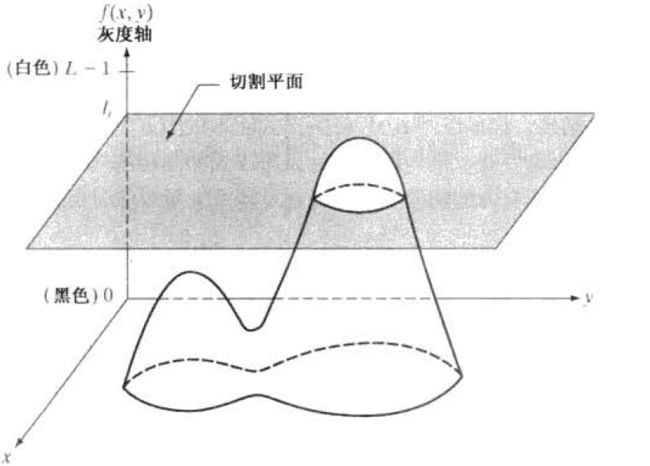
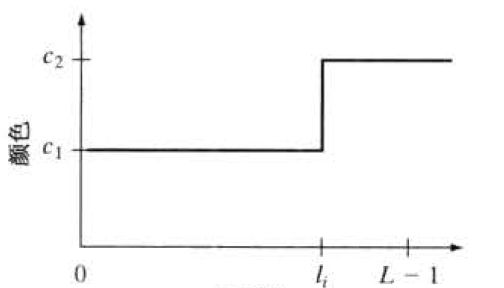
灰度分层和彩色编码技术是伪彩色图像处理的最简单的例子之一。当一幅图像被描述成三维函数,则分层方法可以看成是放置一些平行于该图像的坐标平面的平面,然后,每个平面在相交的区域中“切割”图像函数。
若对上图平面的每一侧赋以不同的颜色,平面上面的任何灰度级的像素将编码成一种彩色。该平面之下的任何像素将编码成另一种颜色。位于平面上的灰度级本身将被任意赋以两种彩色之一。
令[0,L-1]表示灰度级,![]() 代表黑色[f(x,y)=0],并令
代表黑色[f(x,y)=0],并令![]() 代表白色[f(x,y)=L-1],灰度级到彩色赋值根据如下关系进行:
代表白色[f(x,y)=L-1],灰度级到彩色赋值根据如下关系进行:
![]() 是与第k个灰度区间
是与第k个灰度区间![]() 有关的颜色,
有关的颜色,![]() 由位于l=k-1和l=k处的分割平面定义。
由位于l=k-1和l=k处的分割平面定义。
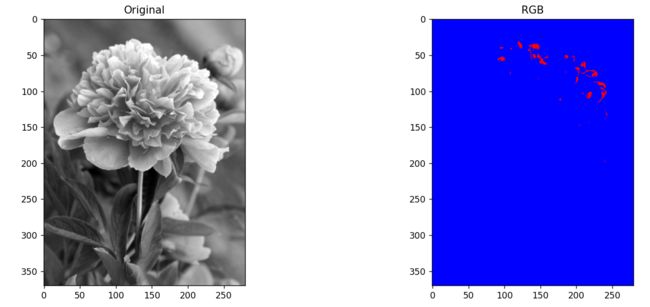
密度分层:
def slice1(img_gray):
img_ori = img_gray / 255.
rows, cols = img_ori.shape[:2]
labels = np.zeros([rows, cols])
for i in range(rows):
for j in range(cols):
if (img_ori[i, j] < 0.125):
labels[i, j] = 0
elif (img_ori[i, j] < 0.25):
labels[i, j] = 0.2
elif (img_ori[i, j] < 0.375):
labels[i, j] = 0.4
elif (img_ori[i, j] < 0.5):
labels[i, j] = 0.5
elif (img_ori[i, j] < 0.625):
labels[i, j] = 0.6
elif (img_ori[i, j] < 0.75):
labels[i, j] = 0.8
elif (img_ori[i, j] < 0.875):
labels[i, j] = 0.9
else:
labels[i, j] = 1
return labels
img = cv2.imread('D:\\picture\\test.jpg', 0)
labels = slice1(img)
labels = np.uint8(labels * 255)
img1 = color.label2rgb(labels)
plt.figure(figsize=(20, 5))
plt.subplot(121), plt.imshow(img, 'gray'), plt.title('Original')
plt.subplot(122), plt.imshow(img1, ), plt.title('RGB')
plt.tight_layout()
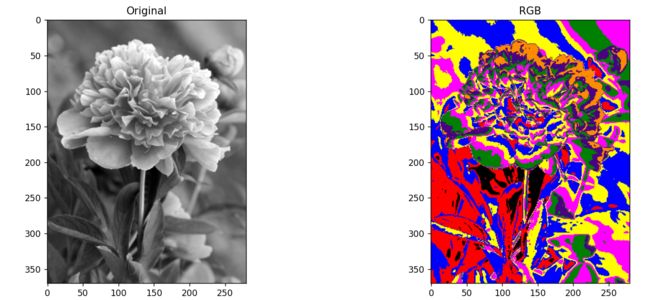
plt.show()彩色编码:
def slice(img_gray):
rows, cols = img_gray.shape[:2]
labels = np.zeros([rows, cols], np.uint8)
for i in range(rows):
for j in range(cols):
if (img_gray[i, j] < 250):
labels[i, j] = 125
else:
labels[i, j] = 100
return labels
img = cv2.imread('D:\\picture\\test.jpg', 0)
labels = slice(img)
img_rgb = color.label2rgb(labels)
plt.figure(figsize=(20, 5))
plt.subplot(121), plt.imshow(img, 'gray'), plt.title('Original')
plt.subplot(122), plt.imshow(img_rgb, ), plt.title('RGB')
plt.tight_layout()
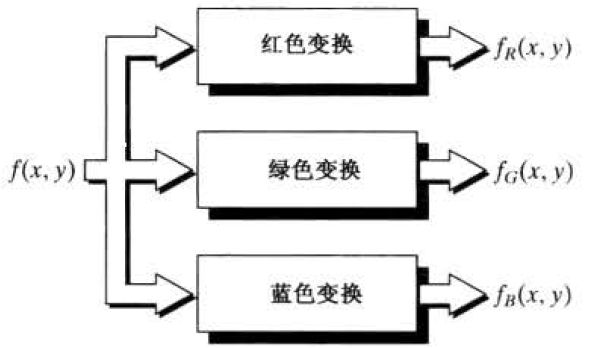
plt.show()3.2 灰度到彩色的变换
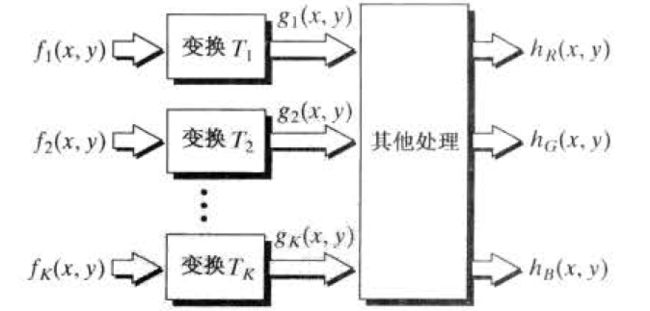
相比于前面讨论的简单分层技术,其他类型的变换更加通用,更能拓宽伪彩色增强结果的范围。
上图便是一种特殊的方法,对任何输入像素的灰度执行3个独立的变换,之后将3个变换结果分别送人彩色电视监视器的红绿蓝通道。
四、彩色变换
彩色变换模型为:
f(x,y)为彩色输入图像,g(x,y)是变换后或处理会的彩色输出图像。T作为一个算子存在。
下面为彩色空间分量的输出:
img_ori = Image.open('D:\\picture\\tupian.jpg')
img_cmyk = img_ori.convert("CMYK")
img_temp = np.array(img_cmyk)
plt.figure(figsize=(10,30))
plt.subplot(541), plt.imshow(img_cmyk), plt.title('Original')
plt.subplot(545), plt.imshow(img_temp[:, :, 0], 'gray'), plt.title('Cyan')
plt.subplot(546), plt.imshow(img_temp[:, :, 1], 'gray'), plt.title('Magenta')
plt.subplot(547), plt.imshow(img_temp[:, :, 2], 'gray'), plt.title('Yellow')
plt.subplot(5, 4, 8), plt.imshow(img_temp[:, :, 3], 'gray'), plt.title('Black')
img_rgb = np.array(img_ori)
plt.subplot(5, 4, 9), plt.imshow(img_rgb[:, :, 0], 'gray'), plt.title('Red')
plt.subplot(5, 4, 10), plt.imshow(img_rgb[:, :, 1], 'gray'), plt.title('Green')
plt.subplot(5, 4, 11), plt.imshow(img_rgb[:, :, 2], 'gray'), plt.title('Blue')
img_hsi = img_ori.convert("HSV")
img_hsi = np.array(img_hsi)
plt.subplot(5, 4, 13), plt.imshow(img_hsi[:, :, 0], 'gray'), plt.title('Hue')
plt.subplot(5, 4, 14), plt.imshow(img_hsi[:, :, 1], 'gray'), plt.title('Saturation')
plt.subplot(5, 4, 15), plt.imshow(img_hsi[:, :, 2], 'gray'), plt.title('Intensity')
plt.tight_layout()
plt.show()
色调与色彩校正
彩色变换可在多数台式计算机上执行,与数字摄像机、平板扫描仪和喷墨打印机相连,个人计算机就变成了数字暗室,允许我们对图像进行色调调整和彩色校正。许多彩色处理系统选择的模型都是CIE L*a*b模型。公式如下:
![]() 是参考白色三激励值下的一种完美的漫反射白色。
是参考白色三激励值下的一种完美的漫反射白色。
def gamma(img, c, gamma):
img = np.array(img).astype(float)
output_img = c * img ** gamma
img_scale = np.uint8((output_img / output_img.max()) * 255)
return img_scale
img_ori = Image.open('D:\\picture\\test.jpg')
img_colour = gamma(img_ori, 1, 1.5)
plt.figure(figsize=(10, 5))
plt.subplot(121), plt.imshow(img_ori), plt.title('Original')
plt.subplot(1, 2, 2), plt.imshow(img_colour), plt.title('Colour Correct')
plt.tight_layout()
plt.show()五、平滑与锐化
5.1 平滑
算术均值滤波法
def arithmentic(image, kernel):
img_h = image.shape[0]
img_w = image.shape[1]
m = kernel.shape[0]
n = kernel.shape[1]
# padding
padding_h = int((m - 1) / 2)
padding_w = int((n - 1) / 2)
image_pad = np.pad(image.copy(), (padding_h, padding_w), mode="constant", constant_values=0)
image_convol = image.copy()
for i in range(padding_h, img_h + padding_h):
for j in range(padding_w, img_w + padding_w):
temp = np.sum(image_pad[i - padding_h:i + padding_h + 1, j - padding_w:j + padding_w + 1] * kernel)
image_convol[i - padding_h][j - padding_w] = 1 / (m * n) * temp
image_convol = np.uint8(normalize(image_convol) * 255)
return image_convol
img_ori = cv2.imread('D:\\picture\\test.jpg')
img_ori = img_ori[:, :, ::-1]
img_rgb = np.array(img_ori)
img_hsi = cv2.cvtColor(np.array(img_ori), cv2.COLOR_RGB2HSV)
img_hsi = np.array(img_hsi)
mean_kernal = np.ones([5, 5])
mean_kernal = mean_kernal / (mean_kernal.size)
img_rgb1 = np.zeros(img_rgb.shape, np.uint8)
for i in range(3):
img_temp = img_rgb[:, :, i]
img_dst = arithmentic(img_temp, kernel=mean_kernal)
img_rgb1[:, :, i] = img_dst
img_hsi1 = np.zeros(img_rgb.shape, np.uint8)
for i in range(3):
if i == 2:
img_temp = img_hsi[:, :, i]
img_dst = arithmentic(img_temp, kernel=mean_kernal)
img_hsi1[:, :, i] = img_dst
else:
img_hsi1[:, :, i] = img_hsi[:, :, i]
img_hsi_rgb = cv2.cvtColor(img_hsi1, cv2.COLOR_HSV2RGB)
plt.figure(figsize=(15, 5))
plt.subplot(1, 2, 1), plt.imshow(img_rgb1), plt.title('RGB')
plt.subplot(1, 2, 2), plt.imshow(img_hsi_rgb), plt.title('HSI RGB')
plt.tight_layout()
plt.show()
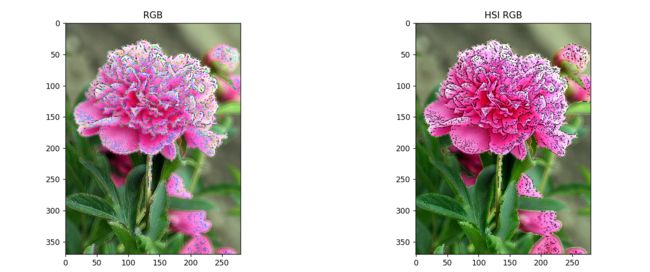
5.2 锐化
考虑采用拉普拉斯方法来处理图像锐化问题,之前我们有学过拉普拉斯算子,在RGB彩色系统中,向量的拉普拉斯变换为:
可以通过分别计算每一个分量图像的拉普拉斯来计算全彩色图像的拉普拉斯。
def la(img_gray):
kernel_laplacian = np.array((
[1, 1, 1],
[1, -8, 1],
[1, 1, 1]), np.int8)
imgkernel_laplacian = cv2.filter2D(img_gray, -1, kernel_laplacian)
laplacian_img = np.uint8(normalize(img_gray + imgkernel_laplacian) * 255)
return laplacian_img
img_ori = cv2.imread('D:\\picture\\test.jpg')
img_ori = img_ori[:, :, ::-1]
img_rgb = np.array(img_ori)
img_hsi = cv2.cvtColor(np.array(img_ori), cv2.COLOR_RGB2HSV)
img_hsi = np.array(img_hsi)
img_rgb_new = np.zeros(img_rgb.shape, np.uint8)
for i in range(3): # 计算每个分量的拉普拉斯
img_temp = img_rgb[:, :, i]
img_dst = la(img_temp)
img_rgb_new[:, :, i] = img_dst
img_hsi1 = np.zeros(img_rgb.shape, np.uint8)
for i in range(3):
if i == 2:
img_temp = img_hsi[:, :, i]
img_dst = la(img_temp)
img_hsi1[:, :, i] = img_dst
else:
img_hsi1[:, :, i] = img_hsi[:, :, i]
img_hsi_rgb = cv2.cvtColor(img_hsi1, cv2.COLOR_HSV2RGB)
plt.figure(figsize=(15, 5))
plt.subplot(1, 2, 1), plt.imshow(img_rgb_new), plt.title('RGB')
plt.subplot(1, 2, 2), plt.imshow(img_hsi_rgb), plt.title('HSI RGB')
plt.tight_layout()
plt.show()