多元统计分析及R语言建模（王斌会）第三第四章答案
3)要了解学校毕业生起始工资的变化是否能用学生的平均成绩点数(GPA)和毕业时的年龄来解释。表4-7为某学校办公室提供的样本数据。
表4-7某学校学生起始工资、GPA及年龄数据
| GPA |
年龄 |
起始工资 |
| 2.95 3.40 3.20 3.10 3.05 2.75 3.15 2.75 |
22 23 27 25 23 28 26 26 |
25 500 28 100 28 200 25 000 22 700 22 500 26 000 23 800 |
（1）试做回归模型并解释各系数;
> library(openxlsx)
> e4.3 = read.xlsx('E:/mvexer5.xlsx','E4.3')
> fm = lm(起始工资~ GPA + 年龄,data = e4.3) #多元线性回归模型
> fm
在Rstudio中运行结果如下
图3.1建立回归模型
由运行结果知多元线性回归函数为：
起始工资 = -5213.1 + 8508.8*GPA + 181.6*年龄
解释：在GPA不变的情况下，年龄每增加一个单位，起始工资就增加181.6个单位；
在年龄不变的情况下，GPA每增加一个单位，起始工资增加8508.8个单位。
- 确定学生的GPA和年龄是否能真正用来解释起始工资样本的变化;
> summary(fm) #检验回归系数
> (R4.3 = summary(fm) $ r.sq) #显示多元线性回归模型决定系数
> (R4.4.3 = sqrt(R4.3)) #显示多元数据复相关系数
在Rstudio中运行结果如下：
图3.2检验回归模型
R2= 
Multiple R-squared=0.6677不接近1,说明回归方程拟合度低，学生的GPA和年龄不能真正用来解释起始工资样本的变化
（3）预测某GPA为3.00,年龄为24岁的毕业生的起始工资。
> predict(fm,newdata = data.frame(GPA = 3,年龄 = 24))
在R语言中运行结果如下：
图3.3预测起始工资
4)研究货运总量y（万吨）与工业总产值x1（亿元）、农业总产值x2（亿元）、居民非商品支出x3(亿元)的关系。有关数据见表4-8
- 计算y,x1,x2,x3的相关系数矩阵并绘制矩阵散点图
> library(openxlsx)
> e4.4 = read.xlsx('E:/mvexer5.xlsx',sheet = 'E4.4')
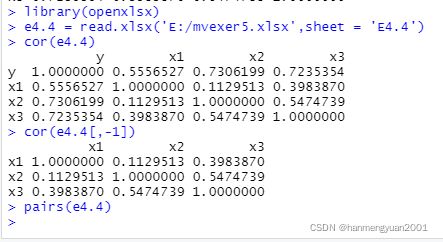
> cor(e4.4) #y,x1,x2,x3的相关系数矩阵
> cor(e4.4[,-1]) #去除y后的相关系数矩阵
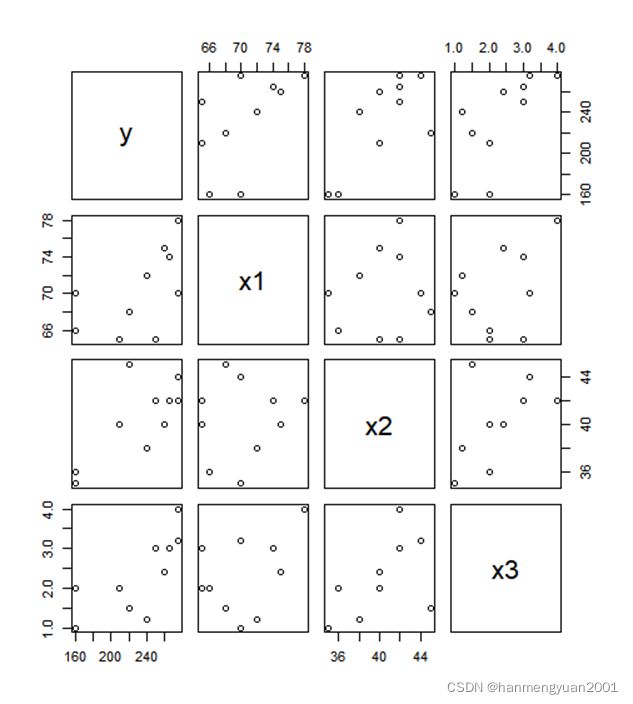
> pairs(e4.4) #绘制矩阵散列图
用Rstudio运行如下：
图4.1相关系数矩阵
图4.2矩阵散列图
（2）求y关于x1,x2,x3的多元线性回归方程
> fm <- lm(y ~ x1 + x2 + x3,data = e4.4)
> summary(fm)
在Rstudio中运行结果如下：
图4.3多元线性回归方程
（6）使用逐步回归分析的逐步筛选方法获得一个最优的回归模型
> fm.step = step(fm,direction = 'both') #逐步筛选法变量选择结果
在Rstudio中运行结果如下：
图4.4逐步筛选回归模型
3)某银行从历史贷款客户中随机抽取16个样本，根据设计的指标体系分别计算他们的“商业信用支持度”(x1)和“市场竞争地位等级”（x2),类别变量G中，1代表贷款成功，2代表贷款失败。数据如表5-11所示
（1）为了给正确贷款提供决策支持，请建立Logistic模型进行分析；
> library(openxlsx)
> e5.3 = read.xlsx('E:/mvexer5.xlsx',sheet = 'E5.3')
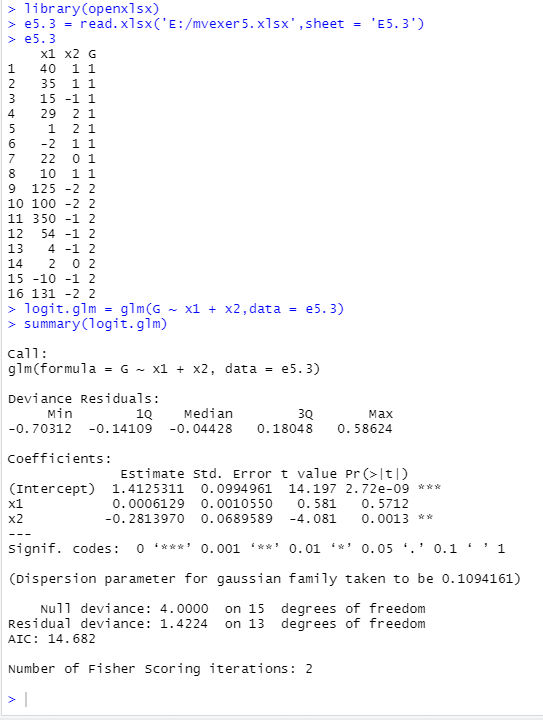
> logit.glm = glm(G ~ x1 + x2,data = e5.3) #建立Logistic模型
> summary(logit.glm)
在Rstudio中运行结果如下：
图5.1Logistic模型分析
由运行结果知logistic拟合的模型x1的P>0.05，x2的P<0.05，说明有影响
（2）根据建立的模型，判定是否给某用户（x1 = 131,x2 = -2）提供贷款。
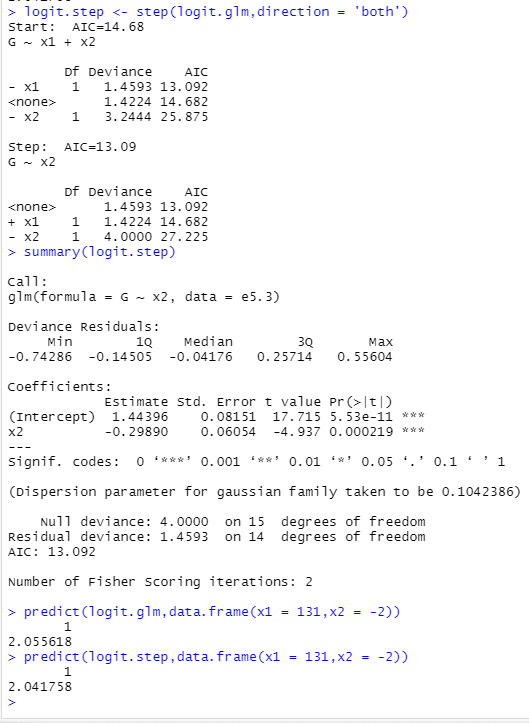
> logit.step <- step(logit.glm,direction = 'both') #逐步筛选法变量选择
> summary(logit.step)
> predict(logit.glm,data.frame(x1 = 131,x2 = -2))
> predict(logit.step,data.frame(x1 = 131,x2 = -2))
在Rstudio中运行结果如下：
图5.2判定是否提供贷款
由运行结果知，预测值为2，表示贷款失败，不会给用户（x1 = 131,x2 = -2）提供贷款。