【注意力机制集锦2】BAM&SGE&DAN原文、结构、源码详解
注意力机制集锦2
前面我们已经系统介绍了注意力机制的概念、分类及近年来的发展概况,传送门:
【注意力机制引言】
并且对注意力机制中的通道注意力机制SENet、SKNet、CBAM进行了介绍,传送门:
【通道注意力机制系列一】
在这篇文章中,我们将继续沿着视觉注意力机制的发展脉络,针对注意力机制中比较著名的几种算法进行原文、结构、源码的解读。Talk is cheap,let’s view the code.
1 BAM:Bottleneck Attention Module
原文链接:https://arxiv.org/pdf/1807.06514.pdf
源码链接:https://github.com/Jongchan/attention-module

这篇文章由CBAM原班人马打造,算是CBAM的姊妹算法,机制原理其实CBAM非常相似。上图中作者将BAM放在了Resnet网络中每个stage之间,有趣的是,通过可视化我们可以看到多层BAM形成了一个分层的注意力机制,这有点像人类的感知机制。说明BAM能够在每个stage之间消除像背景语义特征这样的低层次特征,并逐渐聚焦于高层次语义信息,如图中的单身喵的聚焦过程。
1.1 BAM解读
对于输入到网络中的特征图,BAM会分别基于channel和spatial这两个通路进行注意力权重的计算,将两个通路中
得到的特征向量相加后组成新的注意力权重,最后使用sigmoid函数进行激活。其中比较重要的三点:
(1)BAM整体作为一个残差结构使用,所以不像之前的模块直接乘到特征图中,原文对其数学定义如公式(1)所示。
(2)CBAM使用串接的方式将channel和spatial层次的注意力权重进行融合,而BAM使用并联的方式将二者进行分离,并且直接将二者得到的注意力权重进行相加,其数学定义如公式(2)所示。
(3)Channel层次的注意力通路得到的权重尺寸与Spatial层次的权重尺寸不同怎么办?其实不仅是这里相加的时候维度不一,Spatial内部权重图融合的时候也是有维度不一的情况。作者在文章中并没有过多讨论这个问题,但是源码中作者仅仅使用广播机制将输出映射到与输入相同的尺寸大小。

1.1.1 Channel attention branch

与CBAM中的通道注意力机制不同,BAM中仅使用了全局平均池化生成Channel维度的特征,并通过两层全连接层FC来学习不同的输入通道的权重,最终得到Cx1x1尺寸的通道权重M_c。数学定义如公式(3)所示:
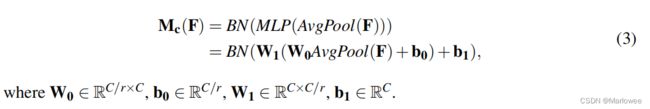
从公式中可以看到,对于两层全连接层,作者在学习权重的过程中使用的SENet中提到的衰减参数r进行降维,再重新映射回原来的维度大小,最后对特征向量进行BatchNorm。可以说,BAM减少了通道注意力这部分的网络内容,而把更多精力放到了空间注意力上。
1.1.2 Spatial attention branch

作者团队本小节开头提到了设计这部分网络的初衷:大的感受野能够促进网络有效地利用上下文信息,所以作者团队引入空洞卷积(又名膨胀卷积、扩张卷积)来高效率地扩大感受野。
对于输入特征图F,网络首先使用1x1的卷积对其进行通道降维,具体降至几通道由衰减参数r决定(大家可以回想一下CBAM是如何降维的,做一下对比);然后,通过重复的扩张卷积操作对特征图的空间权重进行学习,文中示意是使用2层kernel_size=3,dilation_val=4的卷积层来实现的,大家也可以自行使用不同层数、不同空洞率的卷积操作来进行复现;最后再使用1x1的卷积操作将特征权重的通道数降为1。其数学定义如公式(4)所示。
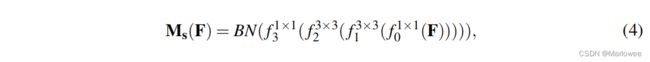
1.1.3 One more thing
最后说一下自己在看paper\code时候的几点想法:
(1)首先,对于channel和spatial两个通路上得到的特征权重,作者不加区分地使用广播机制将其映射到原始输入的尺寸,这种方式是否利于权重的学习呢?
(2)其次,在spatial这个通路,作者通过下采样的卷积层学习空间权重。如果作者是想通过空洞卷积来进行空间权重的学习,为何不用特征图的H和W不变的卷积操作,这样下采样完成后还要再通过广播进行维度复原,这让人很难理解下采样的动机。
(3)最后,也是在spatial这个通路,网络最后将学习完成后将通道数压缩为1,但是随后的channel+spatial操作又重新把通道数进行广播,是否多余? 写完之后想了想,更多层的MLP操作可能会更多地学习特征间的非线性特征,达到更好的拟合效果?
1.2 代码解读
BAM中的两个通路主要是用模块序列来实现的,所以读代码的时候要先看自己设置的超参数r和layer_num,然后前向传播结束时返回的都是通过.expand_as(x)(这个操作比较重要,大家自行查阅)操作广播后的特征图。内部具体的细节按照上述的解读就能理解,不多赘述。
import torch
from torch import nn
from torch.nn import init
class Flatten(nn.Module):
def forward(self,x):
return x.view(x.shape[0],-1)
class ChannelAttention(nn.Module):
def __init__(self,channel,reduction=16,num_layers=3):
super().__init__()
self.avgpool=nn.AdaptiveAvgPool2d(1)
gate_channels=[channel]
gate_channels+=[channel//reduction]*num_layers
gate_channels+=[channel]
self.ca=nn.Sequential()
self.ca.add_module('flatten',Flatten())# 特征图扁平化
for i in range(len(gate_channels)-2):# 构造全连接层
self.ca.add_module('fc%d'%i,nn.Linear(gate_channels[i],gate_channels[i+1]))
self.ca.add_module('bn%d'%i,nn.BatchNorm1d(gate_channels[i+1]))
self.ca.add_module('relu%d'%i,nn.ReLU())
self.ca.add_module('last_fc',nn.Linear(gate_channels[-2],gate_channels[-1]))
def forward(self, x) :
res=self.avgpool(x)
res=self.ca(res)
return res.unsqueeze(-1).unsqueeze(-1).expand_as(x)
class SpatialAttention(nn.Module):
def __init__(self,channel,reduction=16,num_layers=3,dia_val=2):
super().__init__()
self.sa=nn.Sequential()
self.sa.add_module('conv_reduce1',nn.Conv2d(kernel_size=1,in_channels=channel,out_channels=channel//reduction))
self.sa.add_module('bn_reduce1',nn.BatchNorm2d(channel//reduction))
self.sa.add_module('relu_reduce1',nn.ReLU())
for i in range(num_layers):
self.sa.add_module('conv_%d'%i,nn.Conv2d(kernel_size=3,in_channels=channel//reduction,out_channels=channel//reduction,padding=1,dilation=dia_val))
self.sa.add_module('bn_%d'%i,nn.BatchNorm2d(channel//reduction))
self.sa.add_module('relu_%d'%i,nn.ReLU())
self.sa.add_module('last_conv',nn.Conv2d(channel//reduction,1,kernel_size=1))
def forward(self, x) :
res=self.sa(x)
return res.expand_as(x)
class BAMBlock(nn.Module):
def __init__(self, channel=512,reduction=16,dia_val=2):
super().__init__()
self.ca=ChannelAttention(channel=channel,reduction=reduction)
self.sa=SpatialAttention(channel=channel,reduction=reduction,dia_val=dia_val)
self.sigmoid=nn.Sigmoid()
def init_weights(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
init.kaiming_normal_(m.weight, mode='fan_out')
if m.bias is not None:
init.constant_(m.bias, 0)
elif isinstance(m, nn.BatchNorm2d):
init.constant_(m.weight, 1)
init.constant_(m.bias, 0)
elif isinstance(m, nn.Linear):
init.normal_(m.weight, std=0.001)
if m.bias is not None:
init.constant_(m.bias, 0)
def forward(self, x):
b, c, _, _ = x.size()
sa_out=self.sa(x)
ca_out=self.ca(x)
weight=self.sigmoid(sa_out+ca_out)
out=(1+weight)*x
return out
if __name__ == '__main__':
input=torch.randn(50,512,7,7)
bam = BAMBlock(channel=512,reduction=16,dia_val=2)
output=bam(input)
print(output.shape)
2 DANet:Dual Attention Network
原文链接:https://arxiv.org/abs/1809.02983
源码链接:https://github.com/junfu1115/DANet
DANet是基于语义分割任务提出的一种注意力机制,摒弃了之前的encoder-decoder结构,使用空洞卷积+注意力机制,在特征图下采样率不高的情况下,分别在空间和通道两个层次上捕捉远距离的上下文信息,在2019年的多项比赛中取得了SOFT的成绩。
2.1 DANet解读
由于卷积运算产生的感受野是局部的,可能一辆车在不同的感受野中所表现的局部特征就不一样,即具有相同标签的像素对应的特征可能会有一定的差异,这些差异导致的类内差异性,从而影响识别精度。为了解决这个问题,作者通过在网络中建立特征与注意机制之间的关联来探索全局上下文信息,进而提升场景分割的特征表达能力。
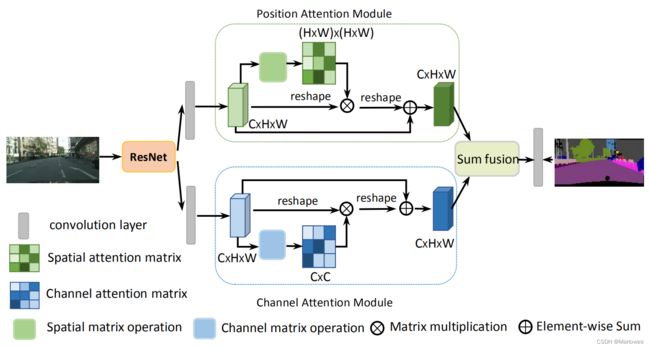
DANet结构原理如上图所示,具体流程:
(1)对于输入的图片,DANet使用去掉了将采样操作的ResNet作为骨架网络进行特征提取,并在ResNet最后两个模块中使用了空洞卷积,所以最终得到的特征图扩大到了原图的1/8,这种改进在不额外添加参数的情况下保留更多的底层细节;
(2)将从骨架网络中得到的特征图用卷积操作降维(ResNet之后的两个灰色矩形),得到输入Position Attention Module和Channel Attention Module的特征,通过上述两个模块中提取像素间和通道间的关联信息。
(3)将两个模块中的输出进行融合,以获得更好的特征表示,用于像素级的预测。
2.1.1 Position Attention Module

上图是位置注意力模块的结构细节,原始输入A经过三个相同的卷积操作得到B、C、D。(我怎么觉得这里的将A映射到BCD的卷积操作跟Transformer中的原始输入经过映射变为QKV那么像呢?????)
对于输入B和C,其原始尺寸为ChannelxHxW,网络将其从三维特征reshape到二维特征,尺寸变为ChannelxN(N=HxW);但是对于B而言,不仅要reshape,还要再transpose(转置),否则两个相同的非方阵无法进行矩阵乘法。所以输入B最终变成NxChannel的特征,C最终变为ChannelxN的特征。随后二者通过矩阵乘法并经过softmax激活得到上图中的S,其尺寸为NxN。具体数学定义如下图所示:

A同样经过卷积操作得到了D,对D进行reshape操作得到尺寸为ChannelxN的特征,然后把尺寸为NxN的特征S与转置后的D(此时D的尺寸为NxChannel)做矩阵乘法,最终得到的特征向量再reshape到ChannelxHxW的尺寸(说实话我也被作者的操作绕得不行,这里其实不用太追究细节)
最后,将A和经过一系列操作的D相加进行信息融合,得到作者所言的关联了远距离上下文位置信息的特征图E!计算E的数学公式如下图所示:
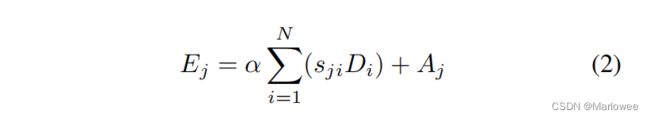
Q:为什么这么做?
其实通过ABCD四个操作我们就可以看出:每个位置的结果特征E是所有位置的特征(BCD系列操作的结果)与原始特征A的加权和。因此,它具有宏观的、全局的语义视图,能够根据位置特征图有选择地聚合语境,实现了相似的语义特征相互受益,从而提高了类内的紧凑性和语义的一致性。
2.1.2 Channel Attention Module

Channel Attention Module采取的策略类似位置注意力,不同的是没有通过中间的卷积映射得到BCD,而是直接基于A进行特征提取,具体细节结合位置注意力机制和上图能够很容易理解,这里我就不赘述了。
2.2 代码解读
我去看了一下代码,对于pa中的卷积映射那一部分,作者好像真的借鉴了Transformer,因为他直接将三个特征图命名为q、k、v了!说实话这部分内容真的太绕了,代码我也没看太看明白,所以这里只贴出了主体代码,具体细节先留个坑,有时间再填…
class PositionAttentionModule(nn.Module):
def __init__(self,d_model=512,kernel_size=3,H=7,W=7):
super().__init__()
self.cnn=nn.Conv2d(d_model,d_model,kernel_size=kernel_size,padding=(kernel_size-1)//2)
self.pa=ScaledDotProductAttention(d_model,d_k=d_model,d_v=d_model,h=1)
def forward(self,x):
bs,c,h,w=x.shape
y=self.cnn(x)
y=y.view(bs,c,-1).permute(0,2,1) #bs,h*w,c
y=self.pa(y,y,y) #bs,h*w,c
return y
class ChannelAttentionModule(nn.Module):
def __init__(self,d_model=512,kernel_size=3,H=7,W=7):
super().__init__()
self.cnn=nn.Conv2d(d_model,d_model,kernel_size=kernel_size,padding=(kernel_size-1)//2)
self.pa=SimplifiedScaledDotProductAttention(H*W,h=1)
def forward(self,x):
bs,c,h,w=x.shape
y=self.cnn(x)
y=y.view(bs,c,-1) #bs,c,h*w
y=self.pa(y,y,y) #bs,c,h*w
return y
class DAModule(nn.Module):
def __init__(self,d_model=512,kernel_size=3,H=7,W=7):
super().__init__()
self.position_attention_module=PositionAttentionModule(d_model=512,kernel_size=3,H=7,W=7)
self.channel_attention_module=ChannelAttentionModule(d_model=512,kernel_size=3,H=7,W=7)
def forward(self,input):
bs,c,h,w=input.shape
p_out=self.position_attention_module(input)
c_out=self.channel_attention_module(input)
p_out=p_out.permute(0,2,1).view(bs,c,h,w)
c_out=c_out.view(bs,c,h,w)
return p_out+c_out
if __name__ == '__main__':
input=torch.randn(50,512,7,7)
danet=DAModule(d_model=512,kernel_size=3,H=7,W=7)
print(danet(input).shape)
最后贴一句文学回忆录中我最喜欢的片段:
