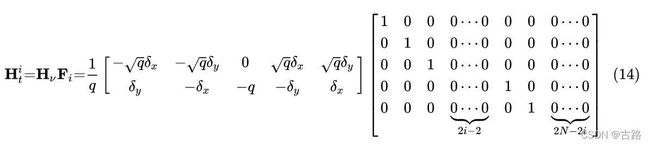EKF-SLAM原理推导
EKF-SLAM
-
- 0.引言
- 1. 运动模型
-
- 1.1.里程计模型
- 1.2.运动更新
- 2.测量模型
- 3.地图更新
-
- 3.1.新地图点的协方差
- 3.2 新地图点与原状态之间的协方差
- 4.数据关联
- 5.demo
0.引言
-
参考链接。基本是基于概率机器人进行实现的,是一个很好的学习材料。此博客只是个人学习记录。
-
ref01.第五课 EKF SLAM
-
ref02.EKF_SLAM实践。特别好的一篇文章。
A l g o r i t h m E x t e n d e d K a l m a n f i l t e r ( μ t − 1 , Σ t − 1 , u t , z t ) Algorithm Extended Kalman filter \left(\mu_{t-1}, \Sigma_{t-1}, u_{t}, z_{t}\right) AlgorithmExtendedKalmanfilter(μt−1,Σt−1,ut,zt) μ ˉ t = g ( u t , μ t − 1 ) Σ ˉ t = G t Σ t − 1 G t T + W k R t W k T K t = Σ ˉ t H t T ( H t Σ ˉ t H t T + V k Q t V k T ) − 1 μ t = μ ˉ t + K t ( z t − h ( μ ˉ t ) ) Σ t = ( I − K t H t ) Σ ˉ t \begin{aligned} &\bar{\mu}_{t}=g\left(u_{t}, \mu_{t-1}\right) \\ &\bar{\Sigma}_{t}=G_{t} \Sigma_{t-1} G_{t}^{T}+W_kR_{t}W_k^{T} \\ &K_{t}=\bar{\Sigma}_{t} H_{t}^{T}\left(H_{t} \bar{\Sigma}_{t} H_{t}^{T}+V_kQ_{t}V_k^{T}\right)^{-1} \\ &\mu_{t}=\bar{\mu}_{t}+K_{t}\left(z_{t}-h\left(\bar{\mu}_{t}\right)\right) \\ &\Sigma_{t}=\left(I-K_{t} H_{t}\right) \bar{\Sigma}_{t} \end{aligned} μˉt=g(ut,μt−1)Σˉt=GtΣt−1GtT+WkRtWkTKt=ΣˉtHtT(HtΣˉtHtT+VkQtVkT)−1μt=μˉt+Kt(zt−h(μˉt))Σt=(I−KtHt)Σˉt
PR书上的公式有点不完善,我加了一点。然后照着EKF公式推一下. 状态量为: X = [ x y θ m x , 1 m y , 1 m x , 2 m y , 2 ⋯ m x , N m y , N ] T \mathbf{X}=\left[\begin{array}{llllllllll} x & y & \theta & m_{x, 1} & m_{y, 1} & m_{x, 2} & m_{y, 2} & \cdots & m_{x, N} & m_{y, N} \end{array}\right]^{T} X=[xyθmx,1my,1mx,2my,2⋯mx,Nmy,N]T
代码中状态量,初始化时只有机器人位姿,后续在增广添加marker:
/* 初始时刻机器人位姿为0,绝对准确, 协方差为0 */
mu_.resize(3, 1);
mu_.setZero();
sigma_.resize(3, 3);
sigma_.setZero();
前3项是机器人位姿,后2N项是 N个路标点的位置。
1. 运动模型
g ( u t , x t − 1 ) ≈ g ( u t , μ t − 1 ) + g ′ ( u t , μ t − 1 ) ⏟ = : G t ( x t − 1 − μ t − 1 ) = g ( u t , μ t − 1 ) + G t ( x t − 1 − μ t − 1 ) \begin{aligned} g\left(\boldsymbol{u}_{t}, \boldsymbol{x}_{t-1}\right) & \approx g\left(\boldsymbol{u}_{t}, \boldsymbol{\mu}_{t-1}\right)+\underbrace{g^{\prime}\left(\boldsymbol{u}_{t}, \boldsymbol{\mu}_{t-1}\right)}_{=: G_{t}}\left(\boldsymbol{x}_{t-1}-\boldsymbol{\mu}_{t-1}\right) \\ &=g\left(\boldsymbol{u}_{t}, \boldsymbol{\mu}_{t-1}\right)+G_{t}\left(\boldsymbol{x}_{t-1}-\boldsymbol{\mu}_{t-1}\right) \end{aligned} g(ut,xt−1)≈g(ut,μt−1)+=:Gt g′(ut,μt−1)(xt−1−μt−1)=g(ut,μt−1)+Gt(xt−1−μt−1)
运动模型需要确定的量: 运动模型 g ( ∗ ) g(*) g(∗) 、控制输入 u t u_t ut 、 g ( ∗ ) g(*) g(∗) 对 状态量的 Jacobian 矩阵 G t G_t Gt 、 g ( ∗ ) g(*) g(∗) 对过程噪声的 Jacobian 矩阵 W k W_k Wk、 噪声协方差矩阵 R t R_t Rt.
1.1.里程计模型
[ x y θ ] t = [ x y θ ] t − 1 + [ Δ s cos ( θ t − 1 + Δ θ / 2 ) Δ s sin ( θ t − 1 + Δ θ / 2 ) Δ θ ] \left[\begin{array}{l} x \\ y \\ \theta \end{array}\right]_{t}=\left[\begin{array}{l} x \\ y \\ \theta \end{array}\right]_{t-1}+\left[\begin{array}{c} \Delta s \cos (\theta_{t-1}+\Delta \theta / 2) \\ \Delta s \sin (\theta_{t-1}+\Delta \theta / 2) \\ \Delta \theta \end{array}\right] ⎣⎡xyθ⎦⎤t=⎣⎡xyθ⎦⎤t−1+⎣⎡Δscos(θt−1+Δθ/2)Δssin(θt−1+Δθ/2)Δθ⎦⎤ { Δ θ = Δ s r − Δ s l b Δ s = Δ s r + Δ s l 2 , Δ s l / r = k l / r ⋅ Δ e l / r (1) \left\{\begin{array}{l} \Delta \theta=\frac{\Delta s_{r}-\Delta s_{l}}{b} \\ \Delta s=\frac{\Delta s_{r}+\Delta s_{l}}{2} \end{array}, \Delta s_{l / r}=k_{l / r} \cdot \Delta e_{l / r}\right.\tag{1} {Δθ=bΔsr−ΔslΔs=2Δsr+Δsl,Δsl/r=kl/r⋅Δel/r(1) Δ s l / r ∼ N ( Δ s l / r ^ , ∥ k Δ s l / r ^ ∥ 2 ) \Delta s_{l / r} \sim N\left(\widehat{\Delta s_{l / r}}, \quad\left\|k \widehat{\Delta s_{l / r}}\right\|^{2}\right) Δsl/r∼N(Δsl/r ,∥∥∥kΔsl/r ∥∥∥2)
原文公式(1)中最后一列 θ \theta θ 应该是 θ t − 1 \theta_{t-1} θt−1 。 k l / r k_{l / r} kl/r为左右轮系数,把编码器增量 Δ e l / r \Delta e_{l/r} Δel/r转化为左右轮的位移, b b b 是轮间距。公式(1)对应EKF公式(1)
double tmp_th = mu_(2,0) + 0.5 * delta_theta;
double cos_tmp_th = cos( tmp_th );
double sin_tmp_th = sin(tmp_th);
mu_(0, 0) += delta_s * cos_tmp_th;
mu_(1, 0) += delta_s * sin_tmp_th;
mu_(2, 0) += delta_theta;
normAngle(mu_(2, 0)); //norm
左右轮位移的增量 Δ s l / r \Delta s_{l/r} Δsl/r服从高斯分布,均值就是编码器计算出的位移增量,标准差与增量大小成正比。如果t-1时刻机器人位姿的协方差为 Σ ξ , t − 1 \Sigma_{\xi, t-1} Σξ,t−1,控制的协方差也就是左右轮位移增量的协方差为 Σ u \Sigma_{u} Σu,那么机器人位姿在t时刻的协方差就是:
Σ ˉ ξ , t = G ξ Σ ξ , t − 1 G ξ T + G u ′ Σ u G ′ u T (2) \bar \mathbf{\Sigma}_{\xi, t}=\mathbf{G}_{\xi} \boldsymbol{\Sigma}_{\xi, t-1} \mathbf{G}_{\xi}^{T}+\mathbf{G}_{u}^{\prime} \boldsymbol{\Sigma}_{u} \mathbf{G}^{\prime}{ }_{u}^{T}\tag{2} Σˉξ,t=GξΣξ,t−1GξT+Gu′ΣuG′uT(2)
原文对公式(2)称之为位姿在 t t t时刻的协方差,感觉不是很对,应该是 t t t 时刻 先验位姿误差的协方差?不是 Σ ξ , t \mathbf{\Sigma}_{\xi, t} Σξ,t 而是 Σ ˉ ξ , t \bar \mathbf{\Sigma}_{\xi, t} Σˉξ,t.
G ξ = ∂ ξ t ∂ ξ t − 1 = [ 1 0 − Δ s sin ( θ t − 1 + Δ θ / 2 ) 0 1 Δ s cos ( θ t − 1 + Δ θ / 2 ) 0 0 1 ] (3) \mathbf{G}_{\xi}=\frac{\partial \xi_{t}}{\partial \xi_{t-1}}=\left[\begin{array}{ccc} 1 & 0 & -\Delta s \sin (\theta_{t-1}+\Delta \theta / 2) \\ 0 & 1 & \Delta s \cos (\theta_{t-1}+\Delta \theta / 2) \\ 0 & 0 & 1 \end{array}\right]\tag{3} Gξ=∂ξt−1∂ξt=⎣⎡100010−Δssin(θt−1+Δθ/2)Δscos(θt−1+Δθ/2)1⎦⎤(3)
/* 构造 G_xi */
Eigen::Matrix3d G_xi;
G_xi << 1.0, 0.0, -delta_s * sin_tmp_th,
0.0, 1.0, delta_s * cos_tmp_th,
0.0, 0.0, 1.0;
控制输入为 u = [ Δ s r Δ s l ] T \mathbf{u}=\left[\begin{array}{ll} \Delta s_{r} & \Delta s_{l} \end{array}\right]^{T} u=[ΔsrΔsl]T
这里的求导有点耐人寻味,按理说应该是求 ∂ ξ t ∂ u t − 1 \frac{\partial \xi_{t}}{\partial \mathbf{u_{t-1}}} ∂ut−1∂ξt,但可以看出推导过程使用的是 ∂ ξ t ∂ u t \frac{\partial \xi_{t}}{\partial \mathbf{u_t}} ∂ut∂ξt:
G u ′ = ∂ ξ t ∂ u = [ 1 2 cos ( θ t − 1 + Δ θ 2 ) − Δ s 2 b sin ( θ t − 1 + Δ θ 2 ) 1 2 cos ( θ t − 1 + Δ θ 2 ) + Δ s 2 b sin ( θ t − 1 + Δ θ 2 ) 1 2 sin ( θ t − 1 + Δ θ 2 ) + Δ s 2 b cos ( θ t − 1 + Δ θ 2 ) 1 2 sin ( θ t − 1 + Δ θ 2 ) − Δ s 2 b cos ( θ t − 1 + Δ θ 2 ) 1 b − 1 b ] (4) \mathbf{G}_{u}^{\prime}=\frac{\partial \xi_{t}}{\partial \mathbf{u}}=\left[\begin{array}{cc} \frac{1}{2} \cos \left(\theta_{t-1}+\frac{\Delta \theta}{2}\right)-\frac{\Delta s}{2 b} \sin \left(\theta_{t-1}+\frac{\Delta \theta}{2}\right) & \frac{1}{2} \cos \left(\theta_{t-1}+\frac{\Delta \theta}{2}\right)+\frac{\Delta s}{2 b} \sin \left(\theta_{t-1}+\frac{\Delta \theta}{2}\right) \\ \frac{1}{2} \sin \left(\theta_{t-1}+\frac{\Delta \theta}{2}\right)+\frac{\Delta s}{2 b} \cos \left(\theta_{t-1}+\frac{\Delta \theta}{2}\right) & \frac{1}{2} \sin \left(\theta_{t-1}+\frac{\Delta \theta}{2}\right)-\frac{\Delta s}{2 b} \cos \left(\theta_{t-1}+\frac{\Delta \theta}{2}\right) \\ \frac{1}{b} & -\frac{1}{b} \end{array}\right]\tag{4} Gu′=∂u∂ξt=⎣⎡21cos(θt−1+2Δθ)−2bΔssin(θt−1+2Δθ)21sin(θt−1+2Δθ)+2bΔscos(θt−1+2Δθ)b121cos(θt−1+2Δθ)+2bΔssin(θt−1+2Δθ)21sin(θt−1+2Δθ)−2bΔscos(θt−1+2Δθ)−b1⎦⎤(4)
/* 构造 Gu' */
Eigen::Matrix<double, 3, 2> Gup;
Gup << 0.5 * (cos_tmp_th - delta_s * sin_tmp_th / b_), 0.5 * (cos_tmp_th + delta_s * sin_tmp_th / b_),
0.5 * (sin_tmp_th + delta_s * cos_tmp_th / b_), 0.5 *(sin_tmp_th - delta_s * cos_tmp_th / b_),
1.0/b_ , -1.0/b_;
1.2.运动更新
可以看出1.1小节中只是对机器人位姿 ξ \xi ξ 进行了求偏导, 而状态量 X \mathbf{X} X 还包含了路标点。扩展路标点之后,运动方程为:
[ x y θ m x , 1 m y , 1 ⋮ m x , N m y , N ] t ⏟ X t = [ x y θ m x , 1 m y , 1 ⋮ m x , N m y , N ] t − 1 ⏟ x l − 1 + [ 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 ⋮ ⋮ ⋮ 0 0 0 0 0 0 ] ⏟ F [ Δ s cos ( θ t − 1 + Δ θ / 2 ) Δ s sin ( θ t − 1 + Δ θ / 2 ) Δ θ ] ⏟ g ( X t − 1 , u t ) (5) \underbrace{\left[\begin{array}{c} x \\ y \\ \theta \\ m_{x, 1} \\ m_{y, 1} \\ \vdots \\ m_{x, N} \\ m_{y, N} \end{array}\right]_{t}}_{\mathbf{X}_{t}} =\underbrace{\underbrace{\left[\begin{array}{c} x \\ y \\ \theta \\ m_{x, 1} \\ m_{y, 1} \\ \vdots \\ m_{x, N} \\ m_{y, N} \end{array}\right]_{t-1}}_{\mathbf{x}_{l-1}}+\underbrace{\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \vdots & \vdots & \vdots \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]}_{\mathbf{F}} \left[\begin{array}{c} \Delta s \cos (\theta_{t-1}+\Delta \theta / 2) \\ \Delta s \sin (\theta_{t-1}+\Delta \theta / 2) \\ \Delta \theta \end{array}\right]}_{\mathbf{g\left(\mathbf{X}_{t-1}, \mathbf{u}_{t}\right)}} \tag{5} Xt ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡xyθmx,1my,1⋮mx,Nmy,N⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤t=g(Xt−1,ut) xl−1 ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡xyθmx,1my,1⋮mx,Nmy,N⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤t−1+F ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡10000⋮0001000⋮0000100⋮00⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎡Δscos(θt−1+Δθ/2)Δssin(θt−1+Δθ/2)Δθ⎦⎤(5)
接下来是求解(不太明白这里为什么是 u t \mathbf{u}_t ut,而不是 u t − 1 \mathbf{u}_{t-1} ut−1):
Σ ‾ t = G t Σ t − 1 G t T + G u Σ u G u T (6) \overline{\boldsymbol{\Sigma}}_{t}=\mathbf{G}_{t} \boldsymbol{\Sigma}_{t-1} \mathbf{G}_{t}^{T}+\mathbf{G}_{u} \boldsymbol{\Sigma}_{u} \mathbf{G}_{u}^{T}\tag{6} Σt=GtΣt−1GtT+GuΣuGuT(6)
G t = ∂ g ( X t − 1 , u t ) ∂ X t − 1 = [ G ξ 0 0 I ] (7) \mathbf{G}_{t}= \frac{\partial g(\mathbf{X}_{t-1},\mathbf{u}_t)}{\partial \mathbf{X}_{t-1}}=\left[\begin{array}{cc} \mathbf{G}_{\xi} & \mathbf{0} \\ \mathbf{0} & \mathbf{I} \end{array}\right]\tag{7} Gt=∂Xt−1∂g(Xt−1,ut)=[Gξ00I](7)
G u = ∂ g ( X t − 1 , u t ) ∂ u t = F G u ′ (8) \mathbf{G}_{u}= \frac{\partial g(\mathbf{X}_{t-1},\mathbf{u}_t)}{\partial \mathbf{u}_{t}}=\mathbf{F} \mathbf{G}_{u}^{\prime}\tag{8} Gu=∂ut∂g(Xt−1,ut)=FGu′(8)
Σ ‾ t = [ G ξ 0 0 I ] Σ t − 1 [ G ξ T 0 0 I ] + F G ′ u Σ u G ′ u T F T = [ G ξ Σ x x G ξ T G ξ Σ x m ( G ξ Σ x m ) T Σ m m ] + F G u ′ Σ u G ′ u T F T (9) \begin{aligned} \overline{\boldsymbol{\Sigma}}_{t} &=\left[\begin{array}{cc} \mathbf{G}_{\xi} & \mathbf{0} \\ \mathbf{0} & \mathbf{I} \end{array}\right] \mathbf{\Sigma}_{t-1}\left[\begin{array}{cc} \mathbf{G}_{\xi}^{T} & \mathbf{0} \\ \mathbf{0} & \mathbf{I} \end{array}\right]+\mathbf{F} \mathbf{G}^{\prime}{ }_{u} \boldsymbol{\Sigma}_{u} \mathbf{G}^{\prime}{ }_{u}^{T} \mathbf{F}^{T} \\ &=\left[\begin{array}{cc} \mathbf{G}_{\xi} \boldsymbol{\Sigma}_{x x} \mathbf{G}_{\xi}^{T} & \mathbf{G}_{\xi} \boldsymbol{\Sigma}_{x m} \\ \left(\mathbf{G}_{\xi} \boldsymbol{\Sigma}_{x m}\right)^{T} & \boldsymbol{\Sigma}_{m m} \end{array}\right]+\mathbf{F} \mathbf{G}_{u}^{\prime} \boldsymbol{\Sigma}_{u} \mathbf{G}^{\prime}{ }_{u}^{T} \mathbf{F}^{T} \end{aligned}\tag{9} Σt=[Gξ00I]Σt−1[GξT00I]+FG′uΣuG′uTFT=[GξΣxxGξT(GξΣxm)TGξΣxmΣmm]+FGu′ΣuG′uTFT(9)
可以看出,运动更新同时影响了机器人位姿的协方差,以及位姿与地图之间的协方差。
// 根据此时状态量的维数,构建F\Gt矩阵
int N = mu_.rows(); // N = 3
Eigen::MatrixXd F(N, 3); F.setZero();
F.block(0,0, 3, 3) = Eigen::Matrix3d::Identity();
Eigen::MatrixXd Gt = Eigen::MatrixXd::Identity(N, N);
Gt.block(0, 0, 3, 3) = G_xi;
在代码中, Σ u \mathbf{\Sigma}_u Σu 的计算如下所示:
double k_; // 里程计协方差参数
sigma_u << k_ * k_ * delta_sr * delta_sr, 0.0,
0.0, k_ * k_* delta_sl * delta_sl;
对于协方差,查了一下,网上相同的内容好多,不知道谁是原创,贴一个参考链接.从参考可知,变量 X X X 按列排列时有:
Σ = 1 m ∑ i = 1 m ( X i ) ⋅ ( X i ) T \Sigma=\frac{1}{m} \sum_{i=1}^{m}\left(X^{i}\right) \cdot\left(X^{i}\right)^{T} Σ=m1i=1∑m(Xi)⋅(Xi)T里程计协方差参数选取蛮重要。
因此,最后的先验估计误差协方差矩阵,即公式(9)为:
/* 更新协方差, 代码中显然是 sigma_{t-1} , 原文公式表示有点不准确*/
sigma_ = Gt * sigma_ *Gt.transpose() + F * Gup * sigma_u * Gup.transpose() * F.transpose();
我计算出来的公式(9)是这样的:
Σ ‾ t = [ G ξ 0 0 I ] Σ t − 1 [ G ξ T 0 0 I ] + F G ′ u Σ u G ′ u T F T = [ G ξ Σ t − 1 G ξ T 0 0 Σ t − 1 ] + F G u ′ Σ u G ′ u T F T (9) \begin{aligned} \overline{\boldsymbol{\Sigma}}_{t} &=\left[\begin{array}{cc} \mathbf{G}_{\xi} & \mathbf{0} \\ \mathbf{0} & \mathbf{I} \end{array}\right] \mathbf{\Sigma}_{t-1}\left[\begin{array}{cc} \mathbf{G}_{\xi}^{T} & \mathbf{0} \\ \mathbf{0} & \mathbf{I} \end{array}\right]+\mathbf{F} \mathbf{G}^{\prime}{ }_{u} \boldsymbol{\Sigma}_{u} \mathbf{G}^{\prime}{ }_{u}^{T} \mathbf{F}^{T} \\ &=\left[\begin{array}{cc} \mathbf{G}_{\xi} \boldsymbol{\Sigma}_{t-1} \mathbf{G}_{\xi}^{T} &0 \\ 0& \boldsymbol{\Sigma}_{t-1} \end{array}\right]+\mathbf{F} \mathbf{G}_{u}^{\prime} \boldsymbol{\Sigma}_{u} \mathbf{G}^{\prime}{ }_{u}^{T} \mathbf{F}^{T} \end{aligned}\tag{9} Σt=[Gξ00I]Σt−1[GξT00I]+FG′uΣuG′uTFT=[GξΣt−1GξT00Σt−1]+FGu′ΣuG′uTFT(9)
我不太明白,这里作者是怎么展开的,请求各位看官大佬帮我解答一下。公式(9)对应EKF公式(2)
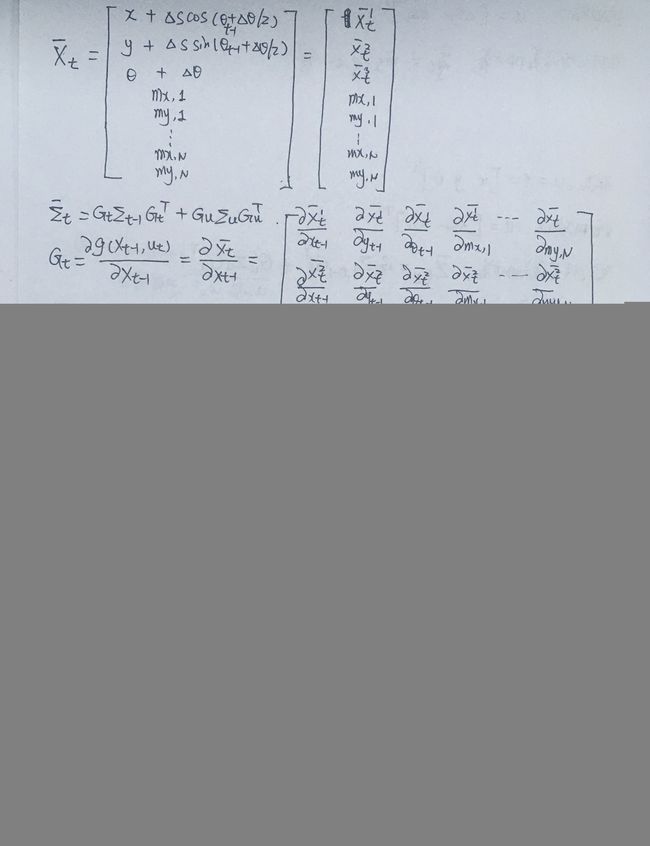
哦,傻逼了, Σ t − 1 \boldsymbol{\Sigma}_{t-1} Σt−1 要展开乘,但即便是展开乘,也应该是将 Σ t − 1 \boldsymbol{\Sigma}_{t-1} Σt−1展开,而不是 Σ t \boldsymbol{\Sigma}_{t} Σt
至此,EKF的前两个公式基本完成了。
2.测量模型
测量模型需要确定的量: 测量模型 h ( ∗ ) h(*) h(∗) 、 h ( ∗ ) h(*) h(∗) 对 X ~ t \tilde{X}_{t} X~t 的 Jacobian 矩阵 H t H_t Ht 、 h ( ∗ ) h(*) h(∗) 对测量噪声的 Jacobian 矩阵 V k V_k Vk、 测量噪声协方差矩阵 Q t Q_t Qt.
注意这里的 X ~ t = f ( X ^ t − 1 , u t − 1 , 0 ) \tilde{X}_{t}=f\left(\hat{X}_{t-1}, u_{t-1}, 0\right) X~t=f(X^t−1,ut−1,0), X ^ t − 1 \hat{X}_{t-1} X^t−1 为上一轮的后验估计。
首先解决测量值的问题。虽然可以获得ArUco码相对于机器人的6自由度位姿信息,但是为了与书上的观测统一,本文还是把相机作为Range-bearing传感器使用,也就是转换成距离 r r r 和角度 ϕ \phi ϕ 。1个ArUco码作为一个路标点 m m m,坐标为 [ m x m y ] T [m_x\ m_y]^T [mx my]T。
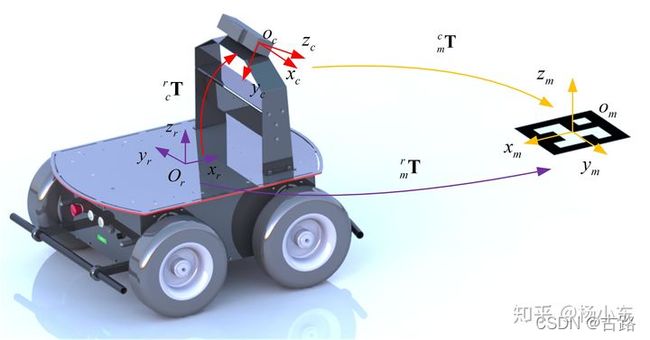
码与相机的相对位姿为 T c m \mathbf{T}_{cm} Tcm,相机与机器人的相对位姿为 T r c \mathbf{T}_{rc} Trc,那么码相对于机器人的位姿为 T r m = T r c T c m \mathbf{T}_{rm} = \mathbf{T}_{rc}\mathbf{T}_{cm} Trm=TrcTcm 。 T r m \mathbf{T}_{rm} Trm 的平移项 x x x 和 y y y 就是码的原点在机器人坐标系下的坐标。转化成距离信息就是 r = x 2 + y 2 r = \sqrt{x^2 + y^2} r=x2+y2,角度就是 ϕ = atan 2 ( y , x ) \phi=\operatorname{atan} 2(y, x) ϕ=atan2(y,x)。这样就得到了测量值 z = [ r ϕ ] T z=\left[\begin{array}{ll} r & \phi \end{array}\right]^{T} z=[rϕ]T。这里的箭头方向和自己的表达习惯依然是反的,注意不要混淆。
对于测量噪声协方差矩阵 Q \mathbf{Q} Q, 这里再做一个近似假设,认为观测的方差与距离和角度成线性关系:
Q = [ ∥ k r r ∥ 2 ∥ k ϕ ϕ ∥ 2 ] (10) \mathbf{Q}=\left[\begin{array}{cc} \left\|k_{r} r\right\|^{2} & \\ & \left\|k_{\phi} \phi\right\|^{2} \end{array}\right]\tag{10} Q=[∥krr∥2∥kϕϕ∥2](10)
这里的 k r k_r kr、 k ϕ k_{\phi} kϕ 怎么计算得来的?从代码中得到答案:初始化给定的。
/* 计算观测方差 */
Eigen::Matrix2d Q;
// 对应公式(10),这里的参数依据什么来设定? 测量为 z= [r, phi]
Q << k_r_ * k_r_* fabs(ob.r_ * ob.r_), 0.0,
0.0, k_phi_ * k_phi_ * fabs(ob.phi_ * ob.phi_);
第 i i i个路标点的观测模型为:
z t i = h ( X t ) + δ t i , δ t ∼ N ( 0 , Q t ) (11) \mathbf{z}_{t}^{i}=h\left(\mathbf{X}_{t}\right)+\delta_{t}^{i}, \delta_{t} \sim \mathcal{N}\left(\mathbf{0}, \mathbf{Q}_{t}\right)\tag{11} zti=h(Xt)+δti,δt∼N(0,Qt)(11)
展开来看:
{ r t i = ( m x , i − x ) 2 + ( m y , i − y ) 2 ϕ t i = atan 2 ( m y , i − y , m x , i − x ) − θ (12) \left\{\begin{array}{l} r_{t}^{i}=\sqrt{\left(m_{x, i}-x\right)^{2}+\left(m_{y, i}-y\right)^{2}} \\ \phi_{t}^{i}=\operatorname{atan} 2\left(m_{y, i}-y, m_{x, i}-x\right)-\theta \end{array}\right.\tag{12} {rti=(mx,i−x)2+(my,i−y)2ϕti=atan2(my,i−y,mx,i−x)−θ(12)
这里的相机测量有点类似于将其看做是二维激光的数据,方便计算吧,公式也简单。测量值最后是在robot坐标系下表示的,不是在相机坐标系,这个坐标系的变换过程其实就是 ( m x , i − x ) \left(m_{x, i}-x\right) (mx,i−x) 、 ( m y , i − y ) \left(m_{y, i}-y\right) (my,i−y)、 − θ -\theta −θ 的过程。
cv::Rodrigues(rvec, R);
Eigen::Matrix4d T_c_m;
// 旋转 + 平移: marker to camera , 也是 marker 在 camera 坐标系下的位姿
T_c_m << R.at<double>(0, 0), R.at<double>(0, 1), R.at<double>(0, 2), tvec[0],
R.at<double>(1, 0), R.at<double>(1, 1), R.at<double>(1, 2), tvec[1],
R.at<double>(2, 0), R.at<double>(2, 1), R.at<double>(2, 2), tvec[2],
0.,0.,0.,1.;
// marker to robot ,也是 marker 在 robot 坐标系下的位姿
Eigen::Matrix4d T_r_m = T_r_c_ * T_c_m; // T_r_c_ 外参
// 转为观测模型的测量值
double& x = T_r_m(0, 3);
double& y = T_r_m(1, 3);
double r = sqrt(x*x + y*y);
double phi = atan2(y, x);
int aruco_id = IDs[i];
程序逻辑上,接下来这部分计算应该是在地图点添加之后进行,因为初始化是状态量只有机器人位姿。
根据扩展卡尔曼滤波,需要求解观测 z t i \mathbf{z}_t^i zti 相对于 X ~ t \tilde{X}_{t} X~t (感觉原文表述不是很正确?)的雅克比 H t i \mathbf{H}_t^i Hti,实际上一个路标点观测只涉及到机器人的位姿和这个路标点的坐标,组合在一起就是五个量: v = [ x y θ m x , i m y , i ] v = [x\ y\ \theta\ m_{x,i}\ m_{y,i}] v=[x y θ mx,i my,i]。于是,观测 z t i \mathbf{z}_t^i zti 相对于 v v v 的雅克比是:
H ν = ∂ h ∂ ν = 1 q i [ − q i δ x i − q i δ y i 0 q i δ x i q i δ y i δ y i − δ x i − q i − δ y i δ x i ] ( { δ x i = m x , i − x δ y i = m y , i − y q i = δ x i 2 + δ y i 2 ) (13) \mathbf{H}_{\nu}=\frac{\partial h}{\partial \nu}=\frac{1}{q_i}\left[\begin{array}{ccccc} -\sqrt{q_i} \delta_{x_i} & -\sqrt{q_i} \delta_{y_i} & 0 & \sqrt{q_i} \delta_{x_i} & \sqrt{q_i} \delta_{y_i} \\ \delta_{y_i} & -\delta_{x_i} & -q_i & -\delta_{y_i} & \delta_{x_i} \end{array}\right]\left(\left\{\begin{array}{l} \delta_{x_i}=m_{x, i}-x \\ \delta_{y_i}=m_{y, i}-y \end{array} q_i=\delta_{x_i}^{2}+\delta_{y_i}^{2}\right)\right.\tag{13} Hν=∂ν∂h=qi1[−qiδxiδyi−qiδyi−δxi0−qiqiδxi−δyiqiδyiδxi]({δxi=mx,i−xδyi=my,i−yqi=δxi2+δyi2)(13)
最后提一个 1 / q 1/q 1/q 出去就是。
原文公式14,写的2*(3+2N)维,应该是一次测量,最后扩展起来应该是2N*(3+2N),这一点留着在看代码的时候求证吧。
// 公式14 F_i
int N = mu_.rows();
Eigen::MatrixXd F(5, N);
F.setZero();
F.block(0,0,3,3) = Eigen::Matrix3d::Identity();
F(3, 3 + 2*i) = 1;
F(4, 4 + 2*i) = 1;
// 公式13 中一些中间变量的计算
double& mx = mu_(3 + 2*i, 0);
double& my = mu_(4 + 2*i, 0);
double& x = mu_(0,0);
double& y = mu_(1,0);
double& theta = mu_(2,0);
double delta_x = mx - x;
double delta_y = my -y;
double q = delta_x * delta_x + delta_y * delta_y;
double sqrt_q = sqrt(q);
// 公式14
Eigen::MatrixXd Hv(2, 5);
Hv << -sqrt_q * delta_x, -sqrt_q* delta_y, 0, sqrt_q*delta_x, sqrt_q*delta_y,
delta_y, -delta_x, -q, -delta_y, delta_x;
Hv = (1/q) * Hv;
Eigen::MatrixXd Ht = Hv * F;
H ν \mathbf{H}_{\nu} Hν 维数 25, F i \mathbf{F}_i Fi 维数 5 (2N+3) ; H t i \mathbf{H}_t^i Hti维数则为 2*(2N+3),对于N个数据观测则是2N*(2N+3)维,不知道这样理解是否正确。看代码求证。
K t i = Σ ˉ t H t i T ( H t i Σ ˉ t H t i T + Q t ) − 1 μ t = μ ˉ t + K t i ( z t − h ( μ ˉ t ) ) Σ t = ( I − K t i H t i ) Σ ˉ t (15) \begin{aligned} &K_{t}^i=\bar{\Sigma}_{t} H_{t}^{iT}\left(H_{t} ^i\bar{\Sigma}_{t} H_{t}^{iT}+Q_{t}\right)^{-1} \\ &\mu_{t}=\bar{\mu}_{t}+K_{t}^i\left(z_{t}-h\left(\bar{\mu}_{t}\right)\right) \\ &\Sigma_{t}=\left(I-K_{t}^i H_{t}^i\right) \bar{\Sigma}_{t} \end{aligned}\tag{15} Kti=ΣˉtHtiT(HtiΣˉtHtiT+Qt)−1μt=μˉt+Kti(zt−h(μˉt))Σt=(I−KtiHti)Σˉt(15)
// 公式15 EKF的后三个公式
// kalman 增益
Eigen::MatrixXd K = sigma_ * Ht.transpose()*( Ht * sigma_ * Ht.transpose() + Q ).inverse();
double phi_hat = atan2(delta_y, delta_x)- theta;
normAngle(phi_hat);
Eigen::Vector2d z_hat(
sqrt_q, phi_hat
);
Eigen::Vector2d z(ob.r_, ob.phi_);
mu_ = mu_ + K * (z - z_hat);
Eigen::MatrixXd I = Eigen::MatrixXd::Identity(N, N);
sigma_ = ( I - K * Ht) * sigma_;
h ( μ ˉ t ) = z ^ t i = [ ( m ˉ x , i − x ˉ ) 2 + ( m ˉ y , i − y ˉ ) 2 atan 2 ( m ˉ y , i − y ˉ , m ˉ x , i − x ˉ ) − θ ˉ ] (16) h\left(\bar{\mu}_{t}\right) = \hat{\mathbf{z}}_{t}^{i}=\left[\begin{array}{l} \sqrt{\left(\bar{m}_{x, i}-\bar{x}\right)^{2}+\left(\bar{m}_{y, i}-\bar{y}\right)^{2}} \\ \operatorname{atan} 2\left(\bar{m}_{y, i}-\bar{y}, \bar{m}_{x, i}-\bar{x}\right)-\bar{\theta} \end{array}\right]\tag{16} h(μˉt)=z^ti=[(mˉx,i−xˉ)2+(mˉy,i−yˉ)2atan2(mˉy,i−yˉ,mˉx,i−xˉ)−θˉ](16)
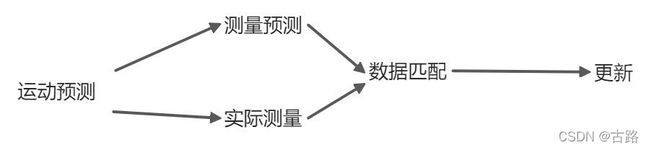
此图来自ref02.EKF_SLAM实践。至此,就完成了状态量的驱动与更新。
3.地图更新
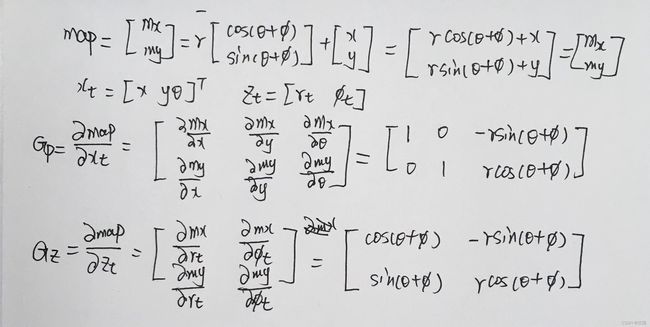
上文所说的操作都是假设路标点的数量是已知的,这个值也可以认为是不知道的,可以边运行边加入路标点:当看到一个新的地图点时就扩展状态空间和协方差。当观测到一个新的路标点,其观测为 z = [ r ϕ ] T z=\left[\begin{array}{ll} r & \phi \end{array}\right]^{T} z=[rϕ]T,此时的机器人位姿为 x t = ( x , y , θ ) T x_{t}=(x, y, \theta)^{T} xt=(x,y,θ)T 根据机器人的位姿可以计算地图点的坐标为:
m a p = [ m x m y ] = [ cos ( θ ) − sin ( θ ) sin ( θ ) cos ( θ ) ] [ r cos ( ϕ ) r sin ( ϕ ) ] + [ x y ] = r [ cos ( θ + ϕ ) sin ( θ + ϕ ) ] + [ x y ] (17) map = \left[\begin{array}{l} m_{x} \\ m_{y} \end{array}\right]=\left[\begin{array}{cc} \cos (\theta) & -\sin (\theta) \\ \sin (\theta) & \cos (\theta) \end{array}\right]\left[\begin{array}{c} r \cos (\phi) \\ r \sin (\phi) \end{array}\right]+\left[\begin{array}{l} x \\ y \end{array}\right]=r\left[\begin{array}{c} \cos (\theta+\phi) \\ \sin (\theta+\phi) \end{array}\right]+\left[\begin{array}{l} x \\ y \end{array}\right]\tag{17} map=[mxmy]=[cos(θ)sin(θ)−sin(θ)cos(θ)][rcos(ϕ)rsin(ϕ)]+[xy]=r[cos(θ+ϕ)sin(θ+ϕ)]+[xy](17)
// 添加新路标
/* 均值 */
double angle = mu_(2,0) + ob.phi_;
normAngle(angle);
double mx = ob.r_ * cos(angle) + mu_(0,0);
double my = ob.r_ * sin(angle) + mu_(1,0);
3.1.新地图点的协方差
这部分可以参考ref02.EKF_SLAM实践4.5小节-状态向量增广。
地图点的协方差为:
Σ m m = G p Σ ξ G p T + G z Q G z T (18) \mathbf{\Sigma}_{mm}=\mathbf{G}_{p} \mathbf{\Sigma}_{\xi} \mathbf{G}_{p}^{T}+\mathbf{G}_{z} \mathbf{Q} \mathbf{G}_{z}^{T}\tag{18} Σmm=GpΣξGpT+GzQGzT(18)
问:这里为什么要乘 Σ ξ \mathbf{\Sigma}_\xi Σξ?
G p = [ 1 0 − r sin ( θ + ϕ ) 0 1 r cos ( θ + ϕ ) ] (19) G_{p}=\left[\begin{array}{ccc} 1 & 0 & -r \sin (\theta+\phi) \\ 0 & 1 & r \cos (\theta+\phi) \end{array}\right]\tag{19} Gp=[1001−rsin(θ+ϕ)rcos(θ+ϕ)](19) G z = [ cos ( θ + ϕ ) − r sin ( θ + ϕ ) sin ( θ + ϕ ) r cos ( θ + ϕ ) ] (20) G_{z}=\left[\begin{array}{cc} \cos (\theta+\phi) & -r \sin (\theta+\phi) \\ \sin (\theta+\phi) & r \cos (\theta+\phi) \end{array}\right]\tag{20} Gz=[cos(θ+ϕ)sin(θ+ϕ)−rsin(θ+ϕ)rcos(θ+ϕ)](20)
Eigen::Matrix3d sigma_xi = sigma_.block(0,0, 3, 3);
Eigen::Matrix<double, 2, 3> Gp;
Gp << 1, 0, -ob.r_ * sin(angle),
0, 1, ob.r_ * cos(angle);
Eigen::Matrix2d Gz;
Gz << cos(angle), -ob.r_ * sin(angle),
sin(angle), ob.r_ * cos(angle);
// 新地图点的协方差
Eigen::Matrix2d sigma_m = Gp * sigma_xi * Gp.transpose() + Gz * Q * Gz.transpose();
3.2 新地图点与原状态之间的协方差
下面,还需要计算新加入的状态(地图点)与原状态(1个机器人位姿+N个地图点)之间的协方差。
Σ m x = G f x Σ t (21) \mathbf{\Sigma}_{m x}=\mathbf{G}_{f x} \mathbf{\Sigma}_{t}\tag{21} Σmx=GfxΣt(21)
问:为什么要乘以 Σ t \mathbf{\Sigma}_t Σt ?
Σ t \mathbf{\Sigma}_t Σt 为原状态的协方差矩阵, Σ f x \mathbf{\Sigma}_{fx} Σfx 为(17)式相对于原状态的雅克比矩阵:
G f x = [ 1 0 − r sin ( θ + ϕ ) 0 ⋯ 0 0 1 r cos ( θ + ϕ ) 0 ⋯ 0 ] (22) \mathbf{G}_{f x}=\left[\begin{array}{cccccc} 1 & 0 & -r \sin (\theta+\phi) & 0 & \cdots & 0 \\ 0 & 1 & r \cos (\theta+\phi) & 0 & \cdots & 0 \end{array}\right]\tag{22} Gfx=[1001−rsin(θ+ϕ)rcos(θ+ϕ)00⋯⋯00](22)
// 新地图点相对于已有状态的协方差, Gfx的维数为当前状态量的维数
Eigen::MatrixXd Gfx;
Gfx.resize ( 2, mu_.rows() );
Gfx.setZero();
Gfx.block ( 0,0, 2, 3 ) = Gp;
此时就可以得出公式21:
Eigen::MatrixXd sigma_mx;
sigma_mx.resize ( 2, mu_.rows() );
sigma_mx.setZero();
sigma_mx = Gfx * sigma_;
/**** 加入到地图中: 矩阵增广 ****/
/* 扩展均值 = 状态量 */
int N = mu_.rows();
// 一次观测只有 一个地图点,mx, my 所以是 N(原来的)+2(新地图点)
Eigen::MatrixXd tmp_mu ( N + 2, 1 );
tmp_mu.setZero();
tmp_mu << mu_ , mx, my;
mu_.resize ( N+2, 1 );
mu_ = tmp_mu;
/* 扩展协方差 : 按照图示矩阵进行拼接,同样的,一次加一个观测进去*/
Eigen::MatrixXd tmp_sigma ( N+2, N+2 );
tmp_sigma.setZero();
tmp_sigma.block ( 0, 0, N, N ) = sigma_;
tmp_sigma.block ( N, N, 2, 2 ) = sigma_m;
tmp_sigma.block ( N, 0, 2, N ) = sigma_mx;
tmp_sigma.block ( 0, N, N, 2 ) = sigma_mx.transpose();
sigma_.resize ( N+2, N+2 );
sigma_ = tmp_sigma;
这部分代码,可以引入内存管理,不然每次都copy有点费时间。至此,EKF算法中所有的模型都已建立完毕。
4.数据关联
从参考材料ref01\ref02可知,完整的流程为:
- 运动预测
- 测量预测
- 测量
- 数据关联
- 更新
还有很重要的一步,数据关联。这个系统中marker有唯一的ID,所以省去了很多工作,可以节约时间,只关注EKF部分的学习,感谢原博主的开源。
显示的过程,知乎上也有评论指出,成员变量一边读一边写,可能容易出问题; 另外,矩阵好像只有增广,没有margin,如果marker一直增加的话,可能就爆炸了。不过作为学习材料十分牛逼了,感谢原博主的开源。
5.demo
- aruco竟然是在opencv_contrib里面。
- aruco参考。
- 最近没咋用opencv_contrib,再装一遍吧,Ubuntu18.04安装OpenCV3.4.15+opencv_contrib
还在下载数据集…,demo待测试。
更。
这个aruco按照原博主的参数,在我这儿无法检测,也尝试了好几个版本,应该是参数有问题,调了好久,不好调,得需要知道dictionary参数,原博主给的dictionary参数在我这儿又无法检测。心碎,最后把OpenCV-contribute模块中的aruco扣出来,挨着debug,也没办法得到很好的检测效果。心伤了。
有调出来的朋友,留言告知一下参数或者是其他什么错误,谢谢了。