SSD(Single Shot MultiBox Detector)

一.概述

                 

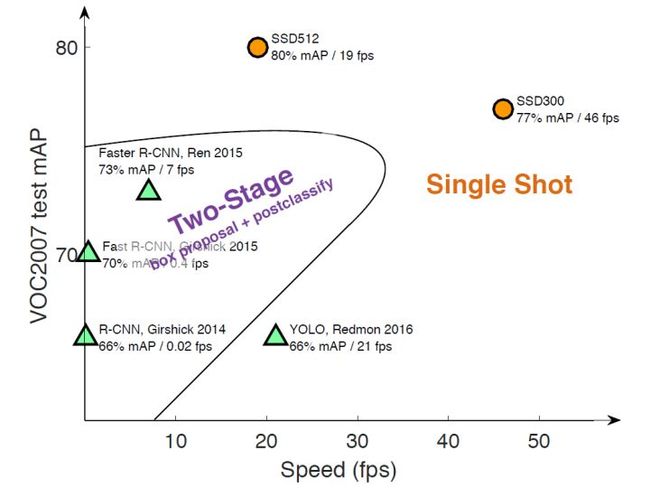
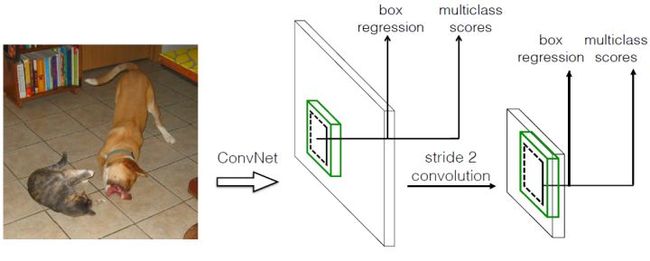
本文讲解的是SSD算法，其英文全名是Single Shot MultiBox Detector，名字取得不错，Single shot指明了SSD算法属于one-stage方法，MultiBox指明了SSD是多框预测。从图1可以看到，SSD算法在准确度和速度（除了SSD512）上都比Yolo要好很多。图2给出了不同算法的基本框架图，对于Faster R-CNN，其先通过CNN得到候选框，然后再进行分类与回归，而Yolo与SSD可以一步到位完成检测。相比Yolo，SSD采用CNN来直接进行检测，而不是像Yolo那样在全连接层之后做检测。其实采用卷积直接做检测只是SSD相比Yolo的其中一个不同点，另外还有两个重要的改变，一是SSD提取了不同尺度的特征图来做检测，大尺度特征图（较靠前的特征图）可以用来检测小物体，而小尺度特征图（较靠后的特征图）用来检测大物体；二是SSD采用了不同尺度和长宽比的先验框（Prior boxes, Default boxes，在Faster R-CNN中叫做锚，Anchors）。Yolo算法缺点是难以检测小目标，而且定位不准，但是这几点重要改进使得SSD在一定程度上克服这些缺点。下面我们详细讲解SDD算法的原理。

                      

这篇文章在既保证速度，又要保证精度的情况下，提出了 SSD 物体检测模型，与现在流行的检测模型一样，将检测过程整个成一个 single deep neural network。便于训练与优化，同时提高检测速度。

SSD 将输出一系列 离散化（discretization） 的 bounding boxes，这些 bounding boxes 是在 不同层次（layers） 上的 feature maps 上生成的，并且有着不同的 aspect ratio。

在 prediction 阶段：

要计算出每一个 default box 中的物体，其属于每个类别的可能性，即 score，得分。如对于 PASCAL VOC 数据集，总共有 20 类，那么得出每一个 bounding box 中物体属于这 20 个类别的每一种的可能性。

同时，要对这些 bounding boxes 的 shape 进行微调，以使得其符合物体的 外接矩形。

还有就是，为了处理相同物体的不同尺寸的情况，SSD 结合了不同分辨率的 feature maps 的 predictions。

相对于那些需要 object proposals 的检测模型，本文的 SSD 方法完全取消了 proposals generation、pixel resampling 或者 feature resampling 这些阶段。这样使得 SSD 更容易去优化训练，也更容易地将检测模型融合进系统之中。

在 PASCAL VOC、MS COCO、ILSVRC 数据集上的实验显示，SSD 在保证精度的同时，其速度要比用 region proposals 的方法要快很多。

SSD 相比较于其他单结构模型（YOLO），SSD 取得更高的精度，即是是在输入图像较小的情况下。如输入 300×300300×300 大小的 PASCAL VOC 2007 test 图像，在 Titan X 上，SSD 以 58 帧的速率，同时取得了 72.1% 的 mAP。

如果输入的图像是 500×500500×500，SSD 则取得了 75.1% 的 mAP，比目前最 state-of-art 的 Faster R-CNN 要好很多。
 

二.设计理念

SSD和Yolo一样都是采用一个CNN网络来进行检测，但是却采用了多尺度的特征图，其基本架构如下图所示。下面将SSD核心设计理念总结为以下三点：

           

（1）采用多尺度特征图用于检测

截断basenetwork，即去掉其最后的fc层，引入卷积层做最后的预测。所谓多尺度采用大小不同的特征图，CNN网络一般前面的特征图比较大，后面会逐渐采用stride=2的卷积或者pool来降低特征图大小，这正如图3所示，一个比较大的特征图和一个比较小的特征图，它们都用来做检测。这样做的好处是比较大的特征图来用来检测相对较小的目标，而小的特征图负责检测大目标，如图4所示，8x8的特征图可以划分更多的单元，但是其每个单元的先验框尺度比较小。（总共用6个特征图进行检测）

                               

（2）采用卷积进行检测

与Yolo最后采用全连接层不同，SSD直接采用卷积对不同的特征图来进行提取检测结果。对于形状为的特征图，只需要采用这样比较小的卷积核得到检测值。

3）设置先验框

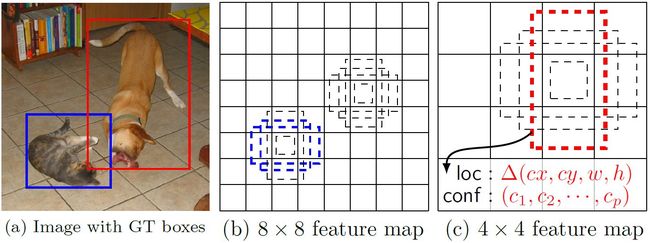
在Yolo中，每个单元预测多个边界框，但是其都是相对这个单元本身（正方块），但是真实目标的形状是多变的，Yolo需要在训练过程中自适应目标的形状。而SSD借鉴了Faster R-CNN中anchor的理念，每个单元设置尺度或者长宽比不同的先验框，预测的边界框（bounding boxes）是以这些先验框为基准的，在一定程度上减少训练难度。一般情况下，每个单元会设置多个先验框，其尺度和长宽比存在差异，如下图所示，可以看到每个单元使用了4个不同的先验框，图片中猫和狗分别采用最适合它们形状的先验框来进行训练，后面会详细讲解训练过程中的先验框匹配原则。

对于featuremap上的每个cell，对应k个bounding box，每一个bounding box预测c个类别分数和4个相对于先验anchor的offset，

这样每一个cell对应个filter，这些filter一般都是3*3大小的，即为featuremap为m*n*p，则filter对应为3*3*p*(k*(c+4))的维度尺寸，在卷积时通过padding使得卷积后的featuremap与用作卷积的featuremap大小相同，即都是m*n。

                    

该副图的说明如下：

SSD的检测值也与Yolo不太一样。对于每个单元的每个先验框，其都输出一套独立的检测值，对应一个边界框，主要分为两个部分。第一部分是各个类别的置信度或者评分，值得注意的是SSD将背景也当做了一个特殊的类别，如果检测目标共有c个类别，SSD其实需要预测c+1个置信度值，其中第一个置信度指的是不含目标或者属于背景的评分。后面当我们说c个类别置信度时，请记住里面包含背景那个特殊的类别，即真实的检测类别只有c-1个。在预测过程中，置信度最高的那个类别就是边界框所属的类别，特别地，当第一个置信度值最高时，表示边界框中并不包含目标。第二部分就是边界框的location，包含4个值，分别表示边界框的中心坐标以及宽高。但是真实预测值其实只是边界框相对于先验框的转换值(paper里面说是offset，但是觉得transformation更合适，参见R-CNN)。先验框位置用表示，其对应边界框用表示，那么边界框的预测值 l 其实是 b 相对于 d 的转换值：

                                                          

                                                          

习惯上，我们称上面这个过程为边界框的编码（encode），预测时，你需要反向这个过程，即进行解码（decode），从预测值 l中得到边界框的真实位置b：

                                                               

然而，在SSD的Caffe源码实现中还有trick，那就是设置variance超参数来调整检测值，通过bool参数variance_encoded_in_target来控制两种模式，当其为True时，表示variance被包含在预测值中，就是上面那种情况。但是如果是False（大部分采用这种方式，训练更容易？），就需要手动设置超参数variance，用来对 l 的4个值进行放缩，此时边界框需要这样解码：

                                             

综上所述，对于一个大小的特征图，共有个单元，每个单元设置的先验框数目记为k，那么每个单元共需要个预测值，所有的单元共需要个预测值，由于SSD采用卷积做检测，所以就需要个卷积核完成这个特征图的检测过程。

三.网络结构

SSD采用VGG16作为基础模型，然后在VGG16的基础上新增了卷积层来获得更多的特征图以用于检测。SSD的网络结构如下图所示。上面是SSD模型，下面是Yolo模型，可以明显看到SSD利用了多尺度的特征图做检测。模型的输入图片大小是 （还可以是，其与前者网络结构没有差别，只是最后新增一个卷积层，本文不再讨论）。                      

采用VGG16做基础模型，首先VGG16是在ILSVRC CLS-LOC数据集预训练。然后借鉴了DeepLab-LargeFOV，分别将VGG16的全连接层fc6和fc7转换成卷积层 conv6和 卷积层conv7，同时将池化层pool5由原来的stride=2的变成stride=1的 （猜想是不想reduce特征图大小），为了配合这种变化，采用了一种Atrous Algorithm，其实就是conv6采用扩展卷积或带孔卷积（Dilation Conv），其在不增加参数与模型复杂度的条件下指数级扩大卷积的视野，其使用扩张率(dilation rate)参数，来表示扩张的大小，如下图所示，(a)是普通的卷积，其视野就是 ，(b)是扩张率为2，此时视野变成，(c)扩张率为4时，视野扩大为 ，但是视野的特征更稀疏了。Conv6采用大小但dilation rate=6的扩展卷积。

                    

然后移除dropout层和fc8层，并新增一系列卷积层，在检测数据集上做finetuing。

其中VGG16中的Conv4_3层将作为用于检测的第一个特征图。conv4_3层特征图大小是，但是该层比较靠前，其norm较大，所以在其后面增加了一个L2 Normalization层（参见ParseNet），以保证和后面的检测层差异不是很大，这个和Batch Normalization层不太一样，其仅仅是对每个像素点在channle维度做归一化，而Batch Normalization层是在[batch_size, width, height]三个维度上做归一化。归一化后一般设置一个可训练的放缩变量gamma，使用TF可以这样简单实现：

# l2norm (not bacth norm, spatial normalization)
def l2norm(x, scale, trainable=True, scope="L2Normalization"):
    n_channels = x.get_shape().as_list()[-1]
    l2_norm = tf.nn.l2_normalize(x, [3], epsilon=1e-12)
    with tf.variable_scope(scope):
        gamma = tf.get_variable("gamma", shape=[n_channels, ], dtype=tf.float32,
                                initializer=tf.constant_initializer(scale),
                                trainable=trainable)
        return l2_norm * gamma

从后面新增的卷积层中提取Conv7，Conv8_2，Conv9_2，Conv10_2，Conv11_2作为检测所用的特征图，加上Conv4_3层，共提取了6个特征图，其大小分别是，但是不同特征图设置的先验框数目不同（同一个特征图上每个单元设置的先验框是相同的，这里的数目指的是一个单元的先验框数目）。先验框的设置，包括尺度（或者说大小）和长宽比两个方面。对于先验框的尺度，其遵守一个线性递增规则：随着特征图大小降低，先验框尺度线性增加：

                                                       

其中m指的特征图个数，但却是5，因为第一层（Conv4_3层）是单独设置的，表示先验框大小相对于图片的比例，而和表示比例的最小值与最大值，paper里面取0.2和0.9。对于第一个特征图，其先验框的尺度比例一般设置为，那么尺度为。对于后面的特征图，先验框尺度按照上面公式线性增加，但是先将尺度比例先扩大100倍，此时增长步长为 ，这样各个特征图的为 ，将这些比例除以100，然后再乘以图片大小，可以得到各个特征图的尺度为，这种计算方式是参考SSD的Caffe源码。综上，可以得到各个特征图的先验框尺度。对于长宽比，一般选取，对于特定的长宽比，按如下公式计算先验框的宽度与高度（后面的均指的是先验框实际尺度，而不是尺度比例）：

                                                                             

默认情况下，每个特征图会有一个且尺度为的先验框，除此之外，还会设置一个尺度为且的先验框，这样每个特征图都设置了两个长宽比为1但大小不同的正方形先验框。注意最后一个特征图需要参考一个虚拟来计算 。因此，每个特征图一共有6个先验框，但是在实现时，Conv4_3，Conv10_2和Conv11_2层仅使用4个先验框，它们不使用长宽比为 的先验框。每个单元的先验框的中心点分布在各个单元的中心，即，其中为特征图的大小。

得到了特征图之后，需要对特征图进行卷积得到检测结果，下图给出了一个大小的特征图的检测过程。其中Priorbox是得到先验框，前面已经介绍了生成规则。检测值包含两个部分：类别置信度和边界框位置，各采用一次卷积来进行完成。令 为该特征图所采用的先验框数目，那么类别置信度需要的卷积核数量为，而边界框位置需要的卷积核数量为。由于每个先验框都会预测一个边界框，所以SSD300一共可以预测                                                                                                                                

个边界框，这是一个相当庞大的数字，所以说SSD本质上是密集采样。

                    

对于以上的default box的生成，如果还有疑惑，可见下面的源码：

class PriorBox(object):
    """Compute priorbox coordinates in center-offset form for each source
    feature map.
    """
    def __init__(self, cfg):
        super(PriorBox, self).__init__()
        self.image_size = cfg['min_dim'] # 图片尺寸：300
        # number of priors for feature map location (either 4 or 6)
        self.num_priors = len(cfg['aspect_ratios']) # featuremap上每一个点的prior box数量，为4或者6
        self.variance = cfg['variance'] or [0.1] # variance参数
        self.feature_maps = cfg['feature_maps'] # 做检测用的选取的featuremap的尺寸
        self.min_sizes = cfg['min_sizes'] 
        self.max_sizes = cfg['max_sizes']
        self.steps = cfg['steps'] # 放缩的尺寸，有关系：self.image_size/self.steps=self.feature_maps
        self.aspect_ratios = cfg['aspect_ratios'] # 纵横比
        self.clip = cfg['clip'] # 是否做clip操作
        self.version = cfg['name'] # coco or voc
        for v in self.variance:
            if v <= 0:
                raise ValueError('Variances must be greater than 0')

    def forward(self):
        mean = []
        for k, f in enumerate(self.feature_maps):
            for i, j in product(range(f), repeat=2):
                f_k = self.image_size / self.steps[k]
                # unit center x,y
                cx = (j + 0.5) / f_k
                cy = (i + 0.5) / f_k

                # aspect_ratio: 1
                # rel size: min_size
                s_k = self.min_sizes[k]/self.image_size
                mean += [cx, cy, s_k, s_k]

                # aspect_ratio: 1
                # rel size: sqrt(s_k * s_(k+1))
                s_k_prime = sqrt(s_k * (self.max_sizes[k]/self.image_size))
                mean += [cx, cy, s_k_prime, s_k_prime]

                # rest of aspect ratios
                for ar in self.aspect_ratios[k]:
                    mean += [cx, cy, s_k*sqrt(ar), s_k/sqrt(ar)]
                    mean += [cx, cy, s_k/sqrt(ar), s_k*sqrt(ar)]
        # back to torch land
        output = torch.Tensor(mean).view(-1, 4)
        if self.clip:
            output.clamp_(max=1, min=0)
        return output

四.训练过程

(1).先验框匹配

在训练过程中，首先要确定训练图片中的ground truth（真实目标）与哪个先验框来进行匹配，与之匹配的先验框所对应的边界框将负责预测它。在Yolo中，ground truth的中心落在哪个单元格，该单元格中与其IOU最大的边界框负责预测它。但是在SSD中却完全不一样，SSD的先验框与ground truth的匹配原则主要有两点。首先，对于图片中每个ground truth，找到与其IOU最大的先验框，该先验框与其匹配，这样，可以保证每个ground truth一定与某个先验框匹配。通常称与ground truth匹配的先验框为正样本（其实应该是先验框对应的预测box，不过由于是一一对应的就这样称呼了），反之，若一个先验框没有与任何ground truth进行匹配，那么该先验框只能与背景匹配，就是负样本。一个图片中ground truth是非常少的， 而先验框却很多，如果仅按第一个原则匹配，很多先验框会是负样本，正负样本极其不平衡，所以需要第二个原则。第二个原则是：对于剩余的未匹配先验框，若某个ground truth的IOU大于某个阈值（一般是0.5），那么该先验框也与这个ground truth进行匹配。这意味着某个ground truth可能与多个先验框匹配，这是可以的。但是反过来却不可以，因为一个先验框只能匹配一个ground truth，如果多个ground truth与某个先验框 IOU大于阈值，那么先验框只与IOU最大的那个先验框进行匹配。第二个原则一定在第一个原则之后进行，仔细考虑一下这种情况，如果某个ground truth所对应最大IOU小于阈值，并且所匹配的先验框却与另外一个ground truth的 IOU大于阈值，那么该先验框应该匹配谁，答案应该是前者，首先要确保某个ground truth一定有一个先验框与之匹配。但是，这种情况我觉得基本上是不存在的。由于先验框很多，某个ground truth的最大 IOU肯定大于阈值，所以可能只实施第二个原则既可以了，这里的就是只实施了第二个原则，但是这里的Pytorch两个原则都实施了。下图为一个匹配示意图，其中绿色的GT是ground truth，红色为先验框，FP表示负样本，TP表示正样本。

以上的匹配原则总结为：

1. 每一个gt与其IOU最大的先验框匹配
2. 在剩余的未匹配先验框，选择与gt的IOU超过阈值(默认为0.5)的先验框进行匹配
3. 整体原则：每一个gt必须至少有一个先验框匹配，一个gt可以同时匹配多个先验框，而一个先验框最多只能与一个gt进行匹配。

                                                 

尽管一个ground truth可以与多个先验框匹配，但是ground truth相对先验框还是太少了，所以负样本相对正样本会很多。为了保证正负样本尽量平衡，SSD采用了hard negative mining，就是对负样本进行抽样，抽样时按照置信度误差（预测背景的置信度越小，误差越大）进行降序排列，选取误差较大的top-k作为训练的负样本，以保证正负样本比例接近1:3。(这使得模型的收敛速度加快，整体的训练速度也更快)

hard negative mining:

negative，即负样本，hard 说明是难以正确分类的样本，也就是说在对负样本分类时候，loss比较大(label与prediction相差较大)的那些样本，也可以说是容易将负样本看成正样本的那些样本;

在SSD中，即将负样本按照背景的置信度进行升序排列，(背景置信度小即说明容易被分成目标的可能性大，即为hard negative样本)，选择top-k作为训练用的负样本，保证训练时正负样本比例接近1:3。

（2）损失函数

训练样本确定了，然后就是损失函数了。损失函数定义为位置误差（locatization loss， loc）与置信度误差（confidence loss, conf）的加权和：

                                                     

其中N是先验框的正样本数量。这里为一个指示参数，当 时表示第 i 个先验框与第 j 个ground truth匹配，并且ground truth的类别为 p 。c为类别置信度预测值。l 为先验框的所对应边界框的位置预测值，而 g 是ground truth的位置参数。对于位置误差，其采用Smooth L1 loss，定义如下：

                                                

由于 的存在，所以位置误差仅针对正样本进行计算。值得注意的是，要先对ground truth的 g 进行编码得到 ，因为预测值 l 也是编码值，若设置variance_encoded_in_target=True，编码时要加上variance：

                                            

对于置信度误差，其采用softmax loss:

                                      

权重系数 通过交叉验证设置为1。前一半是针对正样本的loss计算，后一半是针对负样本的loss计算。

（3）数据扩增

•  Use the entire original input image
• Sample a patch so that the minimum jaccard overlap with the objects is 0.1, 0.3, 0.5, 0.7, or 0.9. 
•  Randomly sample a patch. 

抽样得到的patch大小约占原图大小的[0.1，1]，这些patch的纵横比为0.5和2。如果gt的中心位于抽样的patch中间，则我们将该gt完整的保留。

对于原图和抽样得到的patch，以p=0.5的概率进行水平翻转，并施加光度变换进行数据增强。

总结如下：

采用数据扩增（Data Augmentation）可以提升SSD的性能，主要采用的技术有水平翻转（horizontal flip），随机裁剪加颜色扭曲（random crop & color distortion），随机采集块域（Randomly sample a patch）（获取小目标训练样本），如下图所示：

                     

                    

五.预测过程

预测过程比较简单，对于每个预测框，首先根据类别置信度确定其类别（置信度最大者）与置信度值，并过滤掉属于背景的预测框。然后根据置信度阈值（如0.5）过滤掉阈值较低的预测框。对于留下的预测框进行解码，根据先验框得到其真实的位置参数（解码后一般还需要做clip，防止预测框位置超出图片）。解码之后，一般需要根据置信度进行降序排列，然后仅保留top-k（如400）个预测框。最后就是进行NMS算法，过滤掉那些重叠度较大的预测框。最后剩余的预测框就是检测结果了。

总结如下：

1. 对于每一个预测框根据类别置信度值确定其预测的类别与置信度
2. 过滤掉属于背景的预测框
3. 过滤掉置信度值小于一定阈值的预测框(如<0.5)
4. 根据先验框得到剩余预测框真实的位置参数bx,by,bw,bh(做clip防止预测框位置超出图片)
5. 根据置信度进行降序排序，得到top-k个预测框，如400个
6. 对每一个类别分别进行nms，剩余的预测框即为预测结果。

六.模型分析

1.Data augmentation is crucial

2.More default box shapes is better.

3.Atrous is faster

4.Multiple output layers at different resolutions is better