使用穷举法求解权重图最大割问题
使用穷举法求解权重图最大割问题
在本文中,我们将介绍如何通过穷举法来计算权重图的最大割问题。权重图的构造大致为:
g = nx.Graph() # 先创建一个空图
# 添加边及其对应的权重
g.add_edge(0, 1, weight=0.1)
g.add_edge(1, 2, weight=0.2)
g.add_edge(2, 3, weight=0.3)
g.add_edge(3, 0, weight=0.1)
# g.add_weighted_edges_from([(0, 1, 0.1), (1, 2, 0.2), (2, 3, 0.3), (3, 0, 0.1)])
nx.draw(g, with_labels=True, font_weight='bold')
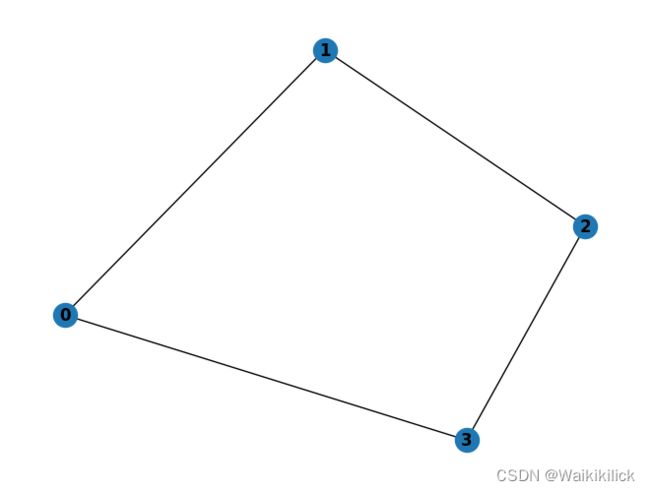
我们的目的是将图中四个顶点 0,1, 2, 3分为两组,使得连接两个组的所有边的权重和最大。
比如在此图中,如果我们将 0 和 2 划为一组,而 1 和 3 划为另一组,可以得到组间边为 01, 12, 23 和 30。权重和为 0.1 + 0.2 + 0.3 + 0.1 = 0.7 0.1+0.2+0.3+0.1=0.7 0.1+0.2+0.3+0.1=0.7。但如果我们将 0 划为一组,而 1, 2 和 3 划为另一组,可以得到组间边为 01 和 30。权重和为 0.1 + 0.1 = 0.2 0.1+0.1=0.2 0.1+0.1=0.2。
最大割问题就是讨论如何将顶点划分,所得到的割数,也就是组间权重和最大。
我们将整个求解过程分步进行分析。
最核心的部分是,如何将一个图以指定方式分为两组,并得到割数。我们以一个三顶点的图为例:
edges = {'12':0.5, '23':1} # 图的结构,两条边分别连接了 1 2 和 2 3 顶点,权重为 0.5 和 1
nodes = {1, 2, 3} # 图中所涉及到的顶点
nodes_left = {2} # 将顶点 2 放置于割图的一边,构成一个组
nodes_right = nodes - nodes_left # 其余顶点放置于割图的另一边,构成另一个组
cut = 0 # 割数 初始化为 0
# 将割边权重累加求和
for edge in edges.keys(): # 遍历所有的边
node_0 = int(edge[0]) # 边的两个顶点
node_1 = int(edge[1])
# 鉴别该边是否为割边:边的两个顶点是否分别在两个组里
if (node_0 in nodes_left and node_1 in nodes_right) or (node_0 in nodes_right and node_1 in nodes_left):
cut += edges[edge] # 如果为割边,就累加该权重
print(cut) # 打印割边权重和
1.5
对于一个稍复杂的图,比如四个顶点,存在顶点两两成组的情况。我们采用嵌套 for 循环来进行遍历。
edges = {'01':0.1, '12':0.2, '23':0.3, '03':0.4} # 定义构成图的边及其所对应的权重,每个边由其连接的两个顶点构成
nodes = {0, 1, 2, 3}
for i in list(nodes):
nodes_left = {i}
nodes_right = nodes - nodes_left
cut = 0
cut_edges = [] # 所有的割边
for edge in edges.keys():
node_0 = int(edge[0])
node_1 = int(edge[1])
if (node_0 in nodes_left and node_1 in nodes_right) or (node_0 in nodes_right and node_1 in nodes_left):
cut += edges[edge]
cut_edges.append(edge)
print('one size:', [i], '\tcut =', "%.1f" % cut, ' \tcut_edges are', cut_edges)
for j in range(i):
nodes_left = {i, j}
nodes_right = nodes - nodes_left
cut = 0
cut_edges = []
for edge in edges.keys():
node_0 = int(edge[0])
node_1 = int(edge[1])
if (node_0 in nodes_left and node_1 in nodes_right) or (node_0 in nodes_right and node_1 in nodes_left):
cut += edges[edge]
cut_edges.append(edge)
print('two size:', [i, j], 'cut =', "%.1f" % cut, ' \tcut_edges are', cut_edges)
one size: [0] cut = 0.5 cut_edges are ['01', '03']
one size: [1] cut = 0.3 cut_edges are ['01', '12']
two size: [1, 0] cut = 0.6 cut_edges are ['12', '03']
one size: [2] cut = 0.5 cut_edges are ['12', '23']
two size: [2, 0] cut = 1.0 cut_edges are ['01', '12', '23', '03']
two size: [2, 1] cut = 0.4 cut_edges are ['01', '23']
one size: [3] cut = 0.7 cut_edges are ['23', '03']
two size: [3, 0] cut = 0.4 cut_edges are ['01', '23']
two size: [3, 1] cut = 1.0 cut_edges are ['01', '12', '23', '03']
two size: [3, 2] cut = 0.6 cut_edges are ['12', '03']
为了便于使用,我们也可以进一步,根据边信息来自动确认所涉及的顶点。就得到了我们最终的求解程序。
edges = {'01':0.1, '12':0.2, '23':0.3, '30':-0.4}
nodes = set(int(i[0]) for i in edges.keys()) | set(int(i[1]) for i in edges.keys()) # 节点集为边中出现的所有顶点, | 操作为求并集
nodes_list = list(nodes)
for i in nodes_list:
nodes_left = {i}
nodes_right = nodes - nodes_left
cut = 0
cut_edges = []
for edge in edges.keys():
node_0 = int(edge[0])
node_1 = int(edge[1])
if (node_0 in nodes_left and node_1 in nodes_right) or (node_0 in nodes_right and node_1 in nodes_left):
cut += edges[edge]
cut_edges.append(edge)
print('one size:', [i], '\tcut =', "%.1f" % cut, ' \tcut_edges are', cut_edges)
for j in nodes_list[:nodes_list.index(i)]:
nodes_left = {i, j}
nodes_right = nodes - nodes_left
cut = 0
cut_edges = []
for edge in edges.keys():
node_0 = int(edge[0])
node_1 = int(edge[1])
if (node_0 in nodes_left and node_1 in nodes_right) or (node_0 in nodes_right and node_1 in nodes_left):
cut += edges[edge]
cut_edges.append(edge)
print('two size:', [i, j], 'cut =', "%.1f" % cut, ' \tcut_edges are', cut_edges)
one size: [0] cut = -0.3 cut_edges are ['01', '30']
one size: [1] cut = 0.3 cut_edges are ['01', '12']
two size: [1, 0] cut = -0.2 cut_edges are ['12', '30']
one size: [2] cut = 0.5 cut_edges are ['12', '23']
two size: [2, 0] cut = 0.2 cut_edges are ['01', '12', '23', '30']
two size: [2, 1] cut = 0.4 cut_edges are ['01', '23']
one size: [3] cut = -0.1 cut_edges are ['23', '30']
two size: [3, 0] cut = 0.4 cut_edges are ['01', '23']
two size: [3, 1] cut = 0.2 cut_edges are ['01', '12', '23', '30']
two size: [3, 2] cut = -0.2 cut_edges are ['12', '30']