python中scipy.optimize.leastsq(最小二乘拟合)用法
python中scipy.optimize.leastsq(最小二乘拟合)用法
《Python程序设计与科学计算》中SciPy.leastsq(最小二乘拟合)的一些笔记。
假设有一组实验数据(xi,yi),已知它们之间的函数关系为y=f(x),通过这些信息,需要确定函数中的一些参数项。例如,如果f是一个线性函数f(x)=kx+b,那么参数k和b就是需要确定的值,得到如下公式中的S函数最小:
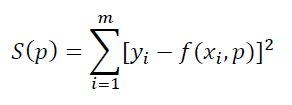
这种算法被称为最小二乘拟合(Least Square Fitting)。
SciPy子函数库optimize已经提供了实现最小二乘拟合算法的函数leastsq。下面的例子使用leastsq,实现最小二乘拟合。
定义数据拟合所用函数:
![]()
import numpy as np
from scipy import linalg
from scipy.optimize import leastsq
def func(x, p):
A, k, theta = p
return A * np.sin(2 * np.pi * k * x + theta)
下面代码是定义计算误差函数,计算实验数据想x、y和拟合函数之间的差,参数p为拟合需要找到的系数,同时添加噪声数据。
def residuals(p, y, x):
return y - func(x, p)
x = np.linspace(0, -2 * np.pi, 100)
A, k, theta = 10, 0.34, np.pi / 6 # 真实数据的函数参数
y0 = func(x, [A, k, theta]) # 真实数据
y1 = y0 + 2 * np.random.randn(len(x)) # 加入噪声之后的实验数据
p0 = [7, 0.2, 0] # 第一次猜测的函数拟合参数
调用leastsq拟合,residuals为计算误差函数,p0为拟合参数初始值,args为需要拟合的实验数据。
plsq = leastsq(residuals, p0, args=(y1, x))
print("真实参数:", [A, k, theta])
print("拟合参数:", plsq[0])
输出:
真实参数: [10, 0.34, 0.5235987755982988]
拟合参数: [10.56295783 0.33945091 0.46569609]
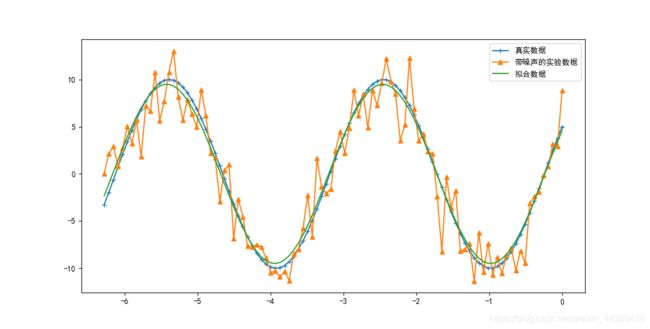
从结果可以看出,最小二乘拟合的结果与真实值之间的误差在可控范围之内,模型具有较好的效果。下面通过绘制图像来观察数据拟合效果,如图1所示。
import matplotlib.pyplot as plt
import pylab as pl
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
pl.plot(x, y0, marker='+', label=u"真实数据")
pl.plot(x, y1, marker='^', label=u"带噪声的实验数据")
pl.plot(x, func(x, plsq[0]), label=u"拟合数据")
pl.legend()
pl.show()
import numpy as np
from scipy import linalg
from scipy.optimize import leastsq
def func(x, p):
A, k, theta = p
return A * np.sin(2 * np.pi * k * x + theta)
def residuals(p, y, x):
return y - func(x, p)
x = np.linspace(0, -2 * np.pi, 100)
A, k, theta = 10, 0.34, np.pi / 6 # 真实数据的函数参数
y0 = func(x, [A, k, theta]) # 真实数据
y1 = y0 + 2 * np.random.randn(len(x)) # 加入噪声之后的实验数据
p0 = [7, 0.2, 0] # 第一次猜测的函数拟合参数
plsq = leastsq(residuals, p0, args=(y1, x))
print("真实参数:", [A, k, theta])
print("拟合参数:", plsq[0])
import matplotlib.pyplot as plt
import pylab as pl
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
pl.plot(x, y0, marker='+', label=u"真实数据")
pl.plot(x, y1, marker='^', label=u"带噪声的实验数据")
pl.plot(x, func(x, plsq[0]), label=u"拟合数据")
pl.legend()
pl.show()
关于leastsq()的说明:
scipy.optimize.leastsq(func, x0, args=(), Dfun=None, full_output=0, col_deriv=0, ftol=1.49012e-08, xtol=1.49012e-08, gtol=0.0, maxfev=0, epsfcn=None, factor=100, diag=None)
参数:
(1)func:callable
应该至少接受一个(可能为N个向量)长度的参数,并返回M个浮点数。它不能返回NaN,否则拟合可能会失败。
func 是我们自己定义的一个计算误差的函数。
(2)x0:ndarray
最小化的起始估算。
x0 是计算的初始参数值。
(3)args:tuple, 可选参数
函数的所有其他参数都放在此元组中。
args 是指定func的其他参数。
一般我们只要指定前三个参数就可以了。
(4)Dfun:callable, 可选参数
一种计算函数的雅可比行列的函数或方法,其中行之间具有导数。如果为None,则将估算雅可比行列式。
(5)full_output:bool, 可选参数
非零可返回所有可选输出。
(6)col_deriv:bool, 可选参数
非零,以指定Jacobian函数在列下计算导数(速度更快,因为没有转置操作)。
(7)ftol:float, 可选参数
期望的相对误差平方和。
(8)xtol:float, 可选参数
近似解中需要的相对误差。
(9)gtol:float, 可选参数
函数向量和雅可比行列之间需要正交。
(10)maxfev:int, 可选参数
该函数的最大调用次数。如果提供了Dfun,则默认maxfev为100 *(N + 1),其中N是x0中的元素数,否则默认maxfev为200 *(N + 1)。
(11)epsfcn:float, 可选参数
用于确定合适的步长以进行雅可比行进的正向差分近似的变量(对于Dfun = None)。通常,实际步长为sqrt(epsfcn)* x如果epsfcn小于机器精度,则假定相对误差约为机器精度。
(12)factor:float, 可选参数
决定初始步骤界限的参数(factor * || diag * x||)。应该间隔(0.1, 100)。
(13)diag:sequence, 可选参数
N个正条目,作为变量的比例因子。
返回值:
(1)x:ndarray
解决方案(或调用失败的最后一次迭代的结果)。
(2)cov_x:ndarray
黑森州的逆。 fjac和ipvt用于构造粗麻布的估计值。无值表示奇异矩阵,这意味着参数x的曲率在数值上是平坦的。要获得参数x的协方差矩阵,必须将cov_x乘以残差的方差-参见curve_fit。
(3)infodict:字典
带有键的可选输出字典:
(4)nfev
函数调用次数
(5)fvec
在输出处评估的函数
(6)fjac
最终近似雅可比矩阵的QR因式分解的R矩阵的排列,按列存储。与ipvt一起,可以估算出估计值的协方差。
(7)ipvt
长度为N的整数数组,它定义一个置换矩阵p,以使fjac * p = q * r,其中r是上三角形,其对角线元素的幅度没有增加。 p的第j列是单位矩阵的ipvt(j)列。
(8)qtf
向量(transpose(q)* fvec)。
(9)mesg:力量
字符串消息,提供有关失败原因的信息。
(10)ier:整型
整数标志。如果等于1、2、3或4,则找到解。否则,找不到解决方案。无论哪种情况,可选输出变量‘mesg’都会提供更多信息。
关于leastsq()的说明转载自:https://vimsky.com/examples/usage/python-scipy.optimize.leastsq.html