机器学习笔记九——线性模型原理以及python实现案例
线性模型
- 1、线性模型概述
- 2 、广义线性模型
- 3、用于回归的线性模型
-
- 3.1 线性回归(又名普通最小二乘法)
-
- 3.1.1 单变量线性回归
- 3.1.2 多变量线性回归
- 3.2 岭回归(ridge regression)
- 3.3 LASSO回归
- 4、用于分类的线性模型
-
- 4.1 对数几率回归(逻辑回归)
- 4.2 线性判别分析(LDA)
1、线性模型概述
给定一个由d个属性描述的实例 x = ( x 1 ; x 2 ; . . . ; x d ) x=(x_1;x_2;...;x_d) x=(x1;x2;...;xd) ,其中 x i x_i xi是
是x在第i个属性上的取值,线性模型(linear model) 的原理是试图学得一个通过属性的线性组合来进行预测的函数,即
f ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ d x d f(x)=\theta_0+\theta_1x_1+\theta_2x_2+...+\theta_dx_d f(x)=θ0+θ1x1+θ2x2+...+θdxd
向量形式:
f ( x ) = θ T X f(x)=\theta^TX f(x)=θTX
其中 θ = ( θ 0 ; θ 1 ; . . . ; θ d ) \theta=(\theta_0;\theta_1;...;\theta_d) θ=(θ0;θ1;...;θd), X = ( 1 , x 1 , x 2 , . . . x d ) X=(1,x_1,x_2,...x_d) X=(1,x1,x2,...xd),权重向量 θ i \theta_i θi 和偏置项 θ 0 \theta_0 θ0是待估计的参数。
线性模型具有良好的可解释性(comprehensibility),每个属性对应的权重可以理解为它对预测的重要性,并且建模较为简单,许多功能更为强大的非线性模型(nonlinear model)都是在线性模型的基础上引入层级结构或高维映射得到的。
2 、广义线性模型
除了直接让模型预测值逼近实值标记 y,我们还可以让它逼近 y 的衍生物,这就是 广义线性模型(generalized linear model) 的思想,即:
y = g − 1 ( ω T x + b ) y=g^{-1}(\omega^Tx+b) y=g−1(ωTx+b)
其中 g(⋅)称为 联系函数(link function),要求单调可微。使用广义线性模型我们可以实现强大的 非线性函数映射 功能。比方说 对数线性回归(log-linear regression),令 g(⋅)=ln(⋅),此时模型预测值对应的是实值标记在指数尺度上的变化:
![]()
广义线性模型的参数估计常通过加权最小二乘法或极大似然法进行。
3、用于回归的线性模型
3.1 线性回归(又名普通最小二乘法)
目的:用于回归,进行预测
- 数据预处理:
一般的线性回归模型要求属性的数据类型为连续值,故需要对离散属性进行连续化。 - 离散属性连续化
分两种情况- 属性值之间有序:也即属性值有明确的大小关系,比方说把二值属性“身高”的取值 {高,矮} 可转化为 {1.0,0.0},三值属性 “高度”的取值 {高,中,低} 转换(编码)为 {1.0,0.5,0.0};
- 属性值之间无序:若该属性有 k个属性值,则通常把它转换为 k 维向量,比方说把无序离散属性 “商品” 的取值 {牙膏,牙刷,毛巾} 转换为 (0,0,1),(0,1,0),(1,0,0)。 这种做法在 自然语言处理和推荐系统 实现中很常见,属性 “单词” 和 “商品” 都是无序离散变量,在建模前往往需要把这样的变量转换为哑变量,否则会引入不恰当的序关系,从而影响后续处理(比如距离的计算)。
![]()
3.1.1 单变量线性回归
样本只有一个属性x,训练集有m个样本。
-
假设函数模型函数):用于预测
f ( x ) = θ 0 + θ 1 x f(x)=\theta_0+\theta_1 x f(x)=θ0+θ1x
为了将f(x)写成向量化的形式(方便编程),可在变量x中添加一列1形成2维向量 X = [ 1 , x ] T X=[1,x]^T X=[1,x]T,参数 θ \theta θ为2维的向量 [ θ 0 , θ 1 ] T [\theta_0,\theta_1]^T [θ0,θ1]T(这里向量指的都是列向量),则 f ( x ) = θ T X f(x)=\theta^TX f(x)=θTX -
代价函数:均方误差,也称平方损失
J ( θ ) = 1 2 m ∑ i = 1 m ( f ( x i ) − y i ) 2 = 1 2 m ∑ i = 1 m ( θ 0 + θ 1 x i − y i ) 2 J(\theta)=\frac{1}{2m}\sum_{i=1}^m(f(x_i)-y_i)^2 \\ =\frac{1}{2m}\sum_{i=1}^m(\theta_0+\theta_1 x_i-y_i)^2 J(θ)=2m1i=1∑m(f(xi)−yi)2=2m1i=1∑m(θ0+θ1xi−yi)2
其中, f ( x i ) f(x_i) f(xi)是第i个样本的预测值, y i y_i yi是第i个样本的真实值,m是数据集D中共有m个样本。前面系数 1 2 m \frac{1}{2m} 2m1是为了求解方便 -
目标函数:
m i n J ( θ ) minJ(\theta) minJ(θ) -
参数估计: θ \theta θ的估计
方法一:最小二乘法
基于均方误差最小化来进行模型求解的一种方法,叫作最小二乘法。
θ ∗ = a r g m i n θ J ( θ ) = a r g m i n θ 1 2 m ∑ i = 1 m ( θ 0 + θ 1 x i − y i ) 2 \theta^*=argmin_{\theta}J(\theta) \\=argmin_{\theta}\frac{1}{2m}\sum_{i=1}^m(\theta_0+\theta_1 x_i-y_i)^2 θ∗=argminθJ(θ)=argminθ2m1i=1∑m(θ0+θ1xi−yi)2- 求解:
通过对损失函数分别求参数 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 的偏导,并且令导数为0,可以得到这两个参数的 闭式(closed-form)解(也即解)
θ 1 = ∑ i = 1 m y i ( x i − x ˉ ) ∑ i = 1 m x i 2 − 1 m ( ∑ i = 1 m x i ) 2 \theta_1=\frac{\sum_{i=1}^my_i(x_i-\bar x)}{\sum_{i=1}^mx_i^2-\frac{1}{m}(\sum_{i=1}^mx_i)^2} θ1=∑i=1mxi2−m1(∑i=1mxi)2∑i=1myi(xi−xˉ)
θ 0 = 1 m ∑ i = 1 m ( y i − θ 1 x i ) \theta_0=\frac{1}{m}\sum_{i=1}^m(y_i-\theta_1 x_i) θ0=m1i=1∑m(yi−θ1xi)
求解过程
方法二:梯度下降法
梯度下降是一个用来求函数最小值的算法。步骤:
1、初始化参数 θ \theta θ(一般为0),初始学习率 α \alpha α(一般可选择尝试0.01,0.03,0.1,0.3…)2、更新参数:
θ j : = θ j − α ∂ ∂ θ j J ( θ ) \theta_j:=\theta_j-\alpha\frac{∂}{∂\theta_j}J(\theta) θj:=θj−α∂θj∂J(θ)即
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( θ 0 + θ 1 x i − y i ) \theta_0:=\theta_0-\alpha\frac{1}{m}\sum_{i=1}^m(\theta_0+\theta_1 x_i-y_i) θ0:=θ0−αm1i=1∑m(θ0+θ1xi−yi)
θ 1 : = θ 1 − α 1 m ∑ i = 1 m ( θ 0 + θ 1 x i − y i ) ∗ x i \theta_1:=\theta_1-\alpha\frac{1}{m}\sum_{i=1}^m(\theta_0+\theta_1 x_i-y_i)*x_i θ1:=θ1−αm1i=1∑m(θ0+θ1xi−yi)∗xi - 求解:
案例一:吴恩达机器学习课程作业—线性回归练习一
数据集:参数变量:人口数;目标值:收益。
问题:基于人口数与收益建立单变量线性回归模型,以预测收益。
方法一:编写程序
第一步:查看数据
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('ex1data1.txt',header=None,names=['population', 'profit'])#读取数据并赋予列名
df.head()#查看前五行
out:
population profit
0 6.1101 17.5920
1 5.5277 9.1302
2 8.5186 13.6620
3 7.0032 11.8540
4 5.8598 6.8233
df.info()#给出样本数据的相关信息概览 :行数,列数,列索引,列非空值个数,列类型,内存占用
df.describe()#简单的统计函数
第二步:查看数据分布,散点图
df.plot(kind='scatter',x='population',y='profit',figsize=(12,8))
out:

第三步:向量化,初始参数 θ \theta θ
1)在原数据集中添加一列1;
2)从数据集中取出前两列作为训练数据特征变量X,最后一列作为训练数据中目标变量y
df.insert(0, 'Ones', 1)#$\theta_0X_0$中X_0等于1
# set X (training data) and y (target variable)
cols = df.shape[1]
'''
pandas.df.iloc函数
官方文档定义为“基于整数位置的索引,用于按位置进行选择。
'''
X = df.iloc[:,0:cols-1]#X是所有行,去掉最后一列
y = df.iloc[:,cols-1:cols]#y是所有行,最后一列
代价函数应该是numpy矩阵,所以我们需要转换X和Y,然后才能使用它们,我们还需要初始化theta
X=np.matrix(X.values)
y=np.matrix(y.values)
theta=np.matrix(np.array([0,0]))#(1,2)矩阵
#可以看下维数
X.shape,y.shape,theta.shape
((97, 2), (97, 1), (1, 2))
第四步:定义代价函数
def computeCost(X, y, theta):
inner = np.power(((X * theta.T) - y), 2)#np.power()函数,多维幂运算
return np.sum(inner) / (2 * len(X))
第五步:建立梯度下降算法
def gradientDescent(X,y,theta,alpha,iters):#特征X,目标变量y,初始化theta,学习率,迭代次数
temp=np.matrix(np.zeros(theta.shape))#初始化参数变量
parameters=int(theta.ravel().shape[1])#待估计参数的个数
cost=np.zeros(iters)#初始化cost1
for i in range(iters):#更新参数$\theta$
error=(X*theta.T)-y
for j in range(parameters):
term=np.multiply(error,X[:,j])
temp[0,j]=theta[0,j]-((alpha/len(X))*np.sum(term))
theta=temp
cost[i]=computeCost(X,y,theta)#计算每次更新的参数所对应的损失。
return theta,cost
第六步:给定一个学习率 α \alpha α,迭代次数,运行gradientDescent函数,可得到最终参数 θ \theta θ
alpha=0.01
iters=1000
g,cost= gradientDescent(X,y,theta,alpha,iters)
g
out
matrix([[-3.24140214, 1.1272942 ]])
则,可得 θ 0 = − 3.24140214 \theta_0=-3.24140214 θ0=−3.24140214, θ 1 = 1.1272942 \theta_1=1.1272942 θ1=1.1272942;则相应的模型函数:
y = − 3.24140214 + 1.1272942 x y=-3.24140214+1.1272942x y=−3.24140214+1.1272942x
第七步:最后,我们可以使用我们拟合的参数计算训练模型的代价函数(误差)。
computeCost(X,y,g)
4.515955503078912
第八步:我们可以绘制线性模型以及数据,直观地看出它的拟合
x=np.linspace(df.population.min(),df.population.max(),100)#np.linspace主要用来创建等差数列,此处用来规划坐标轴
f=g[0,0]+(g[0,1]*x)#预测值
fig,ax=plt.subplots(figsize=(12,8))
ax.plot(x,f,'r',label='Prediction')#展现变量x与f的趋势变化。
ax.scatter(df.population,df.profit,label='Training Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit Vs.Population Size')
plt.show()
out:
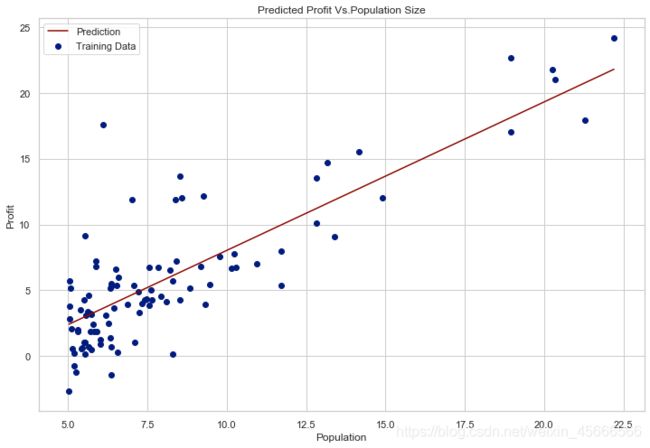
另:由于梯度方程式函数也在每个训练迭代中输出一个代价的向量,所以,我们也可以绘制。请注意,代价总是降低—这是凸优化问题的一个例子
fig,ax=plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters),cost,'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error Vs. Training Epoch')
plt.show()
from sklearn import linear_model
model=linear_model.LinearRegression()
model.fit(X,y)
print("model.coef_:{}".format(model.coef_))#参数w
print("model.intercept_:{}".format(model.intercept_))#截距b
model.coef_:[[0. 1.19303364]]
model.intercept_:[-3.89578088]
绘制线性模型以及数据,直观地看出它的拟合
x=np.array(X[:,1].A1)
f=model.predict(X).flatten()
fig,ax=plt.subplots(figsize=(12,8))
ax.plot(x,f,'r',label='Prediction')
ax.scatter(df.population,df.profit,label='Training Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit Vs.Population Size')
plt.show()
本案例一中所使用数据集如下:
6.1101,17.592
5.5277,9.1302
8.5186,13.662
7.0032,11.854
5.8598,6.8233
8.3829,11.886
7.4764,4.3483
8.5781,12
6.4862,6.5987
5.0546,3.8166
5.7107,3.2522
14.164,15.505
5.734,3.1551
8.4084,7.2258
5.6407,0.71618
5.3794,3.5129
6.3654,5.3048
5.1301,0.56077
6.4296,3.6518
7.0708,5.3893
6.1891,3.1386
20.27,21.767
5.4901,4.263
6.3261,5.1875
5.5649,3.0825
18.945,22.638
12.828,13.501
10.957,7.0467
13.176,14.692
22.203,24.147
5.2524,-1.22
6.5894,5.9966
9.2482,12.134
5.8918,1.8495
8.2111,6.5426
7.9334,4.5623
8.0959,4.1164
5.6063,3.3928
12.836,10.117
6.3534,5.4974
5.4069,0.55657
6.8825,3.9115
11.708,5.3854
5.7737,2.4406
7.8247,6.7318
7.0931,1.0463
5.0702,5.1337
5.8014,1.844
11.7,8.0043
5.5416,1.0179
7.5402,6.7504
5.3077,1.8396
7.4239,4.2885
7.6031,4.9981
6.3328,1.4233
6.3589,-1.4211
6.2742,2.4756
5.6397,4.6042
9.3102,3.9624
9.4536,5.4141
8.8254,5.1694
5.1793,-0.74279
21.279,17.929
14.908,12.054
18.959,17.054
7.2182,4.8852
8.2951,5.7442
10.236,7.7754
5.4994,1.0173
20.341,20.992
10.136,6.6799
7.3345,4.0259
6.0062,1.2784
7.2259,3.3411
5.0269,-2.6807
6.5479,0.29678
7.5386,3.8845
5.0365,5.7014
10.274,6.7526
5.1077,2.0576
5.7292,0.47953
5.1884,0.20421
6.3557,0.67861
9.7687,7.5435
6.5159,5.3436
8.5172,4.2415
9.1802,6.7981
6.002,0.92695
5.5204,0.152
5.0594,2.8214
5.7077,1.8451
7.6366,4.2959
5.8707,7.2029
5.3054,1.9869
8.2934,0.14454
13.394,9.0551
5.4369,0.61705
案例二:
wave数据集形成一个单变量线性回归模型
wave数据集只有一个输入特征
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import mglearn
%matplotlib inline
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
X,y=mglearn.datasets.make_wave(n_samples=60)
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=42)
lr=LinearRegression().fit(X_train,y_train)
print("lr.coef_:{}".format(lr.coef_))#参数w
print("lr.intercept_:{}".format(lr.intercept_))#截距b
#训练集和测试集的性能
print("训练集得分:{:.2f}".format(lr.score(X_train,y_train)))
print("测试集得分:{:.2f}".format(lr.score(X_test,y_test)))
lr.coef_:[0.39390555]
lr.intercept_:-0.031804343026759746
训练集得分:0.67
测试集得分:0.66
模型函数: y = 0.39390555 x − 0.031804343026759746 y=0.39390555x-0.031804343026759746 y=0.39390555x−0.031804343026759746
模型分析:测试集得分即 R 2 R^2 R2约为0.66,效果不是很好,但测试集和训练集得分非常接近,这说明可能存在欠拟合,而不是过拟合。
3.1.2 多变量线性回归
多变量线性回归,又称多元线性回归
样本有多个属性
-
假设(模型)函数:用于预测
f ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n f(x)=\theta_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n f(x)=θ0+θ1x1+θ2x2+...+θnxn
为了将f(x)写成向量化的形式(方便编程),可在变量x中添加一列1形成n+1维向量 X = [ 1 , x 1 , x 2 , . . . , x n ] T X=[1,x_1,x_2,...,x_n]^T X=[1,x1,x2,...,xn]T,参数 θ \theta θ为n+1维的向量 [ θ 0 , θ 1 , . . . , θ n ] T [\theta_0,\theta_1,...,\theta_n]^T [θ0,θ1,...,θn]T(这里向量指的都是列向量),则 f ( x ) = θ T X f(x)=\theta^TX f(x)=θTX -
代价函数:均方误差,也称平方损失
J ( θ ) = 1 2 m ( θ T X − y ) 2 = 1 2 m ∑ i = 1 m ( θ T x i − y i ) 2 J(\theta)=\frac{1}{2m}({\theta}^TX-y)^2=\frac{1}{2m}\sum_{i=1}^m({\theta}^Tx_i-y_i)^2 J(θ)=2m1(θTX−y)2=2m1i=1∑m(θTxi−yi)2
其中, f ( x i ) f(x_i) f(xi)是第i个样本的预测值, y i y_i yi是第i个样本的真实值,m是数据集D中共有m个样本。 -
目标函数:
m i n J ( θ ) minJ(\theta) minJ(θ) -
参数估计: θ \theta θ的估计
方法一:最小二乘法
基于均方误差最小化来进行模型求解的一种方法,叫作最小二乘法。
θ ∗ = a r g m i n θ 1 2 m ∑ i = 1 m ( θ T x i − y i ) 2 {\theta}^*=argmin_{\theta}\frac{1}{2m}\sum_{i=1}^m({\theta}^Tx_i-y_i)^2 θ∗=argminθ2m1i=1∑m(θTxi−yi)2- 求解:
通过对损失函数分别求参数 ω \omega ω 和b 的偏导,并且令导数为0,可以得到这两个参数的 闭式(closed-form)解(也即解)
θ ∗ = ( X T X ) − 1 X T y \theta^*=(X^TX) ^{−1}X ^Ty θ∗=(XTX)−1XTy
求解过程
注: 这就要求 X T X X^TX XTX必须是可逆矩阵,也即必须是满秩矩阵(full-rank matrix) 或者是 正定矩阵(positive definite matrix),但是!现实任务中 X T X X^TX XTX 往往不是满秩的,很多时候 X的列数很多,甚至超出行数(例如 推荐系统,商品数是远远超出用户数的),此时 X T X X^TX XTX显然不满秩,会解出多个 w ^ \hat{w} w^这些解都能使得均方误差最小化,选择哪一个解作为输出,这时就需要由学习算法的归纳偏好决定了,常见的做法是引入 正则化项。
方法二:梯度下降法
梯度下降是一个用来求函数最小值的算法。步骤:
1、初始化参数 θ \theta θ(一般为0),初始学习率 α \alpha α(一般可选择尝试0.01,0.03,0.1,0.3…)2、当多个特征即属性的单位不一致时,需要进行特征缩放: x = x − μ s x=\frac{x-\mu}{s} x=sx−μ
3、更新参数:
θ j : = θ j − α ∂ ∂ θ j J ( θ ) = θ j − α ∂ ∂ θ j 1 2 m ∑ i = 1 m ( θ T x i − y i ) 2 \theta_j:=\theta_j-\alpha\frac{∂}{∂\theta_j}J(\theta)=\theta_j-\alpha\frac{∂}{∂\theta_j}\frac{1}{2m}\sum_{i=1}^m({\theta}^Tx_i-y_i)^2 θj:=θj−α∂θj∂J(θ)=θj−α∂θj∂2m1i=1∑m(θTxi−yi)2即
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( θ T x i − y i ) \theta_0:=\theta_0-\alpha\frac{1}{m}\sum_{i=1}^m(\theta^T x_i-y_i) θ0:=θ0−αm1i=1∑m(θTxi−yi)
当j>=1时:
θ j : = θ j − α 1 m ∑ i = 1 m ( θ T x i − y i ) ∗ x i j \theta_j:=\theta_j-\alpha\frac{1}{m}\sum_{i=1}^m(\theta^Tx_i-y_i)*x_{ij} θj:=θj−αm1i=1∑m(θTxi−yi)∗xij其中, x i x_i xi是数据集中的第i个样本, x i j x_ij xij是数据集中的第i个样本第j个属性的取值。
- 求解:
案例一:吴恩达机器学习课程作业—线性回归练习二
数据集有2个变量(房子的大小,卧室的数量)和目标(房子的价格)。对其建立多变量线性回归模型。
方法与单变量线性回归中案例一一样。只不过这里多了一个特征缩放步骤。
1、查看数据
path='ex1data2.txt'
data2=pd.read_csv(path,header=None,names=['Size','Bedrooms','Price'])
data2.head()#查看前五行数据
Size Bedrooms Price
0 2104 3 399900
1 1600 3 329900
2 2400 3 369000
3 1416 2 232000
4 3000 4 539900
2、特征缩放
data2=(data2-data2.mean())/data2.std()
data2.head()
3、第三步:向量化,初始参数 θ \theta θ
1)在原数据集中添加一列1;
2)从数据集中取出前两列作为训练数据特征变量X,最后一列作为训练数据中目标变量y
# 添加一列
data2.insert(0,'Ones',1)
data2.head()#查看前五行
#取训练集X2,目标变量y2
cols=data2.shape[1]#求列数
X2=data2.iloc[:,0:cols-1]
y2=data2.iloc[:,cols-1:cols]
#X2,y2转换成矩阵形式并初始化theta
X2=np.matrix(X2.values)
y2=np.matrix(y2.values)
theta2=np.matrix(np.array([0,0,0]))
4、定义代价函数、梯度下降算法与前面的一样,这里直接引用,计算参数,代价函数
g2,cost2=gradientDescent(X2,y2,theta2,alpha,iters)
g2
matrix([[-1.10868761e-16, 8.78503652e-01, -4.69166570e-02]])
computeCost(X2,y2,g2)
0.13070336960771892
本案例中所使用数据集如下:
2104,3,399900
1600,3,329900
2400,3,369000
1416,2,232000
3000,4,539900
1985,4,299900
1534,3,314900
1427,3,198999
1380,3,212000
1494,3,242500
1940,4,239999
2000,3,347000
1890,3,329999
4478,5,699900
1268,3,259900
2300,4,449900
1320,2,299900
1236,3,199900
2609,4,499998
3031,4,599000
1767,3,252900
1888,2,255000
1604,3,242900
1962,4,259900
3890,3,573900
1100,3,249900
1458,3,464500
2526,3,469000
2200,3,475000
2637,3,299900
1839,2,349900
1000,1,169900
2040,4,314900
3137,3,579900
1811,4,285900
1437,3,249900
1239,3,229900
2132,4,345000
4215,4,549000
2162,4,287000
1664,2,368500
2238,3,329900
2567,4,314000
1200,3,299000
852,2,179900
1852,4,299900
1203,3,239500
案例二:
波士顿房价数据集形成一个多变量线性回归模型
波士顿房价数据集有506个样本和105个导出特征
X,y=mglearn.datasets.load_extended_boston()
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=42)
lr=LinearRegression().fit(X_train,y_train)
print("lr.coef_:{}".format(lr.coef_))#参数w
print("lr.intercept_:{}".format(lr.intercept_))#截距b
#训练集和测试集的性能
print("训练集得分:{:.2f}".format(lr.score(X_train,y_train)))
print("测试集得分:{:.2f}".format(lr.score(X_test,y_test)))
lr.coef_:[-5.11126504e+02 4.02559787e+00 -9.45778613e+01 1.34720251e+01
…
3.50306579e+00 -5.10021527e+00 2.46929457e+00 2.55749022e+01]
lr.intercept_:-34.707522103873494
训练集得分:0.94
测试集得分:0.78
参数是一个多维数组
模型分析:测试集得分即 R 2 R^2 R2约为0.61,效果不是很好,又测试集和训练集得分即性能差异过大,这说明可能存在过拟合。
为了解决过拟合现象,提出了岭回归模型与LASSO回归;标准线性回归最常用的替代方法之一就是岭回归。
scikit-learn中线性回归模块用法
岭回归与Lasso回归的出现是为了解决线性回归出现的过拟合以及在通过正规方程方法求解θ的过程中出现的x转置乘以x不可逆这两类问题的,这两种回归均通过在损失函数中引入正则化项来达到目的,具体三者的损失函数对比见下图:
![]()
其中λ称为正则化参数,如果λ选取过大,会把所有参数θ均最小化,造成欠拟合,如果λ选取过小,会导致对过拟合问题解决不当,因此λ的选取是一个技术活。
岭回归与Lasso回归最大的区别在于岭回归引入的是L2范数惩罚项,Lasso回归引入的是L1范数惩罚项,Lasso回归能够使得损失函数中的许多θ均变成0,这点要优于岭回归,因为岭回归是要所有的θ均存在的,这样计算量Lasso回归将远远小于岭回归。
3.2 岭回归(ridge regression)
在线性回归模型中,其参数估计公式为 w ∗ ^ = ( X T X ) − 1 X T y \hat{w^∗}=(X^TX) ^{−1}X ^Ty w∗^=(XTX)−1XTy,当 X T X X^TX XTX不可逆时无法求出 w ∗ ^ \hat{w^∗} w∗^,另外如果 ∣ X T X ∣ |X^TX| ∣XTX∣越趋近于0,会使得回归系数趋向于无穷大,此时得到的回归系数是无意义的。解决这类问题可以使用岭回归和LASSO回归,同时两者都可解决过拟合问题,主要针对自变量之间存在多重共线性或者自变量个数多于样本量的情况。
1、过拟合
当样本特征很多,样本数相对较少时,模型容易陷入过拟合。为了缓解过拟合问题,有两种方法:
方法一:减少特征数量(人工选择重要特征来保留,会丢弃部分信息)。
方法二:正则化(减少特征参数 ω \omega ω的数量级)。
2、正则化(Regularization)
正则化是结构风险(损失函数+正则化项)最小化策略的体现,是在经验风险(平均损失函数)上加一个正则化项 λ f ( ω ) \lambda f(\omega) λf(ω)即参数的一个函数,其中 λ \lambda λ称为正则化参数。正则化的作用就是选择经验风险和模型复杂度同时较小的模型。
正则化的基本思想是减小高次项的参数的值。
防止过拟合的原理:如果我们令 λ \lambda λ的值很大的话,为了使损失函数尽可能的小,所有的参数 ω \omega ω的值都会在一定程度上减小。
正则化项可以是模型参数向量的范数,经常用的有L1范数,L2范数
L 1 L_1 L1范数:
∣ ∣ x ∣ ∣ 1 = ∑ i = 1 m x i ||x||_1=\sum_{i=1}^mx_i ∣∣x∣∣1=i=1∑mxi
L 2 L_2 L2范数:
∣ ∣ x ∣ ∣ 2 = ∑ i = 1 m x i 2 ||x||_2=\sqrt{\sum_{i=1}^mx_i^2} ∣∣x∣∣2=i=1∑mxi2
3、岭回归
岭回归就是使用 L 2 L_2 L2范数正则化的线性回归,使得每一个参数减小,以使每一个特征对输出结果的影响减小。
岭回归与线性回归的区别是代价函数不一样:在线性回归代价函数上加上参数向量的正则化项。
模型函数:与线性回归一样
代价函数:
J ( ω ^ ) = 1 2 m [ ∑ i = 1 m ( y i − ω ^ T x i ) 2 + λ ∣ ∣ ω ∣ ∣ 2 2 ] = 1 2 m [ ∑ i = 1 m ( y i − ω ^ T x i ) 2 + λ ∑ j = 1 n ω j 2 ] J(\hat\omega)=\frac{1}{2m}[\sum_{i=1}^m(y_i-\hat{\omega}^Tx_i)^2+\lambda||\omega||_2^2]\\=\frac{1}{2m}[\sum_{i=1}^m(y_i-\hat{\omega}^Tx_i)^2+\lambda\sum_{j=1}^n\omega_j^2] J(ω^)=2m1[i=1∑m(yi−ω^Txi)2+λ∣∣ω∣∣22]=2m1[i=1∑m(yi−ω^Txi)2+λj=1∑nωj2]
其中λ称为正则化参数,如果λ选取过大,会把所有参数θ均最小化,造成欠拟合,如果λ选取过小,会导致对过拟合问题解决不当,因此λ的选取是一个技术活。
参数估计:
1、梯度下降法:
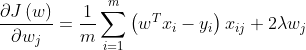
迭代公式如下:
2、方程求解:
最优解为:
![]()
最后,将学得的线性回归模型为:
![]()
λ的选择
- 模型的方差:回归系数的方差
- 模型的偏差:预测值和真实值的差异
随着模型复杂度的提升,在训练集上的效果就越好,即模型的偏差就越小;但是同时模型的方差就越大。对于岭回归的 λ \lambda λ而言,随着 λ \lambda λ的增大, ∣ X T X + λ I ∣ |X^TX+\lambda I| ∣XTX+λI∣ 就越大, ( X T X + λ I ) − 1 (X^T X+λI) ^{−1} (XTX+λI)−1就越小,模型的方差就越小;而 λ \lambda λ越大使得 ω \omega ω的估计值更加偏离真实值,模型的偏差就越大。所以岭回归的关键是找到一个合理的 λ \lambda λ值来平衡模型的方差和偏差。
案例: 波士顿房价数据集形成一个多变量线性回归模型
from sklearn.linear_model import Ridge
ridge=Ridge().fit(X_train,y_train)#参数默认为1
print("训练集得分:{:.2f}".format(ridge.score(X_train,y_train)))
print("测试集得分:{:.2f}".format(ridge.score(X_test,y_test)))
训练集得分:0.87
测试集得分:0.81
可以看出,岭回归在训练集上的分数要低于线性回归,但在测试上的分数更高。这和我们的预期一样,线性回归对数据存在过拟合。
3.3 LASSO回归
岭回归无法剔除变量,而LASSO回归模型,将惩罚项由L2范数变为L1范数,可以将一些不重要的回归系数缩减为0,达到剔除变量的目的。
模型函数:与线性回归一样
代价函数:
J ( ω ^ ) = 1 2 m [ ∑ i = 1 m ( y i − ω ^ T x i ) 2 + λ ∣ ∣ ω ∣ ∣ 1 ] = 1 2 m [ ∑ i = 1 m ( y i − ω ^ T x i ) 2 + λ ∑ j = 1 n ∣ ω j ∣ ] J(\hat\omega)=\frac{1}{2m}[\sum_{i=1}^m(y_i-\hat{\omega}^Tx_i)^2+\lambda||\omega||_1]\\=\frac{1}{2m}[\sum_{i=1}^m(y_i-\hat{\omega}^Tx_i)^2+\lambda\sum_{j=1}^n|\omega_j|] J(ω^)=2m1[i=1∑m(yi−ω^Txi)2+λ∣∣ω∣∣1]=2m1[i=1∑m(yi−ω^Txi)2+λj=1∑n∣ωj∣]
目标函数:
m i n J ( ω ^ ) minJ(\hat\omega) minJ(ω^)
参数估计:
由于 L 1 L_1 L1范数用的是绝对值,导致LASSO的优化目标不是连续可导的,也就是说,最小二乘法,梯度下降法,牛顿法,拟牛顿法都不能用。
L 1 L_1 L1正则化问题求解可采用近端梯度下降法(Proximal Gradient Descent,PGD)。
具体求解见西瓜书P253。
案例:Lasso应用在波士顿数据集上:
from sklearn.linear_model import Lasso
lasso=Lasso().fit(X_train,y_train)
print("训练集得分:{:.2f}".format(lasso.score(X_train,y_train)))
print("测试集得分:{:.2f}".format(lasso.score(X_test,y_test)))
print("使用的特征个数:{}".format(np.sum(lasso.coef_!=0)))
训练集得分:0.27
测试集得分:0.26
使用的特征个数:3
发现,默认alpha即 λ \lambda λ的值为1时,Lasso在训练集与测试集上的表现都很差,这表示存在欠拟合,特征的个数过少,选取 λ \lambda λ的值过大,应该尝试减小 λ \lambda λ的值。
lasso001=Lasso(alpha=0.01).fit(X_train,y_train)
print("训练集得分:{:.2f}".format(lasso001.score(X_train,y_train)))
print("测试集得分:{:.2f}".format(lasso001.score(X_test,y_test)))
print("使用的特征个数:{}".format(np.sum(lasso001.coef_!=0)))
训练集得分:0.89
测试集得分:0.80
使用的特征个数:34
此时,稍微好一点。
注意:如果把alpha设得过小,那么就会消除正则化的效果,并出现过拟合现象。
在实际实践中,在两个模型中一般首选岭回归。但如果特征很多,你认为只有其中几个是重要的,那么选择Lasso可能更好。
4、用于分类的线性模型
4.1 对数几率回归(逻辑回归)
逻辑回归由于存在易于实现、解释性好以及容易扩展等优点,被广泛应用于点击率预估(CTR)、计算广告(CA)以及推荐系统(RS)等任务中。逻辑回归虽然名字叫做回归,但实际上却是一种分类学习方法。
线性回归完成的是回归拟合任务,而对于分类任务,我们同样需要一条线,但不是去拟合每个数据点,而是把不同类别的样本区分开来。

目的: 监督学习,解决二分类问题
对于二分类问题, y ∈ { 0 , 1 } y\in{\{0,1\}} y∈{0,1},1表示正例,0表示负例。逻辑回归是在线性函数 θ T x \theta^Tx θTx输出预测实际值的基础上,寻找一个假设函数 h θ ( x ) = g ( θ T x ) h_\theta(x)=g(\theta^Tx) hθ(x)=g(θTx),将实际值映射到到0,1之间 ,如果 h θ ( x ) > = 0.5 h_\theta(x)>=0.5 hθ(x)>=0.5,则预测y=1,及y属于正例;如果 h θ ( x ) < 0.5 h_\theta(x)<0.5 hθ(x)<0.5,则预测y=0,即y属于负例。
逻辑回归中选择对数几率函数(logistic function)作为激活函数,对数几率函数是Sigmoid函数(形状为S的函数)的重要代表。对数几率函数(Sigmoid函数)在一定程度上近似单位阶跃函数的替代函数,并且单调连续可微,
模型函数:
h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}} hθ(x)=g(θTx)=1+e−θTx1
其中 θ \theta θ是参数向量。对于 h θ ( x ) h_\theta(x) hθ(x)的直观解释是:对于给定的输入x, h θ ( x ) h_\theta(x) hθ(x)表示其对应类别y=1即属于正例的概率。
问:为什么逻辑回归又叫对数几率回归?
答:上式可以变化为
ln h θ ( x ) 1 − h θ ( x ) = θ T x \ln\frac{h_\theta(x)}{1-h_\theta(x)}=\theta^Tx ln1−hθ(x)hθ(x)=θTx
h θ ( x ) h_\theta(x) hθ(x)是x属于正例的概率, 1 − h θ ( x ) 1-h_\theta(x) 1−hθ(x)是x属于反例的概率,两者比值 h θ ( x ) 1 − h θ ( x ) \frac{h_\theta(x)}{1-h_\theta(x)} 1−hθ(x)hθ(x)叫做几率(odds),表示了x作为正例的相对可能性。。取对数就叫做对数几率(log odds,或logit) ln h θ ( x ) 1 − h θ ( x ) \ln\frac{h_\theta(x)}{1-h_\theta(x)} ln1−hθ(x)hθ(x)
如果说线性回归是对于特征的线性组合来拟合真实标记的话( y = ω x + b y=\omega x+b y=ωx+b),那么逻辑回归是对于特征的线性组合来拟合真实标记为正例的概率的对数几率( ln y 1 − y = w x + b \ln{\frac{y}{1-y}}=wx+b ln1−yy=wx+b )
对于输入x分类结果为类别1和类别0的概率分别为:
P ( y = 1 ∣ x ; θ ) = h θ ( x ) P(y=1|x;\theta)=h_\theta(x) P(y=1∣x;θ)=hθ(x)
P ( y = 0 ∣ x ; θ ) = 1 − h θ ( x ) . P(y=0|x;\theta)=1-h_\theta(x). P(y=0∣x;θ)=1−hθ(x).
例如,如果对于给定的x,通过已经确定的参数计算得出 h θ ( x ) = 0.7 h_\theta(x)=0.7 hθ(x)=0.7,则表示有70%的几率y为正例,相应的y为负例的几率为0.3。
决策边界:
在逻辑回归中,我们预测:
- 当 h θ h_\theta hθ大于等于0.5时,预测类别y=1;
- 当 h θ h_\theta hθ小于0.5时,预测类别y=0;
根据上面绘制出的S形函数图像,
又 z = θ T x z=\theta^Tx z=θTx
则:
- θ T x \theta^Tx θTx大于等于0时,预测类别y=1;
- θ T x \theta^Tx θTx小于0时,预测类别y=0.
假设我们有一个模型: h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 ) h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2) hθ(x)=g(θ0+θ1x1+θ2x2)
并且参数 θ \theta θ是向量[-3 1 1]。
则当 − 3 + x 1 + x 2 −3+x1+x2 −3+x1+x2大于等于0,即 x 1 + x 2 x_1+x_2 x1+x2 大于等于3时,模型将预测y=1。绘制直线x1+x2=3,这条线便是我们模型的分界线,将预测为1的区域和预测为0的区域分隔开。

其实,LR 模型就是在拟合 z = w T x + b = 0 z = w^T x +b=0 z=wTx+b=0 这条直线,使得这条直线尽可能地将原始数据中的两个类别正确的划分开。
损失函数:
J ( θ ) = 1 m ∑ i = 1 m C o s t ( h θ ( x ( i ) ) , y ( i ) ) = − 1 m ∑ i = 1 m [ y ( i ) log h θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J(\theta)=\frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}),y^{(i)}) \\ = -\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}\log{h_\theta(x^{(i)})}+(1-y^{(i)})\log{(1-h_\theta(x^{(i)}))}] J(θ)=m1∑i=1mCost(hθ(x(i)),y(i))=−m1∑i=1m[y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
其中, y ( i ) y^{(i)} y(i)是第i个样本的真实类别, h θ ( x ( i ) ) h_\theta(x^{(i)}) hθ(x(i))是第i个样本的预测类别。
这个损失函数通常称作为 对数损失 (logloss)或交叉熵损失,这里的对数底为自然对数 e ,其中真实值 y 是有 0/1 两种情况,而推测值 h θ ( x ( i ) ) h_\theta(x^{(i)}) hθ(x(i)) 由于借助对数几率函数,其输出是介于0~1之间连续概率值。仔细查看,不难发现,当真实值 y=0 时,第一项为0,当真实值 y=1 时,第二项为0,所以,这个损失函数其实在每次计算时永远都只有一项在发挥作用,那这不就可以转换为分段函数了吗,分段的形式如下:
C o s t ( h θ ( x ( i ) ) , y ( i ) ) = { − log h θ ( x ( i ) ) y=1 − log ( 1 − h θ ( x ( i ) ) y=0 Cost(h_\theta(x^{(i)}),y^{(i)})= \begin{cases} -\log{h_\theta(x^{(i)})}& \text{y=1}\\ -\log{(1-h_\theta(x^{(i)})}& \text{y=0} \end{cases} Cost(hθ(x(i)),y(i))={−loghθ(x(i))−log(1−hθ(x(i))y=1y=0
问:为什么定义这样的损失函数?
答:实际上 J ( θ ) J(\theta) J(θ)是通过极大似然估计推导得到的
由于y只能取0或1,服从伯努利分布 h θ ( x ) h_\theta(x) hθ(x)是y=1即事件的发生概率,则概率质量函数为
p ( y ∣ x ; θ ) = ( h θ ( x ) ) y ( 1 − h θ ( x ) ) 1 − y p(y|x;\theta)=(h_\theta(x))^y(1-h_\theta(x))^{1-y} p(y∣x;θ)=(hθ(x))y(1−hθ(x))1−y
似然函数:
对于m个独立同分布的训练样本x,其似然函数写作
L ( θ ) = ∏ i = 1 m p ( y ∣ x ; θ ) = ∏ i = 1 m h θ ( x i ) y i ( 1 − h θ ( x i ) ) 1 − y i L(\theta)=\prod^{m}_{i=1}p(y|x;\theta)=\prod^{m}_{i=1}h_\theta(x_i)^{y_i}(1-h_\theta(x_i))^{1-y_i} L(θ)=∏i=1mp(y∣x;θ)=∏i=1mhθ(xi)yi(1−hθ(xi))1−yi
对数似然函数:
l ( θ ) = l o g L ( θ ) = ∑ i = 1 m y i log h θ ( x i ) + ( 1 − y i ) log ( 1 − h θ ( x i ) ) l(θ)=logL(θ)= \sum_{i=1}^my_i\log{h_\theta(x_i)}+(1-y_i)\log{(1-h_\theta(x_i))} l(θ)=logL(θ)=i=1∑myiloghθ(xi)+(1−yi)log(1−hθ(xi))
最大化对数似然函数求 θ \theta θ,相当于最小化对数似然函数的相反数。
故定义损失函数 J ( θ ) J(\theta) J(θ)为
J ( θ ) = − 1 m l ( θ ) J(θ)=−\frac{1}{m}l(θ) J(θ)=−m1l(θ)
目标函数:
m i n θ J ( θ ) min_{\theta}J(\theta) minθJ(θ)
参数估计:
参用梯度下降法利用梯度下降法更新 θ \theta θ,求最优参数。
θ j : = θ j − α ∂ ∂ θ j J ( θ ) = θ j − α ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j:=\theta_j-\alpha\frac{∂}{∂\theta_j}J(\theta)=\theta_j-\alpha\sum_{i=1}^m(h _θ(x ^{(i)})-y^{(i)})x_j^{(i)} θj:=θj−α∂θj∂J(θ)=θj−αi=1∑m(hθ(x(i))−y(i))xj(i)
其中 x j ( i ) x_j^{(i)} xj(i)是第i个样本x的第j个属性的取值。
推导过程:

虽然得到的梯度下降更新迭代公式看上去与线性回归的梯度下降算法一样,但是这里的 h θ ( x ) = g ( θ T x ) h_\theta(x)=g(\theta^Tx) hθ(x)=g(θTx) 与线性回归不同,所以实际上是不一样的。除了梯度下降法,还有其他的一些用来求代价函数最小时参数θ\thetaθ的方法,如牛顿法、共轭梯度法(Conjugate Gradietn)、局部优化法(BFGS)和有限内存局部优化法(LBFGS)等。
损失函数:
对于逻辑回归损失函数加入正则项得:
J ( θ = − 1 m ∑ i = 1 m [ y ( i ) log h θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta= -\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}\log{h_\theta(x^{(i)})}+(1-y^{(i)})\log{(1-h_\theta(x^{(i)}))}]+\frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2 J(θ=−m1∑i=1m[y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]+2mλ∑j=1nθj2
注:根据惯例,不对 θ 0 \theta_0 θ0 进行惩罚。
其中 λ \lambda λ叫做正则化参数,用于平衡拟合训练数据和保持参数值较小避免过拟合之间的关系。
如果 λ \lambda λ过大,则决策边界会趋于一条直线

参数估计:
梯度下降法更新参数
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) \theta_0:=\theta_0-\alpha\frac{1}{m}\sum_{i=1}^m(h _θ(x ^{(i)})-y^{(i)})x_0^{(i)} θ0:=θ0−αm1i=1∑m(hθ(x(i))−y(i))x0(i)
θ j : = θ j − α 1 m ∑ i = 1 m [ ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] , j = 1 , 2 , . . . \theta_j:=\theta_j-\alpha\frac{1}{m}\sum_{i=1}^m[(h _θ(x ^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda}{m}\theta_j], j=1,2,... θj:=θj−αm1i=1∑m[(hθ(x(i))−y(i))xj(i)+mλθj],j=1,2,...
上去形式跟正则化线性回归一样,但其中 h θ ( x ) = g ( θ T x ) h_\theta(x)=g(\theta^Tx) hθ(x)=g(θTx),所以与正则化线性回归不同。
案例一:吴恩达课程练习二
在训练的初始阶段,我们将要构建一个逻辑回归模型来预测,某个学生是否被大学录取。设想你是大学相关部分的管理者,想通过申请学生两次测试的评分,来决定他们是否被录取。现在你拥有之前申请学生的可以用于训练逻辑回归的训练样本集。对于每一个训练样本,你有他们两次测试的评分和最后是被录取的结果。为了完成这个预测任务,我们准备构建一个可以基于两次测试评分来评估录取可能性的分类模型。
第一步:加载、查看数据
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
path='ex2data1.txt'#数据名称
data=pd.read_csv(path,header=None,names=['Exam 1','Exam 2','Admitted'])
data.head()#查看前五行
Exam 1 Exam 2 Admitted
0 34.623660 78.024693 0
1 30.286711 43.894998 0
2 35.847409 72.902198 0
3 60.182599 86.308552 1
4 79.032736 75.344376 1
第二步:查看数据分布,散点图
positive=data[data['Admitted'].isin([1])]
negative=data[data['Admitted'].isin([0])]
fig,ax=plt.subplots(figsize=(12,8))
ax.scatter(positive['Exam 1'],positive['Exam 2'],s=50,c='b',marker='o',label='Admitted')
ax.scatter(negative['Exam 1'],negative['Exam 2'],s=50,c='r',marker='x',label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
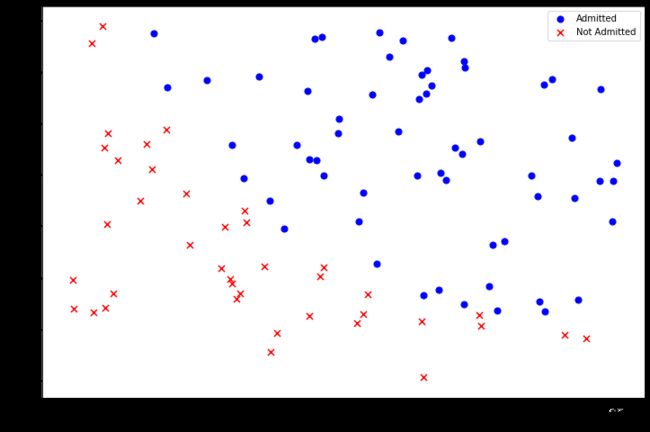
看起来在两类间,有一个清晰的决策边界,接下来实现逻辑回归,训练一个模型来预测结果。
第三步:数据预处理,向量化,指定特征变量X,目标变量y
data.insert(0,'ones',1)#添加一列1,对应截距的参数
cols=data.shape[1]#列数
X=data.iloc[:,0:cols-1]
y=data.iloc[:,cols-1:cols]
X=np.array(X.values)
y=np.array(y.values)
theta=np.zeros(3)
X.shape,theta.shape,y.shape#检查维数
第四步:定义代价函数、建立梯度下降算法
def sigmoid(z):#sigmoid函数
return 1/(1+np.exp(-z))
def cost(theta,X,y):
theta=np.matrix(theta)
X=np.matrix(X)
y=np.matrix(y)
first=np.multiply(-y,np.log(sigmoid(X*theta.T)))
second=np.multiply((1-y),np.log(1-sigmoid(X*theta.T)))
return np.sum(first-second)/len(X)
#梯度下降算法
def gradient(theta,X,y):
theta=np.matrix(theta)
X=np.matrix(X)
y=np.matrix(y)
parameters=int(theta.ravel().shape[1])
grad=np.zeros(parameters)
error=sigmoid(X*theta.T)-y
for i in range(parameters):
term=np.multiply(error,X[:,i])
grad[i]=np.sum(term)/len(X)
return grad
注意,我们实际上没有在这个gradient函数中执行梯度下降,我们仅仅在计算一个梯度步长grad。 在练习中,一个称为“fminunc”的Octave函数是用来优化函数来计算成本和梯度参数。 由于我们使用Python,我们可以用SciPy的“optimize”命名空间来做同样的事情。
第五步:用SciPy’s truncated newton(TNC)实现寻找最优参数。
import scipy.optimize as opt
result=opt.fmin_tnc(func=cost,x0=theta,fprime=gradient,args=(X,y))
result
(array([-25.16131872, 0.20623159, 0.20147149]), 36, 0)
第六步:查看最终代价
cost(result[0], X, y)
第七步:预测,进行分类,模型的准确率 。
如果 h θ ( x ) > = 0.5 h_\theta(x)>=0.5 hθ(x)>=0.5,则预测y=1,及y属于正例;如果 h θ ( x ) < 0.5 h_\theta(x)<0.5 hθ(x)<0.5,则预测y=0,即y属于负例。**
def predict(theta, X):
probability = sigmoid(X * theta.T)
return [1 if x >= 0.5 else 0 for x in probability]
#模型的准确率
theta_min = np.matrix(result[0])
predictions = predict(theta_min, X)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
accuracy = (sum(map(int, correct)) % len(correct))
print ('accuracy = {0}%'.format(accuracy))
案例:forge数据集上运用LR模型
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
X,y=mglearn.datasets.make_forge()
fig,axes=plt.subplots(1,2,figsize=(10,3))
for model,ax in zip([LinearSVC(),LogisticRegression()],axes):
clf=model.fit(X,y)
mglearn.plots.plot_2d_separator(clf,X,fill=False,eps=0.5,ax=ax,alpha=.7)
mglearn.discrete_scatter(X[:,0],X[:,1],y,ax=ax)
ax.set_title("{}".format(clf.__class__.__name__))
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
此LR默认使用L2正则化。
4.2 线性判别分析(LDA)
解决二分类问题。
线性判别分析(Linear Discriminant Analysis,简称LDA),同样是利用线性模型,LDA提供一种不同的思路。在LDA中,我们不再是拟合数据分布的曲线,而是 将所有的数据点投影到一条直线上,使得 同类点的投影尽可能近,不同类点的投影尽可能远。二分类LDA最早有Fisher提出,因此也称为 Fisher判别分析。
![]()
具体来说,投影值 , y = ω T x y=\omega^Tx y=ωTx我们不再用 y 逼近样例的真实标记,而是希望同类样例的投影值尽可能相近,异类样例的投影值尽可能远离。
如何实现呢?
给定数据集 D = ( x i , y i ) i = 1 m , y i ∈ 0 , 1 , D={{(x_i,y_i)}_{i=1}^m},y_i\in{{0,1}}, D=(xi,yi)i=1m,yi∈0,1,令 X i , μ i , ∑ i X_i,\mu_i,\sum_i Xi,μi,∑i分别表示第 i ∈ 0 , 1 i\in{0,1} i∈0,1类示例的集合、均值向量、协方差矩阵。若将数据集投影到直线 ω \omega ω上,则两类样本的中心在直线上的投影分别为 ω T μ 0 \omega^T\mu_0 ωTμ0和 ω T μ 1 \omega^T\mu_1 ωTμ1;若将所有样本点都投影到直线上,则两类样本的协方差分别为 ω T ∑ 0 ω \omega^T\sum_0\omega ωT∑0ω和 ω T ∑ 1 ω \omega^T\sum_1\omega ωT∑1ω。
- 首先,同类样例的投影值尽可能相近意味着同类样例投影值的协方差应尽可能小;
- 然后,异类样例的投影点尽可能远离意味着让类中心之间的距离应尽可能大,即 ∣ ∣ ω T μ 0 − ω T μ 1 ∣ ∣ 2 2 ||\omega^T\mu_0-\omega^T\mu_1||_2^2 ∣∣ωTμ0−ωTμ1∣∣22尽可能大。
- 合起来,就等价于最大化:
J = ∣ ∣ ω T μ 0 − ω T μ 1 ∣ ∣ 2 2 ω T ∑ 0 ω + ω T ∑ 1 ω = ω T ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T ω ω T ( ∑ 0 + ∑ 1 ) ω J=\frac{||\omega^T\mu_0-\omega^T\mu_1||_2^2}{\omega^T\sum_0\omega+\omega^T\sum_1\omega}\\=\frac{\omega^T(\mu_0-\mu_1)(\mu_0-\mu_1)^T\omega}{\omega^T(\sum_0+\sum_1)\omega} J=ωT∑0ω+ωT∑1ω∣∣ωTμ0−ωTμ1∣∣22=ωT(∑0+∑1)ωωT(μ0−μ1)(μ0−μ1)Tω
定义类内散度矩阵(within-class scatter matrix):
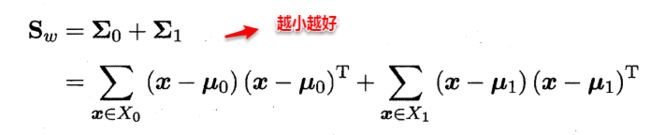
定义类间散度矩阵(between-class scatter matrix):
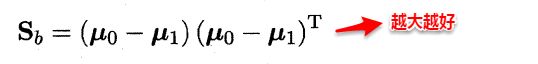
这两个矩阵的规模都是 d×dd\times dd×d,其中 ddd 是样例的维度(属性数目)。于是可以重写目标函数为:
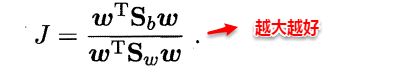
这就是LDA欲最大化的目标,即 S b S_b Sb和 S ω S_\omega Sω的“广义瑞利商”
可以注意到,分子和分母中 ω \omega ω都是二次项,因此,最优解与 ω \omega ω 的大小无关,只与方向有关。令分母为1,用拉格朗日乘子法把约束转换为方程,再稍加变换我们便可以得出:
ω = S ω − 1 ( μ 0 − μ 1 ) \omega=S_\omega^{-1}(\mu_0-\mu_1) ω=Sω−1(μ0−μ1)
但一般不直接对矩阵 S ω S_\omega Sω求逆,而是采用奇异值分解的方式。
从而分类问题转化为最优化求解 ω \omega ω的问题,当求解出 ω \omega ω后,对新的样本进行分类时,只需将该样本点投影到这条直线上,根据与各个类别的中心值进行比较,从而判定出新样本与哪个类别距离最近。
参考资料:
西瓜书
吴恩达机器学习课程
python机器学习基础教程。
南瓜书
未完待续





