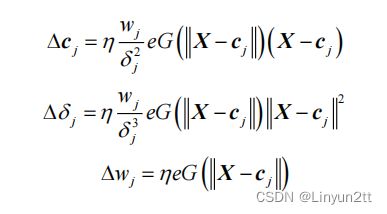神经网络——Python实现RBF 网络模型的实际应用

 来源：小凌のBlog—Good Times|一个不咋地的博客

一、正则化RBF 

用RBF网络解决插值问题时，基于上述正则化理论的 RBF网络称为正则化网络。其特点是隐节点数等于输人样本数，隐节点的激活函数为Green函数，常具有式a（r）=exp（-r的平方/2*σ的平方）的Gauss形式，并将所有输入样本设为径向基函数的中心，各径向基函数取统一的扩展常数。
由于正则化网络的训练样本与“基函数”是一一对应的。当样本数 P 很大时，实现网络的计算量将大得惊人，此外 P 很大则权值矩阵也很大，求解网络的权值时容易产生病态问题。为解决这一问题，可减少隐节点的个数，即 N < M < P，N 为样本维数，P 为样本个数，从而得到广义 RBF 网络。

图片来源于网络

 

广义 RBF 网络的基本思想是：用径向基函数作为隐单元的“基”，构成隐含层空间。隐含层对输入向量进行变换，将低维空间的模式变换到高维空间内，使得在低维空间内的线性不可分问题在高维空间内线性可分。RBF 网络的学习算法（数据中心的监督学习算法）采用梯度下降算法，以忽略阈值的单输出网络为例，单样本训练的参数更新公式如下：

图片来源于网络

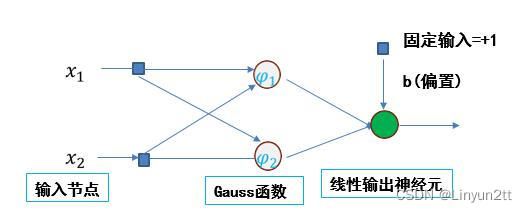
二、简要图 

 

图片来源于网络

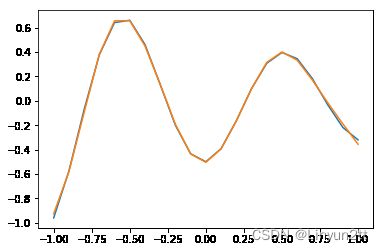
三、运行结果 

这里为了运用算法，简要的举了一个例子，仅供参考
输入 ：
X=-1:0.1:1

输出 ：
D=[-0.96 -0.577 -0.0729 0.377 0.641 0.66 0.461 0.1336 -0.201 -0.434 -0.5 -0.393 -0.1647 0.0988 0.3072 0.396 0.3449 0.1816 -0.0312 -0.2183 -0.3201]
详细代码查看最底部

 

########################误差 1.97094######################第0次迭代
########################误差 0.87572######################第100次迭代
########################误差 0.58298######################第200次迭代
########################误差 0.29211######################第300次迭代
########################误差 0.08972######################第400次迭代
########################误差 0.04544######################第500次迭代
########################误差 0.02676######################第600次迭代
########################误差 0.01461######################第700次迭代
########################误差 0.00708######################第800次迭代
########################误差 0.00354######################第900次迭代
[-1.] -> [[-0.92630567]]
[-0.9] -> [[-0.5819172]]
[-0.8] -> [[-0.09586922]]
[-0.7] -> [[0.38054865]]
[-0.6] -> [[0.65524628]]
[-0.5] -> [[0.65606183]]
[-0.4] -> [[0.44954136]]
[-0.3] -> [[0.13573688]]
[-0.2] -> [[-0.19378414]]
[-0.1] -> [[-0.4351655]]
[-2.22044605e-16] -> [[-0.50417201]]
[0.1] -> [[-0.39375574]]
[0.2] -> [[-0.16560002]]
[0.3] -> [[0.09903841]]
[0.4] -> [[0.31451208]]
[0.5] -> [[0.40014661]]
[0.6] -> [[0.33274067]]
[0.7] -> [[0.16960969]]
[0.8] -> [[-0.01452695]]
[0.9] -> [[-0.18870826]]
[1.] -> [[-0.35617567]]
>>>S
[[-2.06216068e+01]
 [-6.23379026e-01]
 [-2.75235180e-01]
 [-1.83220403e-01]
 [-3.51571592e-01]
 [-3.74599402e-01]
 [-6.51551503e-01]
 [-3.80983180e-01]
 [ 2.21513900e-01]
 [ 7.83684980e-03]
 [-1.76384505e-01]]
>>>C
[[-2.02833963  0.76382975 -0.3515109  -0.65582968 -0.16646301  0.71497565
   0.16555357  0.66236107 -0.09091257 -0.94265449  0.48418609]]
>>>权值
[[ 1.27165879]
 [ 0.26187551]
 [ 0.85204661]
 [ 0.8898032 ]
 [ 0.69645458]
 [ 0.30058268]
 [ 0.46231703]
 [ 0.34839319]
 [-1.02111873]
 [ 0.1330878 ]
 [ 0.36195479]]

四、rbf算法程序

# -*- coding: utf-8 -*-
import math
import string
import matplotlib as mpl
############################################调用库（根据自己编程情况修改）
import numpy.matlib 
import numpy as np
np.seterr(divide='ignore',invalid='ignore')
import matplotlib.pyplot as plt
from matplotlib import font_manager
import pandas as pd
import random

#生成区间[a,b]内的随机数
def random_number(a,b):
    return (b-a)*random.random()+a
 
#生成一个矩阵，大小为m*n,并且设置默认零矩阵
def makematrix(m, n, fill=0.0):
    a = []
    for i in range(m):
        a.append([fill]*n)
    return np.array(a)
#求取范数
def metrics(a): 
    return np.linalg.norm(a, axis=1, keepdims=True)


#构造三层BP网络架构
class BPNN:
    def __init__(self, num_in, num_hidden, num_out, num_p):
        #输入层，隐藏层，输出层的节点数
        self.num_in = num_in
        self.num_hidden = num_hidden + 1   #增加一个偏置结点
        self.num_out = num_out
        self.num_p = num_p
        #激活神经网络的所有节点（向量）
        self.active_in = np.array([-1.0]*self.num_in)
        self.active_hidden = np.array([-1.0]*self.num_hidden)
        self.active_out = np.array([1.0]*self.num_out)

        #创建初始化变量
        self.x_c=makematrix(self.num_p,self.num_hidden)
        self.G = makematrix(self.num_p,self.num_hidden)
        self.ei = makematrix(self.num_p,1)#所有样本误差信号
        self.i=0
        
        #创建权重矩阵以及其他变量
        self.C=makematrix(self.num_in,self.active_hidden)
        self.S=makematrix(self.num_hidden,1)
        self.wight_out = makematrix(self.num_hidden, self.num_out)
        
        #初始化权值以及其他变量
        for i in range(self.num_in):
            for j in range(self.num_hidden):
                self.C[i][j]=random_number(-1, 1)
        for i in range(self.num_hidden):
            for j in range(self.num_out):
                self.wight_out[i][j] = random_number(0.01, 0.2)
            self.S[i]=random_number(-1, 1)
        #初始化偏差
        for j in range(self.num_out):
            self.wight_out[0][j] = 0.5
  


    #基函数（高斯函数）sigmoid_hidden()
    def sigmoid_hidden(self,x):
        r=metrics(x-self.C.T)**2
        return np.exp(-1*r/(2*self.S**2))

    #函数sigmoid_out()
    def sigmoid_out(self,x):
        return np.dot(x.T,self.wight_out)

    #信号正向传播
    def update(self, inputs):
        if len(inputs) != self.num_in:
            raise ValueError('与输入层节点数不符')
            
        #数据输入输入层
        self.active_in=inputs
        #数据在隐藏层的处理
        self.active_hidden=self.sigmoid_hidden(self.active_in)   #active_hidden[]是处理完输入数据之后存储，作为输出层的输入数据
        self.active_hidden[0]=-1
        #数据在输出层的处理
        self.active_out = self.sigmoid_out(self.active_hidden)   #与上同理
        #print(self.active_out)
        return self.active_out

    def error_ei(self,targets,inputs):
         #误差
        if self.i==self.num_p:
            self.i=0
        self.ei[self.i]=targets-self.update(inputs)
        self.x_c[self.i]=inputs-self.C
        self.G[self.i]=self.active_hidden.T
        self.i=self.i+1
        
    #反向传播
    def errorbackpropagate(self,lr):   #lr是学习率
        self.error=(1/2)*(np.dot(makematrix(1,self.num_p,1),self.ei**2)) 
        self.C=self.C+lr*((self.wight_out/(self.S**2)).T)*np.dot(self.ei.T,self.G*self.x_c)
        self.S=self.S+lr*(self.wight_out/(self.S**3))*(np.dot(self.ei.T,self.G*(self.x_c)**2).T)
        self.wight_out=self.wight_out+lr*np.dot(self.ei.T,self.G).T 
        return self.error

    #测试
    def test(self, patterns):
        t=np.array([0.0]*21)
        a=0
        for i in patterns:
            print(i[0:self.num_in], '->', self.update(i[0:self.num_in]))
            t[a]=self.update(i[0:self.num_in])
            a+=1
        return t

    #权重
    def weights(self):
        print(">>>S")
        print(self.S)
        print(">>>C")
        print(self.C)
        print(">>>权值")
        print(self.wight_out)
    #训练
    def train(self, pattern, itera=1000, lr = 0.01):#训练1000次，学习率为0.01
        for i in range(itera):
            for j in pattern:
                inputs = j[0:self.num_in]
                targets = j[self.num_in]
                self.error_ei(targets,inputs)
            error = self.errorbackpropagate(lr)
            #print("!!!!!!!!!",(self.G*self.x_c))
            if i % 100 == 0:
                print('########################误差 %-.5f######################第%d次迭代' %(error,i))

#实例
X=np.arange(-1,1.1,0.1)
D=[-0.96, -0.577, -0.0729, 0.377, 0.641, 0.66, 0.461, 0.1336, -0.201, -0.434, -0.5, -0.393, -0.1647, 0.0988, 0.3072, 0.396, 0.3449, 0.1816, -0.0312, -0.2183, -0.3201]
patt=np.array(list(zip(X,D)))
#print(patt)
    #创建神经网络，1个输入节点，10个隐藏层节点，1个输出层节点,21个样本
n = BPNN(1, 10, 1, 21)
    #训练神经网络
n.train(patt)
    #测试神经网络
patt2=n.test(patt)
    #查阅权重值
n.weights() 
    #绘制图形
plt.plot(X,D)
plt.plot(X,patt2)
plt.show()

---

来源：小凌のBlog—Good Times|一个不咋地的博客https://blog.ling08.cn/index.php/post-232.html
[1]   韩力群，人工神经网络理论及应用 [M]. 北京：机械工业出版社，2016.