【论文翻译】VectorNet: Encoding HD Maps and Agent Dynamics from Vectorized Representation

VectorNet: 通过向量化表示编码高精度地图与动态交通参与者

摘要： 由于动态交通参与者（如行人和车辆等）和静态道路环境（如车道，交通灯等）的复杂表示以及之间的交互关系，在动态的，多交通参与者的场景下的行为预测是自动驾驶领域的一个重要问题。这篇文章提出了一个分层的图神经网络VectorNet，首先分别用向量表示不同局部空间的道路组成成员（包括动态交通参与者和静态道路环境），然后对所有的成员之间的高阶交互关系进行建模。与将动态交通参与者的运动轨迹和道路环境信息直接渲染在鸟瞰图像上并通过卷积神经网络对其进行编码的方法不同，我们的方法直接在矢量化的高精度地图上操作，避免了渲染损失以及计算密集的卷积神经网络编码步骤。为了进一步激发VectorNet学习特征的能力，我们提出一个通过其他道路组成成员特征还原随机掩盖的成员特征的新的辅助任务。我们在最近开源的Argoverse预测数据集和我们内部的行为预测数据集上评估了VectorNet的性能。在两个数据集上，我们的方法都达到了与采用渲染鸟瞰图像实现预测的方法相当甚至更好的性能，同时减少了超过70%的模型参数以及一个数量级的运算量。VectorNet在Argoverse数据集上的预测性能优于目前的最好水平。

1. 前言

这篇文章聚焦于复杂的，多交通参与者的场景下的行为预测。研究的核心在于找到整合通过感知系统获得的动态交通参与者和以高精度地图的形式给出的场景信息的统一表示。我们的目标是搭建一个系统学习去预测车辆的意图，并以运动轨迹的形式表示。

传统的行为预测方法是规则的，基于道路结构的约束生成多个行为假设。最近，很多基于学习的预测方法被提出[5,6,10,15]。他们提出了对于不同行为假设的进行概率解释的好处，但是需要重构一个新的表示来编码地图和轨迹信息。有趣的是，虽然高精度地图是高度结构化的，但是目前大多数预测方法选择将高精度地图渲染成颜色编码的属性（如图1的左图所示），并且采用感受野有限的卷积神经网络对场景信息进行编码。这就带来了一个疑问：我们能否直接从结构化的高精度地图中学习到有意义的场景信息表示？

我们提出直接从它们的矢量形式中学习一个动态交通参与者和结构化场景的统一的表示（如图1的右图所示）。道路特征的地理延伸可以是一个点，多边形或是曲线。例如，车道边界包含可以构成样条曲线的多个控制点；人行横道是由几个点定义的多边形；停止标识通过一个点来表示。所有的地理实体都可以被近似为多个控制点定义的折线。同时，动态交通参与者也可以通过他们的运动轨迹被近似为折线。所有的这些折线都可以表示为矢量的集合。

图1. 栅格化渲染方法（左）和矢量化方法（右）表示高精度地图与交通参与者运动轨迹

我们使用图神经网络来合并这些向量的集合。我们将每个向量视为图中的一个节点，并且定义节点的特征包含每个向量的起始位置和结束位置，以及其它属性，包括折线ID和语义标签。通过图神经网络，高精度地图的环境信息和其他交通参与者的运动轨迹被整合到目标交通参与者节点上。然后我们可以解码目标交通参与者输出的节点特征来预测它未来的运动轨迹。

特别地，为了学习图神经网络的竞争性表示，我们发现基于节点的空间和语义邻近性来约束图的连通性是很重要的。因此，我们提出了一个分层的图网络结构，首先把具有相同折线ID，并且具有相同语义标签的向量整合成折线特征，然后所有不同的折线特征互相连通交换信息。我们通过多层感知机实现局部图，通过自注意力机制[30]实现全局图。我们的方法如图2所示。

图2. 我们提出的VectorNet框架。观察到的交通参与者运动轨迹和地图特征被表示为矢量序列，然后传入局部图网络中获得折线级的特征。这些特征然后被传入一个全连接图网络中来建模高阶的交互。我们计算两类损失：从目标交通参与者对应的节点特征中预测其未来轨迹，以及预测图网络中被掩盖的节点特征。

最后，受到来自连续语音[11]和视觉数据[27]中采用自监督学习方法的有效性的启发，在行为预测目标之外我们提出一个辅助的图像补全目标。具体来说就是，我们随机掩盖属于静态场景或是动态轨迹的节点特征，然后让模型重构被掩盖的特征。我们直觉上认为这样可以鼓励图网络结构更好地捕捉动态交通参与者和静态环境之间的交互。总而言之，我们的贡献主要是：

• 我们是最先证明如何直接整合矢量化的场景信息和动态交通参与者信息来实现行为预测。

• 我们提出了双层图网络结构VectorNet和节点补全辅助任务。

• 我们在我们内部的行为预测数据集和Argoverse数据集上评估了提出的方法，结果表明我们的方法在减少了超过70%的模型参数以及一个数量级的运算量的情况下达到了与采用渲染鸟瞰图实现预测的方法相当甚至更好的性能。同时，我们的方法在Argoverse数据集上达到了目前最优的水平。

2. 相关工作

自动驾驶中的行为预测。在自动驾驶领域中，对动态的交通参与者的行为预测变得越来越重要[7,9,19]，并且高精度地图也被广泛应用来提供环境信息。例如，IntentNet[5]通过LiDAR点云和渲染的高精度地图进行车辆检测并预测它们的运动轨迹。[15]假设已经得到车辆的检测结果并聚焦于通过卷积神经网络编码交互关系来实现行为预测。MultiPath[6]也采用卷积神经网络作为编码器并通过预先定义的候选轨迹来回归多个可能的未来轨迹。PRECOG[23]尝试通过基于流的生成模型捕捉未来的随机性。与[6,15,23]相似，我们也假设已经通过感知模块得到了检测结果。但是，不像那些采用卷积神经网络来编码渲染的道路地图的方法，我们提出直接编码矢量化的场景信息和动态交通参与者。

预测多个交通参与者之间的交互。在自动驾驶领域之外，更普遍的兴趣是预测交互对象之间的意图。例如对行人[2,13,24]，人类活动[28]或是对体育运动员[12,26,32,33]。Social LSTM[2]采用单独的LSTM网络建模不同交通参与者的运动轨迹，并且聚合空间邻近的交通参与者的LSTM隐藏层来建模他们之间的交互关系。Social GAN[13]简化了交互建模并且提出采用生成对抗网络来预测多条可能的未来轨迹。[26]结合图神经网络[4]和变分循环神经网络[8]来建模交互关系。社会交互关系也可以从数据中推理出来，[18]将这些交互关系视为潜在变量。图注意网络[16,31]应用自注意力机制来给预定义的图中的边赋予权重。我们更进一步地提出了一个统一的分层的图网络结构来同时建模多个交通参与者之间的交互关系，以及他们和道路环境之间的交互关系。

自监督场景建模。最近，在自然语言处理领域的很多工作提出了自监督建模方法[11,22]。当学习成果被转移到下游任务时，取得了显著的效果提升。受到这些方法的启发，我们提出了一个图表示的辅助损失，它通过其他节点的特征来预测缺失的节点特征。其目标是激励模型更好地捕捉节点之间的交互。

3. VectorNet方法

这个部分介绍了我们提出的VectorNet方法。我们首先介绍如何矢量化动态交通参与者的轨迹和高精度地图。接下来我们提出了层级网络，它先分别聚合来自不同折线的局部特征，然后在全局上整合所有轨迹和地图特征。这个图最后将用于行为预测。

3.1. 表示轨迹和地图

大多数高精度地图的标注是以样条曲线（如车道线）、封闭形状（如交叉路口）和点（如红绿灯）的形式呈现，并且附带属性信息，如语义标签和当前状态（如交通灯的颜色，道路的速度限制）。对于动态交通参与者，他们的轨迹是关于时间的有向样条曲线的形式。所有这些元素元素都可以近似为矢量序列：对于地图特征，我们选择一个起点和方向，均匀地以相同的空间距离在样条曲线上采样关键点，然后把相邻的关键点串联成向量；对于轨迹，我们可以通过固定的时间间隔（0.1秒）采样关键点，并将它们连接成向量。如果给定的时空间隔足够小，得到的这些折线就与原始地图和轨迹十分接近。

我们向量化的过程是一个在连续轨迹，地图标注和矢量集合之间的一对一的映射，虽然后者是无序的。这使我们可以在矢量集合上构建一个可以被图神经网络编码的图表示结构。更具体地说，我们将属于折线$P_j$的每一个向量$v_i$看出图中的一个节点，节点特征如下：
$$V_i=[d_i^s,d_i^e,a_i,j],\text{\hspace{1em}(1)}$$
其中$d_i^s$和$d_i^e$是向量的起点和终点坐标，其可以表示为2D坐标$(x,y)$或是3D坐标$(x,y,z)$；$a_i$对应属性特征，比如动态交通参与者的类型，轨迹的时间戳，或是道路特征的类型，或是车道线的速度限制。$j$是$P_j$的id，表示$v_i$属于$P_j$。

为了使输入的节点特征与对应的交通参与者的位置无关，我们将所有矢量的坐标原点确定在对应的交通参与者最后被观察到的位置。一个将来的工作是为所有交互的交通参与者设定一个坐标原点，这样他们的轨迹可以被平行地预测出来。

3.2. 构建折线子图

为了利用节点的局部空间和语义信息，我们采用了层级的方法，首先在向量层级上构建子图，其中属于同一折线的所有向量节点互相连接。假设一个折线$P$包含节点$\{V_1,V_2,\dots ,V_P\}$，我们定义一层子图的前向操作如下：
$$V_i^{(l+1)}={\varphi }_{rel}(g_{enc}(V_i^{(l)}),{\varphi }_{agg}(\{g_{enc}(V_j^{(j)})\})),\text{\hspace{1em}(2)}$$

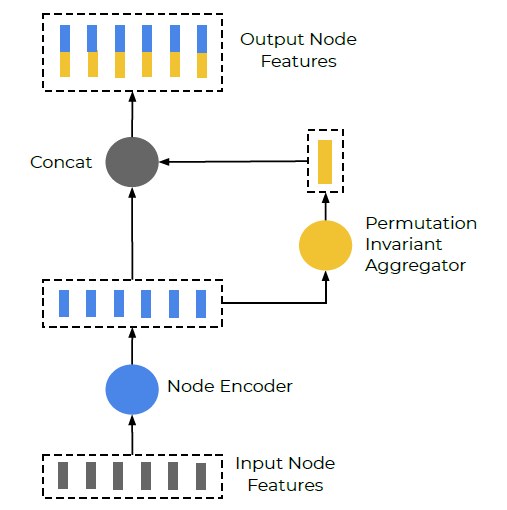
图3. 同一折线的向量节点的计算流

其中$V_i^{(l)}$是子图网络第$l$层的节点特征，$V_i^{(0)}$是输入特征$V_i$。函数$g_{enc}(\cdot )$编码独立的节点特征，${\varphi }_{agg}(\cdot )$聚合所有相邻节点的特征，${\varphi }_{rel}(\cdot )$是节点$V_i$与其相邻节点之间的关系运算。

实际上，$g_{enc}(\cdot )$是一个在所有节点中共享权重的多层感知器（MLP）。具体来说，MLP包含一个的全连接层，然后是层归一化[3]，最后是ReLU激活函数。${\varphi }_{agg}(\cdot )$是一个最大池化操作，${\varphi }_{rel}(\cdot )$是一个简单的拼接。如图3所示。我们堆叠多层子图网络，其中每层$g_{enc}(\cdot )$的权重是不一样的。最后，为了获取折线的特征，我们计算：
$$P={\varphi }_{agg}(\{V_i^{(L_p)}\}),\text{\hspace{1em}(3)}$$
其中${\varphi }_{agg}(\cdot )$仍是最大池化。

我们的折线子图网络可以被认为是PointNet[22]的推广：当我们令$d_s=d_e$，并且使$a$和$l$为空，我们的网络和PointNet具有相同的输入和计算流。但是，通过将排序信息嵌入到向量中，基于不同的折线ID可以限制子图的连通性，同时将属性编码到节点特征中，我们的方法尤其适合编码结构化的地图标注和交通参与者的运动轨迹。

3.3. 用于高阶交互的全局图

我们现在考虑通过一个全局交互图来建模折线节点特征$\{P_1,P_2,\dots .,P_P\}$上的高阶交互：
$$\{P_i^{(l+1)}\}=GNN(\{P_i^{(l)}\},A)\text{\hspace{1em}(4)}$$

其中，$\{p_i^{(l)}\}$是折线节点特征的集合，$GNN(\cdot )$为一层图神经网络，$A$为折线节点集合的邻接矩阵。

领接矩阵$A$可以是启发式的，例如使用节点之间的空间距离[2]。为简单起见，我们假设$A$是一个全连接图。我们的图网络通过自注意力机制实现[30]:
$$GNN(P)=softmax(P_Q{P}_K^T)P_V\text{\hspace{1em}(5)}$$
其中$P$是节点的特征矩阵，$P_Q$，$P_K$和$P_V$是它的线性映射。

然后我们从动态交通参与者对应的节点解码预测的未来轨迹：
$$V_i^{future}={\varphi }_{traj}(P_i^{(L_t)})\text{\hspace{1em}(6)}$$

其中$L_t$是$GNN$的层数，${\varphi }_{traj}(\cdot )$是轨迹解码器。为了简单起见，我们使用一个MLP作为轨迹解码器。更多高级的解码器，比如MultiPath[6]提出的基于候选轨迹的方法，或是变分循环神经网络[8,26]都可以用来生成多样化的轨迹；这些解码器是我们输入编码器的补充。

我们在实现中使用单个$GNN$层，这样在测试期间，只需要计算目标交通参与者所对应的节点特征。但是如果需要，我们也可以堆叠多层$GNN(\cdot )$来建模高阶交互。

为了鼓励我们的全局交互图更好地捕捉不同轨迹和地图之间的交互，我们提出了一个辅助的图补全任务。在训练过程中，我们随机掩盖一些折线节点的子集特征，如$P_i$，然后尝试去还原被掩盖的节点特征：
$$\widehat{P_i}={\varphi }_{node}(P_i^{(L_t)})\text{\hspace{1em}(7)}$$

其中${\varphi }_{node}(\cdot )$是通过MLP实现的节点特征解码器。这些节点特征解码器在推理阶段是不会使用的。

回顾一下，$P_i$是一个全连接的，无序的图中的一个节点。为了能够识别出对应的节点当它对应的节点特征被掩盖时，我们计算出所有属于对应节点$P_i^{id}$的向量中的起始点坐标的最小值。然后定义输入节点的特征为：
$$P_i^{(0)}=[P_i;P_i^{(id)}]\text{\hspace{1em}(8)}$$

我们的图补全任务和自然语言处理中获得巨大成功的BERT[11]方法息息相关，它从文本数据的上下文线索中预测缺失的文本输入。我们将这个训练目标推广到处理无向图中。不像最近一些方法（如[25]），将BERT推广到具有预计算的视觉特征的无序图像块，我们的节点特征是在端到端的框架中共同优化的。

3.4.整体框架

建立层级图神经网络后，我们对多任务训练目标进行优化：
$$L=L_{traj}+\alpha L_{node}\text{\hspace{1em}(9)}$$

其中$L_{traj}$是对未来真值轨迹的负高斯对数似然，$L_{node}$是预测的节点特征和被掩盖的真值节点特征之间的Huber损失，$\alpha =1.0$是一个用来平衡两个损失项的标量。为了通过降低节点特征的大小来避免$L_{node}$的平凡解，我们在将折线节点特征输入到全局图网络之前对其进行$L2$归一化。

我们预测的轨迹参数化为每个时间步的坐标偏移，并从最后一个观测位置开始。同时，我们基于预测目标车辆最后一个观察时刻的朝向旋转坐标系。