数字图像处理之均值滤波

图像噪声，通常指图像中除了成像物体之外的其它信息，比如斑点和颗粒，这些额外的错误信息干扰了成像物体的显示，影响成像质量，所以往往需要通过图像滤波（也称为图像去噪）来消除这些噪点。常见的图像滤波算法有均值滤波、高斯滤波、中值滤波、双边滤波、非局部均值滤波，以及近几年火热的基于深度学习的图像滤波等。本章节将详细讲解均值滤波算法的原理，以及C++实现和优化。

首先膜拜一下那些写Opencv代码的大佬们，他们写的代码不仅稳定性良好，运行效率也超级高，很多时候我们费尽心思写了一个相同的算法，发现性能与Opencv的接口函数相比还是差了许多，所以会有一丢丢的心理落差，但是抱着学习的态度，追赶大佬的脚步，精益求精，相信我们自己也是可以的！

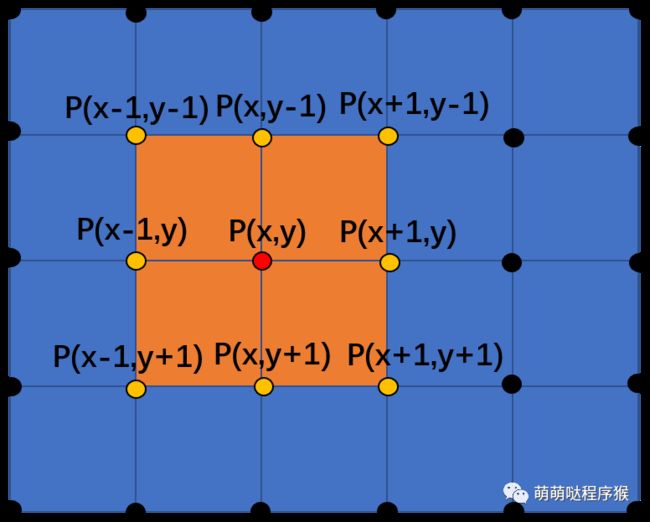
均值滤波，也就是计算每一个像素点周围像素点（包括该点）的平均值，作为该像素点滤波之后的值，通常取以该像素点为中心的矩形窗口内的所有像素点来计算平均值，矩形窗口的大小一般为3*3，5*5，9*9，...，(2n+1)*(2n+1)。窗口越大，滤波效果越好，但是图像也变得更加模糊，所以需要根据实际情况设置矩形窗口的大小。比如3*3窗口的均值滤波如下图所示，点(x,y)的滤波值由其周围9个点（包括其自身）计算平均值得到。

上图中点(x,y)的滤波值用公式表示为：

对于(2n+1)*(2n+1)窗口，点(x,y)的平均滤波值可根据如下公式计算：

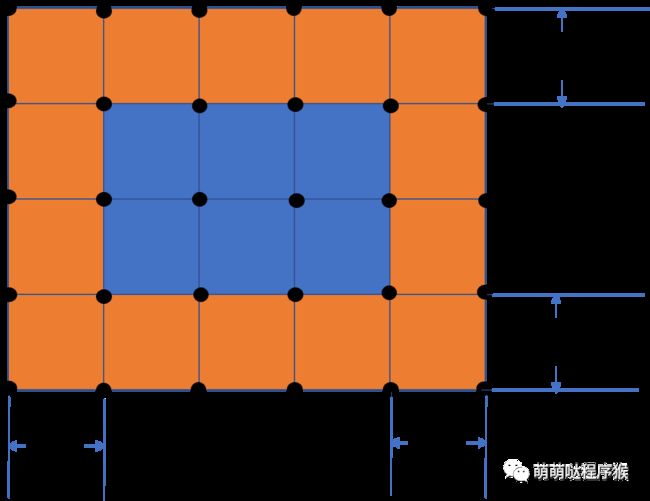
为了解决图像边缘像素点取不到完整矩形窗口的问题，通常先把图像的上、下边界扩充n行，左右边界扩充n列，实际计算时，只计算图像原有像素点的窗口平均值。比如当矩形窗口为3*3，则n的值为1，这种情况下扩充边界的示意图如下图所示：

根据以上原理，基于Opencv和C++的均值滤波实现代码如下：

void blur_mean(Mat src, Mat &dst, int winsize)
{
  if(winsize&1)   //如果窗口的边不是奇数，则加1使其为奇数，因为只有窗口的边为奇数的时候当前像素点才是窗口的中心点
  {
    winsize += 1;
  }
  const int winsize_2 = winsize/2;    //winsize_2 就是上述公式中的n
  const float winsize_num = winsize*winsize;   //(2n+1)*(2n+1)
  Mat src_board;
  //调用Opencv的copyMakeBorder函数扩充边界
  copyMakeBorder(src, src_board, winsize_2, winsize_2, winsize_2, winsize_2, BORDER_REFLECT);


  const int row = src_board.rows;   //行
  const int col = src_board.cols;
  Mat dst_tmp(src.size(), CV_8UC1);   //列
  for(int i = winsize_2; i < row-winsize_2; i++)  //行循环，只计算图像的原有行
  {
    for(int j = winsize_2; j < col-winsize_2; j++)  //列循环，只计算图像的原有列
    {
      float sum = 0.0;
      //计算每一个像素点周围矩形区域内所有像素点的累加和
      for(int y = 0; y < winsize; y++)
      {
        for(int x = 0; x < winsize; x++)
        {
          sum += src_board.ptr(i-winsize_2+y)[j-winsize_2+x];
        }
      }
      //求得累加和之后再求窗口像素的平均值。作为当前像素点的滤波值
      dst_tmp.ptr(i-winsize_2)[j-winsize_2] = (uchar)(sum/winsize_num + 0.5);
    }
  }
  dst_tmp.copyTo(dst);
}

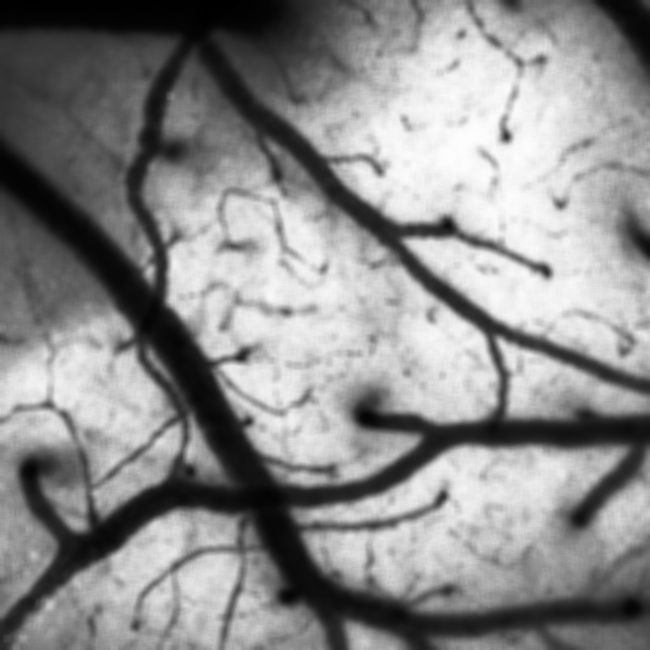
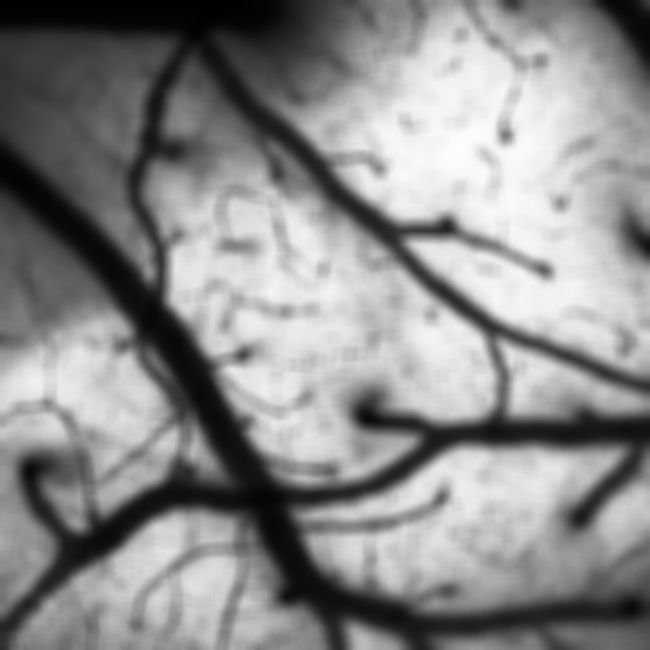
运行以上代码，对一帧1024*1024的图像进行均值滤波，得到的结果如下图所示。可以看到，随着窗口尺寸的增加，滤波图像变得更加模糊，整体耗时也大幅度增加，由此可以判断在滤波的计算过程中，主要耗时点为计算窗口内像素点的累加和。

 

原图  

3*3窗口，耗时17 ms

 

11*11窗口，耗时147.8 ms

21*21窗口，耗时535.4 ms

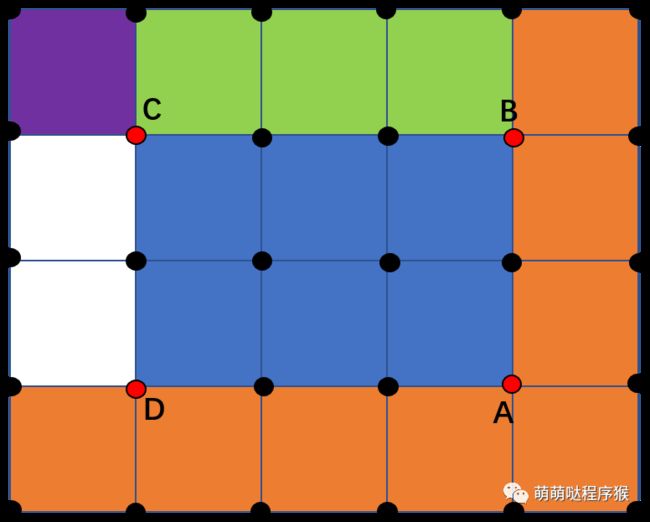
前面两篇文章中主要讲解了积分图的计算，根据积分图的特点，可以使用积分图来简化矩形窗口内像素累加和的计算，如下图所示，蓝色矩形区域内点的像素累加和，可以使用其四个顶点A、B、C、D的积分值来计算。

假设A、B、C、D的积分值分别为I(A)、I(B)、I(C)、I(D)，那么蓝色区域的像素累加和可以按照下式计算：

将上述积分图计算矩形区域内像素和的原理应用于均值滤波中，可以大大简化运算。对于每一个像素点，其计算滤波值的计算量由原本的(2n+1)*(2n+1)次加法，简化为2次加法和1次减法。

使用积分图优化加速的均值滤波代码如下：

void blur_mean_integral(Mat src, Mat &dst, int winsize)
{
  if(winsize&1)
  {
    winsize += 1;
  }


  const int winsize_2 = winsize/2;
  const float winsize_num = 1.0/(winsize*winsize);
  Mat src_board;
  copyMakeBorder(src, src_board, winsize_2, winsize_2, winsize_2, winsize_2, BORDER_REFLECT);


  Mat integral;
  Integal_row(src_board, integral);    //计算积分图


  const int row = src_board.rows;
  const int col = src_board.cols;
  dst.create(src.size(), CV_8UC1);


  for(int i = winsize_2; i < row-winsize_2; i++)
  {
    for(int j = winsize_2; j < col-winsize_2; j++)
    {
      //使用矩形区域四个顶点的积分值来计算区域内的x像素累加和
      float sum = integral.ptr(i+winsize_2)[j+winsize_2] - integral.ptr(i-winsize_2)[j+winsize_2] 
                - integral.ptr(i+winsize_2)[j-winsize_2] + integral.ptr(i-winsize_2)[j-winsize_2];
      //得到累加和之后再计算平均值
      dst.ptr(i-winsize_2)[j-winsize_2] = (uchar)(sum*winsize_num + 0.5);
    }
  }
}

运行以上代码，取窗口大小为21*21，同样对一帧1024*1024的图像进行均值滤波，耗时由535.4 ms减小到6.78 ms，可以看到，整体耗时大大减小。在使用积分图的基础上，再进行SSE指令的优化，可以进一步减小计算耗时：

void blur_mean_integral(Mat src, Mat &dst, int winsize)
{
  if(winsize&1)
  {
    winsize += 1;
  }


  const int winsize_2 = winsize/2;
  const float winsize_num = 1.0/(winsize*winsize);
  Mat src_board;
  copyMakeBorder(src, src_board, winsize_2, winsize_2, winsize_2, winsize_2, BORDER_REFLECT);


  Mat integral;
  Integal_row(src_board, integral);


  const int row = src_board.rows;
  const int col = src_board.cols;
  dst.create(src.size(), CV_8UC1);


  for(int i = winsize_2; i < row-winsize_2; i++)
  {
    float *p1 = integral.ptr(i-winsize_2);
    float *p2 = integral.ptr(i+winsize_2);
    uchar *p3 = dst.ptr(i-winsize_2);
    
    int j = winsize_2;
    for(; j < col-winsize_2-4; j+=4)   //列循环按4列展开，即每次循环同时计算4个点的滤波值
    {
      /*float sum = p2[j+winsize_2] - p1[j+winsize_2] - p2[j-winsize_2] + p1[j-winsize_2];
      p3[j-winsize_2] = (uchar)(sum*winsize_num + 0.5);
      sum = p2[j+winsize_2+1] - p1[j+winsize_2+1] - p2[j-winsize_2+1] + p1[j-winsize_2+1];
      p3[j-winsize_2+1] = (uchar)(sum*winsize_num + 0.5);
      sum = p2[j+winsize_2+2] - p1[j+winsize_2+2] - p2[j-winsize_2+2] + p1[j-winsize_2+2];
      p3[j-winsize_2+2] = (uchar)(sum*winsize_num + 0.5);
      sum = p2[j+winsize_2+3] - p1[j+winsize_2+3] - p2[j-winsize_2+3] + p1[j-winsize_2+3];
      p3[j-winsize_2+3] = (uchar)(sum*winsize_num + 0.5);*/
      
      //以下的SSE指令代码对应上方的C++代码
      __m128 a3, a2, a1, a0;
      //将4个点的同一方向顶点的像素值加载到__m128变量中
      //a3 : p2[j+winsize_2+3] p2[j+winsize_2+2] p2[j+winsize_2+1] p2[j+winsize_2]
      //a2 : p1[j+winsize_2+3] p1[j+winsize_2+2] p1[j+winsize_2+1] p1[j+winsize_2]
      //a1 : p2[j-winsize_2+3] p2[j-winsize_2+2] p2[j-winsize_2+1] p2[j-winsize_2]
      //a0 : p1[j-winsize_2+3] p1[j-winsize_2+2] p1[j-winsize_2+1] p1[j-winsize_2]
      a3 = _mm_loadu_ps(&p2[j+winsize_2]);
      a2 = _mm_loadu_ps(&p1[j+winsize_2]);
      a1 = _mm_loadu_ps(&p2[j-winsize_2]);
      a0 = _mm_loadu_ps(&p1[j-winsize_2]);
      
      //(a3-a2)+(a0-a1)
      __m128 sum = _mm_add_ps(_mm_sub_ps(a3, a2), _mm_sub_ps(a0, a1));
      __m128 winnum = _mm_set1_ps(winsize_num);  //winsize_num winsize_num winsize_num winsize_num


      sum = _mm_mul_ps(sum, winnum);  //sum中有4个浮点数，winnum中也有4个浮点数，两者对应位置的浮点数相乘
      __m128i sum_i = _mm_cvtps_epi32(sum);   //四舍五入取整


      p3[j-winsize_2+3] = (uchar)sum_i.m128i_i32[3];
      p3[j-winsize_2+2] = (uchar)sum_i.m128i_i32[2];
      p3[j-winsize_2+1] = (uchar)sum_i.m128i_i32[1];
      p3[j-winsize_2] = (uchar)sum_i.m128i_i32[0];
    }


    for(; j < col-winsize_2; j++)
    {
      float sum = p2[j+winsize_2] - p1[j+winsize_2] - p2[j-winsize_2] + p1[j-winsize_2];
      p3[j-winsize_2] = (uchar)(sum*winsize_num + 0.5);
    }
    
  }
}

使用SSE指令优化之后，同样对1024*1024的图像，取窗口21*21进行滤波，耗时由6.78 ms减少到3.98 ms。由此可知还是有一定优化效果的。