基于MVS的三维重建算法学习笔记(四)— 立体匹配经典算法Semi-Global Matching(SGM)论文翻译及要点解读
基于MVS的三维重建算法学习笔记(四)— 立体匹配经典算法Semi-Global Matching(SGM)论文翻译及要点解读
- 声明
- SGM概述
- Cost Calculation(像素代价计算)——MI互信息代价
- Aggregation of Costs(代价聚合)——光滑约束
- Disparity Computation(视差计算)——亚像素精度和遮挡检测
- Extension for Multi-Baseline Matching(多基线匹配扩展)
- 参考文献和资料
声明
本人书写本系列博客目的是为了记录我学习三维重建领域相关知识的过程和心得,不涉及任何商业意图,欢迎互相交流,批评指正。
SGM概述
精确、密集的立体匹配方法对于三维重建来说至关重要,其中所要面临的有三个问题——1.避免物体的精细结构边界模糊不清、2.对应像素强度由于光照和反射往往存在差异、3.计算效率需要提高;针对这三个问题,SGM提出了其解决方案,使得算法是精确的、鲁棒的、快速的。另一方面,目前的局部立体匹配算法采用支持窗口视差恒定(assume constant disparities within a correlation window)的假设,使得边界变得模糊;而全局立体匹配算法GC、BP等通过二维相邻像素视差之间的约束(如平滑性约束)而得到更好的匹配效果,但是速度较慢。
所以半全局立体匹配算法引入了互信息(MI,Mutual Information)代价来匹配对应强度关系复杂的图像,甚至可能是不同传感器的图像;并且提出了一种全局代价计算的近似用来提高效率,通过组合许多一维约束来逼近一个全局的、二维的光滑性约束。
Cost Calculation(像素代价计算)——MI互信息代价
匹配代价计算的是源图像像素 p \pmb{p} pp的强度intensity I b p I_{b\pmb{p}} Ibpp与目标匹配图像极线 q = e b m ( p , d ) \pmb{q}=e_{bm}(\pmb{p},d) qq=ebm(pp,d)上的所有待定的对应点 I m q I_{m\pmb{q}} Imqq。对于矫正后的图片而言, e b m ( p , d ) = [ p x − d , p y ] T e_{bm}(\pmb{p},d)=[\pmb{p}_x-d,\pmb{p}_y]^T ebm(pp,d)=[ppx−d,ppy]T,其中 d d d为视差。互信息是一种对图像明暗变化不敏感的相关性测度,通过两张图像各自的熵和两者之间的联合熵来定义: M I I 1 , I 2 = H I 1 + H I 2 − H I 1 , I 2 MI_{I_1,I_2}=H_{I_1}+H_{I_2}-H_{I_1,I_2} MII1,I2=HI1+HI2−HI1,I2其中对熵的理解参考了@王嗣钧:
熵是用来表征随机变量的不确定性(可以理解为变量的信息量),不确定性越强那么熵的值越大(最大为1),那么图像的熵其实就代表图像的信息量。互信息度量的是两个随机变量之间的相关性,相关性越大,那么互信息就越大。可以想想看,两幅图像如果匹配程度非常高,说明这两幅图像相关性大还是小?显然是大,知道一幅图像,另外一幅图像马上就知道了,相关性已经不能再大了!!!反之,如果两幅图像配准程度很低,那么两幅图像的互信息就会非常小。所以,立体匹配的目的当然就是互信息最大化。这就是为什么使用互信息的原因。
图像各自的熵和联合熵由图像强度的概率分布计算: H 1 = − ∫ 0 1 P l ( i ) l o g P l ( i ) d i H I 1 , I 2 = − ∫ 0 1 ∫ 0 1 P I 1 , I 2 ( i 1 , i 2 ) l o g P I 1 , I 2 ( i 1 , i 2 ) d i 1 d i 2 H_1=-\int^1_0P_l(i)logP_l(i)di \\ H_{I_1,I_2}=-\int^1_0\int^1_0P_{I_1,I_2}(i_1,i_2)logP_{I_1,I_2}(i_1,i_2)di_1di_2 H1=−∫01Pl(i)logPl(i)diHI1,I2=−∫01∫01PI1,I2(i1,i2)logPI1,I2(i1,i2)di1di2
对图像强度(intensity)的解释:对于一幅图像而言,最常见的强度表达就是图像像素的灰度值或者颜色信息,那么图像强度的概率分布函数 P l ( i ) P_l(i) Pl(i)是图像灰度直方图中灰度为i的点出现的概率,即每个灰度值对应的像素个数除以图像像素个数;同理 P I 1 , I 2 ( i 1 , i 2 ) = 1 n ∑ p T [ ( i 1 , i 2 ) = ( I 1 p , I 2 p ) ] P_{I_1,I_2}(i_1,i_2)=\frac{1}{n}\sum_{\pmb{p}}T[(i_1,i_2)=(I_{1p},I_{2p})] PI1,I2(i1,i2)=n1∑ppT[(i1,i2)=(I1p,I2p)]为两幅图像的联合概率密度——归一化后的统计直方图。
对于完全配准的图像,联合熵较低,互信息值较高。接着为了方便计算,也符合图像像素点离散化的特点,利用泰勒展开将联合熵 H I 1 , I 2 H_{I_1,I_2} HI1,I2转化为求和计算,每一项 h I 1 , I 2 h_{I_1,I_2} hI1,I2针对每个像素点 p \pmb{p} pp,并取决于相应的图像灰度值对 ( i , k ) (i,k) (i,k),下图展示了整个数据项 h I 1 , I 2 h_{I_1,I_2} hI1,I2加工的流程,其中 g ( i , k ) g(i,k) g(i,k)指的是高斯平滑处理, ⊗ \otimes ⊗为卷积运算: H I 1 , I 2 = ∑ p h I 1 , I 2 ( I 1 p , I 2 p ) h I 1 , I 2 ( i , k ) = − 1 n l o g ( P I 1 , I 2 ( i , k ) ⊗ g ( i , k ) ) ⊗ g ( i , k ) H_{I_1,I_2}=\sum_{\pmb{p}}h_{I_1,I_2}(I_{1p},I_{2p}) \\ h_{I_1,I_2}(i,k)=-\frac{1}{n}log(P_{I_1,I_2}(i,k)\otimes g(i,k))\otimes g(i,k) HI1,I2=pp∑hI1,I2(I1p,I2p)hI1,I2(i,k)=−n1log(PI1,I2(i,k)⊗g(i,k))⊗g(i,k)

一般情况下,图像各自的熵几乎是恒定的,图片匹配的结果取决于数据项 h I 1 , I 2 ( I 1 p , I 2 p ) h_{I_1,I_2}(I_{1p},I_{2p}) hI1,I2(I1p,I2p),然而如果考虑遮挡等一系列外部干扰, I 1 I_1 I1和 I 2 I_2 I2的强度会有一些不对应关系,这会导致非恒定的熵 H I 1 H_{I_1} HI1和 H I 2 H_{I_2} HI2,故在计算时也需要考虑: H I = ∑ p h I ( I p ) , h I ( i ) = − 1 n l o g ( P I ( i ) ⊗ g ( i ) ) ⊗ g ( i ) H_I=\sum_{\pmb{p}}h_I(I_{\pmb{p}}),h_I(i)=-\frac{1}{n}log(P_I(i)\otimes g(i))\otimes g(i) HI=pp∑hI(Ipp),hI(i)=−n1log(PI(i)⊗g(i))⊗g(i)这里还要注意,文章对于图像单独概率分布的计算没有取整个图像,而是只选择两幅图像的对应部分(否则将忽略遮挡, H I 1 H_{I_1} HI1和 H I 2 H_{I_2} HI2几乎为常数)并对联合概率函数对应部分的行和列进行求和得到 P I 1 ( i ) = ∑ k P I 1 , I 2 ( i , k ) P_{I_1}(i)=\sum_kP_{I_1,I_2}(i,k) PI1(i)=∑kPI1,I2(i,k);最后得到修改过的MI互信息定义,以及MI匹配代价的定义: M I I 1 , I 2 = ∑ p m i I 1 , I 2 ( I 1 p , I 2 p ) m i I 1 , I 2 ( i , k ) = h I 1 ( i ) + h I 2 ( k ) − h I 1 , I 2 ( i , k ) C M I ( p , d ) = − m i I b , f D ( I m ) ( I b p , I m q ) with q = e b m ( p , d ) MI_{I_1,I_2}=\sum_{\pmb{p}}mi_{I_1,I_2}(I_{1p},I_{2p}) \\ mi_{I_1,I_2}(i,k)=h_{I_1}(i)+h_{I_2}(k)-h_{I_1,I_2}(i,k) \\ C_{MI}(\pmb{p},d)=-mi_{I_b,fD(I_m)}(I_{b\pmb{p}},I_{m\pmb{q}})\text{ with }\pmb{q}=e_{bm}(\pmb{p},d) MII1,I2=pp∑miI1,I2(I1p,I2p)miI1,I2(i,k)=hI1(i)+hI2(k)−hI1,I2(i,k)CMI(pp,d)=−miIb,fD(Im)(Ibpp,Imqq) with qq=ebm(pp,d)
有关HMI分层互信息计算的部分解释参考了@王嗣钧:
作者采用分层互信息(HMI,hierarchical MI)进行代价匹配计算,由于概率分布图和图像大小无关(一直都是256x256),所以可以采用分层计算的方式来加速(反正不同层都是256x256),每一层的计算对应一次迭代,别忘记首次迭代需要基于视差图对右图进行warp,没有视差图怎么办?文章里面说是随机生成就好,并且由于像素个数很多,随机生成的个别错误可以被容忍,warp之后的右图和左图的匹配程度还是会比较高,迭代次数也相对较低,这也是SGM的一大优点;
作者还对HMI的时间复杂度进行了计算,由于单次迭代的时间复杂度是 O ( W H D ) O(WHD) O(WHD)(宽x长x视差),每次下采样都会令三个参数同时减半,所以上次迭代将会是当前迭代速度的1/8,假设我们有4次迭代,那么相比较于BT算法,只比它慢了14%,注意,算法首次迭代使用的是最小的视差图,并且乘以3的原因是随机生成的视差图十分不靠谱,需要反复迭代3次才能得到同样分辨率下的靠谱视差图,然后再参与后续高分辨率的计算。 1 + 1 2 3 + 1 4 3 + 1 8 3 + 3 1 1 6 3 ≈ 1.14 1+\frac{1}{2^3}+\frac{1}{4^3}+\frac{1}{8^3}+3\frac{1}{16^3}\approx1.14 1+231+431+831+31631≈1.14
Aggregation of Costs(代价聚合)——光滑约束
这里首先参考@李迎松~介绍一下全局能量最优化策略,即寻找每个像素的最优视差使得整张图像的全局能量函数最小:
全局能量函数的定义式为: E ( d ) = E d a t a ( d ) + E s m o o t h ( d ) E(d)=E_{data}(d)+E_{smooth}(d) E(d)=Edata(d)+Esmooth(d)其中 E d a t a E_{data} Edata为反应视差图总体匹配代价的测度; E s m o o t h E_{smooth} Esmooth是平滑约束,该约束会对相邻像素视差变化超过一定像素的情况进行惩罚(惩罚的概念就是加大能量值,阻碍优化进程)
解释下视差连续与视差非连续,视差连续代表局部范围内的像素的视差相差很小(1个像素内),是一个连续的变化趋势;而非连续是指局部范围内的像素视差相差很大(超过1个像素),是一个突变的变化趋势。这个局部范围往往是一个矩形的窗口(比如3x3、5x5)。由于视差和深度某种程度上其实是等价的,所以视差连续性背后表达的是空间中目标表面离相机的距离的连续性,如果是目标是连续的表面在影像上成像,则成像范围内视差也是连续的;而如果目标有前景和背景在影像上成像,则前景和背景的交界处,在局部窗口内会是一部分属于前景一部分属于背景,前景和背景离相机的距离就可能相差很大了,视差也会相差很大,即不连续。
SGM算法中的平滑约束与HMI代价计算合并构成了视差图 D D D上的能量函数 E ( D ) E(D) E(D): E ( D ) = ∑ p ( C ( p , D p ) + ∑ q ∈ N p P 1 T [ ∣ D p − D q ∣ = 1 ] + ∑ q ∈ N p P 2 T [ ∣ D p − D q ∣ > 1 ] ) E(D)=\sum_{\pmb{p}}(C(\pmb{p},D_{\pmb{p}})+\sum_{\pmb{q}\in N_{\pmb{p}}}P_1T[|D_{\pmb{p}}-D_{\pmb{q}}|=1]+\sum_{\pmb{q}\in N_{\pmb{p}}}P_2T[|D_{\pmb{p}}-D_{\pmb{q}}|>1]) E(D)=pp∑(C(pp,Dpp)+qq∈Npp∑P1T[∣Dpp−Dqq∣=1]+qq∈Npp∑P2T[∣Dpp−Dqq∣>1])第一项是视差图 D D D所有像素匹配代价的总和;第二项对 p \pmb{p} pp邻域 N p N_{\pmb{p}} Npp内的所有像素点 q \pmb{q} qq增加一个恒定的惩罚 P 1 P_1 P1,惩罚条件是若 p \pmb{p} pp和 q \pmb{q} qq的视差只差1像素;第三项对所有较大的视差变化增加了较大的常数惩罚 P 2 P_2 P2,惩罚条件是若 p \pmb{p} pp和 q \pmb{q} qq的视差大于1像素。
小变化低惩罚可以适应斜面和曲面,大变化高惩罚则可以保留图像的不连续性——由于影像的亮度边缘位置(也就是梯度较大的位置)是前景背景交界的可能性较大,这些位置的像素邻域内往往不是视差连续的,相差较大,为了保护真实场景中的视差非连续情况, P 2 P_2 P2往往是根据相邻像素的灰度差来动态调整的: P 2 = P 2 ′ I b p − I b q , P 2 > P 1 P_2=\frac{P_2'}{I_{b\pmb{p}}-I_{b\pmb{q}}}, P_2>P_1 P2=Ibpp−IbqqP2′,P2>P1, P 2 ′ P_2' P2′为 P 2 P_2 P2的初始值,一般设置为远大于 P 1 P_1 P1。
这个公式的含义是:如果像素和它的邻域像素亮度差很大,那么该像素很可能是位于视差非连续区域,则一定程度上允许其和邻域像素的视差差值超过1个像素,对于超过1个像素的惩罚力度就适当减小一点。
而接下来参考教程@王嗣钧,对于该能量函数的优化问题可以看做是一个动态规划的问题:
这个E对p是不可导的,这意味着我们常看到的梯度下降,牛顿高斯等等算法在这里都不适用,作者于是采用了动态规划来解决这一问题;简单地说,p的代价想要最小,那么前提必须是邻域内的点q的代价最小,q想要代价最小,那么必须保证q的领域点m的代价最小,如此传递下去。本文只说说作者是怎么利用动态规划来求解E,其实这个求解问题是NP完全问题,想在2D图像上直接利用动态规划求解是不可能的,只有沿着每一行或者每一列求解才能够满足多项式时间(又叫做扫描线优化),但是这里问题来了,如果我们只沿着每一行求解,那么行间的约束完全考虑不到,q是p的领域的点其实这个时候被弱化到了q是p的左侧点或者右侧点,这样的求优效果肯定很差。于是,大招来了!!我们索性不要只沿着横或者纵来进行优化,而是沿着一圈8个或者16个方向进行优化。
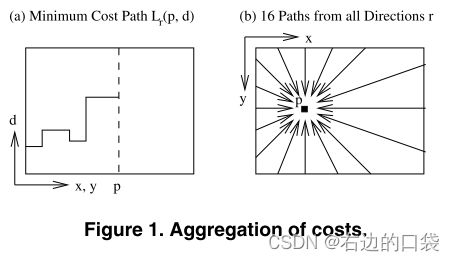
为了解决这一优化问题,SGM提出了一种从各个方向平均聚合一维匹配代价的新思想:对于像素 p \pmb{p} pp和视差 d d d的聚合(平滑)代价 S ( p , d ) S(\pmb{p},d) S(pp,d)是通过对所有一维最小代价路径求和得到的,其中这些路径是视差为 d d d的,以像素 p \pmb{p} pp为终点的路径。
令 L r ′ L'_{\pmb{r}} Lrr′为一条沿方向 r \pmb{r} rr穿过的路径,视差为 d d d的像素 p \pmb{p} pp的路径代价为 L r ′ ( p , d ) L'_{\pmb{r}}(\pmb{p},d) Lrr′(pp,d): L r ′ ( p , d ) = C ( p , d ) + m i n { L r ′ ( p − r , d ) L r ′ ( p − r , d − 1 ) + P 1 L r ′ ( p − r , d + 1 ) + P 1 m i n i L r ′ ( p − r , i ) + P 2 } − m i n k L r ′ ( p − r , k ) L'_{\pmb{r}}(\pmb{p},d)=C(\pmb{p},d)+min\left\{\begin{aligned} & L'_{\pmb{r}}(\pmb{p-r},d) \\& L'_{\pmb{r}}(\pmb{p-r},d-1)+P_1 \\& L'_{\pmb{r}}(\pmb{p-r},d+1)+P_1 \\ &min_iL'_{\pmb{r}}(\pmb{p-r},i)+P_2 \end{aligned}\right\}-min_k L'_{\pmb{r}}(\pmb{p-r},k) Lrr′(pp,d)=C(pp,d)+min⎩ ⎨ ⎧Lrr′(p−rp−r,d)Lrr′(p−rp−r,d−1)+P1Lrr′(p−rp−r,d+1)+P1miniLrr′(p−rp−r,i)+P2⎭ ⎬ ⎫−minkLrr′(p−rp−r,k)其中第一项为匹配代价值,属于数据项;第二项表示累加到路径代价上的值取不做惩罚、做 P 1 P_1 P1惩罚、做 P 2 P_2 P2惩罚三种情况中代价最小的值;第三项是为了保证新的路径代价值 L r L_{\pmb{r}} Lrr不超过一定的数值上限 L ≤ C m a x + P 2 L\leq C_{max}+P_2 L≤Cmax+P2,像素的总路径代价值 S ( p , d ) S(\pmb{p},d) S(pp,d)则通过 S ( p , d ) = ∑ r L r ( p , d ) S(\pmb{p},d)=\sum_{\pmb{r}}L_{\pmb{r}}(\pmb{p},d) S(pp,d)=∑rrLrr(pp,d)计算得到。
参考@李迎松~对于路径代价聚合的解释可以了解到:
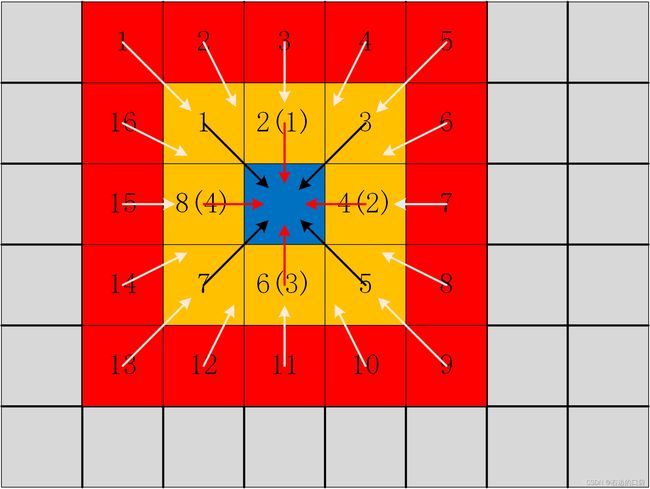
根据路径数不同,聚合的方向也有所不同,一般来说,有4路径(红色箭头方向)、8路径(红色+黑色箭头方向)和16路径(白色箭头方向)三种聚合方式,路径数越多效果越好,但是耗时也会越长,往往需要平衡利弊,根据应用的实际要求来选择合适的路径数。若取16路径的情况则可以得到 S ≤ 16 ( C m a x + P 2 ) S\leq 16(C_{max}+P_2) S≤16(Cmax+P2),这个不等式很重要,它表明选择合适的 P 2 P_2 P2值可以将聚合代价值 S S S控制在一定数值范围内,减少聚合代价数组对内存的占用。
SGM的代价聚合过程如下图所示:
Disparity Computation(视差计算)——亚像素精度和遮挡检测
在SGM算法中,视差计算采用赢家通吃(WTA)算法,每个像素选择最小聚合代价值所对应的视差值作为最终视差。
源图像 I b I_b Ib对应的视差图 D b D_b Db通过为每个像素 p \pmb{p} pp选择对应于最小成本的视差 d d d来确定,即 m i n d S ( p , d ) min_dS(\pmb{p},d) mindS(pp,d)。对于亚像素估计,通过邻近代价(即在下一个较高或较低视差处)拟合二次曲线,并计算最小值的位置。使用二次曲线在理论上只适用于使用差的平方和的简单相关。 但由于计算简单,采用IS作为近似。
通过遍历对应于匹配图像的像素 q \pmb{q} qq的极线,可以从相同的代价确定对应于匹配图像 I m I_m Im的视差图像 D m D_m Dm。同样,选择与最小代价相对应的视差值 d d d,即 m i n d S ( e m b ( q , d ) , d ) min_dS(e_{mb}(\pmb{q},d),d) mindS(emb(qq,d),d)。然而,代价聚合步骤不对称地处理源图像和匹配图像,因此,如果从零开始计算 D m D_m Dm,可以预期更好的结果。使用具有小窗口(即3×3)的中值滤波器从 D b D_b Db和 D m D_m Dm中过滤噪声点。
D b D_b Db和 D m D_m Dm的计算可以通过执行一致性检查来阻止识别遮挡和假匹配,将 D b D_b Db的每个视差与其对应的 D m D_m Dm视差进行比较,如果两者不同,则将差异设置为无效( D i n v D_{inv} Dinv)。 D p = { D b p i f ∣ D b p − D m q ∣ ≤ 1 , q = e b m ( p , D b p ) D i n v otherwise D_{\pmb{p}}=\left\{ \begin{aligned} & D_{b\pmb{p}} && if|D_{b\pmb{p}}-D_{m\pmb{q}}|\leq1,\pmb{q}=e_{bm}(\pmb{p},D_{b\pmb{p}}) \\ & D_{inv} && \text{otherwise} \end{aligned} \right. Dpp={DbppDinvif∣Dbpp−Dmqq∣≤1,qq=ebm(pp,Dbpp)otherwise
Extension for Multi-Baseline Matching(多基线匹配扩展)
参考文献和资料
[1]Stereo Matching文献笔记之(九):经典算法Semi-Global Matching(SGM)之神奇的HMI代价计算~
[2]【理论恒叨】【立体匹配系列】经典SGM:(1)匹配代价计算之互信息(MI)
[3]Semi-Global Matching(SGM)算法原文理解
[4]Visual Correspondence Using Energy Minimization and Mutual Information
[5]Accurate and Efficient Stereo Processing by Semi-Global Matching and Mutual Information
[6]Stereo Processing by Semi-Global Matching and Mutual Information
[7]Stereo Vision in Structured Environments by Consistent Semi-Global Matching