基于MVS的三维重建算法学习笔记(五)— 立体匹配经典算法PatchMatch论文翻译及要点解读
基于MVS的三维重建算法学习笔记(五)— 立体匹配经典算法PatchMatch论文翻译及要点解读
- 声明
- 问题提出
- 问题建模
- 通过PatchMatch获取平面参数——Inference via PatchMatch
-
- 1. 随机初始化(Random Initialization)
- 2. 迭代传播(Iteration)
-
- 2.1 空间传播(Spatial Propagation)
- 2.2 视图传播(View Propagation)
- 2.3 时序传播(Temporal Propagation)
- 2.4 平面优化(Plane Refinement)
- 总结
- 参考文献和资料
声明
本人书写本系列博客目的是为了记录我学习三维重建领域相关知识的过程和心得,不涉及任何商业意图,欢迎互相交流,批评指正。
问题提出
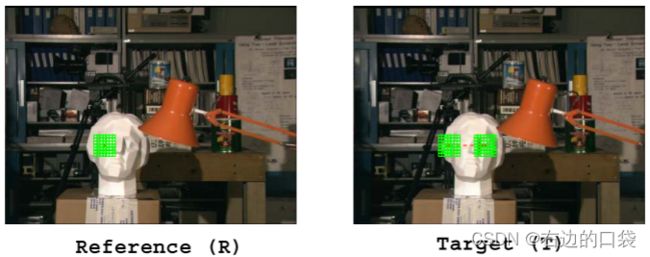
在局部立体匹配方法中,支持窗口(a support window)位于reference图像某一像素点的中间位置,并且在target图像中支持窗口会通过移动来找到颜色差异最小的点,作为该点的匹配对应点。在这个问题过程中,存在一个隐含的假设——即支持窗口内的所有像素都具有恒定的视差。但实际情况往往不是这样,一是支持窗口包含位于与中心像素不同的表面上的像素(也就是支持窗口中的像素可能在场景中处于不同表面),二是支持窗口有可能位于倾斜的表面。自适应支持权重方法(the adaptive support weight strategy)利用离散视差上的正面平行窗口(fronto-parallel windows at discrete disparities)很好地解决了问题一,重建的1维结果如下图(a)所示;但是可以看到,这种方法只能为点P找到最佳的支持窗口,因为点P的表面部分在全值视差1处与正面平行平面(the fronto-parallel plane)重合,很明显现实场景中很少能满足这样的情况。对于位于亚像素视差处的点Q、位于倾斜平面的点R以及位于球形平面的点S均无法用正面平行平面找到合适的支持窗口。

这样就引出了本文的策略,即在每一个像素点都计算一个单独的3D平面并且应用在待投影的支持区域。如上图(b)所示,这使得生成的支持窗口明显改善,能够完整的表示点P、Q、R所在的平面,而且对于S点处的平面,在实验中(如下图(c)所示)也显示具有较好的效果。在下图(a)具有高度倾斜以包含球形物体的走廊场景中,本文的方法(c)展现了比正面平行平面方法(b)更好的性能。

在本文中,作者提出了一种基于PatchMatch的算法,用以有效解决在每个像素处寻找一个好的倾斜支持平面(a good slanted support plane),与其他方法不同的是,该方法并不重建整个立体代价体——对于一个无限标签空间包含所有的3D平面是不可能的,而是巧妙地遍历其中一部分。PatchMatch是一种近似的稠密最近邻算法,即对于一个图像的每个patch计算第二个图像中相似颜色的patch的整数值向量(x,y)。并且使用随机搜索和传播的PatchMatch思想,在一个平面的极线上寻找最近邻点,这能够有效的处理倾斜表面和亚像素精度的问题。
问题建模
对于两幅图像的每个点对 p p p,搜寻一个平面 f p f_p fp,一旦 f p f_p fp被搜索到,就可以计算 p p p点的视差值 d p = a f p p x + b f p p y + c f p d_p=a_{f_p}p_x+b_{f_p}p_y+c_{f_p} dp=afppx+bfppy+cfp,其中 a f p a_{f_p} afp、 b f p b_{f_p} bfp和 c f p c_{f_p} cfp是平面 f p f_p fp的三个参数, p x p_x px和 p y p_y py是点p的横纵坐标。最后希望找到的平面 f p f_p fp应该是所有可能平面中聚合匹配代价(aggregated matching costs)最小的平面之一: f p = argmin f ∈ F m ( p , f ) f_p=\text{argmin}_{f\in \mathcal{F}}m(p, f) fp=argminf∈Fm(p,f),其中 F \mathcal{F} F代表大小为无限的所有平面的集合——但是这个无限的标签空间无法简单地检查所有可能的标签。平面 f f f的匹配像素 p p p的聚合代价为: m ( p , f ) = ∑ q ∈ W p w ( p , q ) ⋅ ρ ( q , q − ( a f p p x + b f p p y + c f p ) ) m(p,f)=\sum_{q\in W_p}w(p,q)·\rho(q,q-(a_{f_p}p_x+b_{f_p}p_y+c_{f_p})) m(p,f)=q∈Wp∑w(p,q)⋅ρ(q,q−(afppx+bfppy+cfp)),其中 W p W_p Wp表示以像素 p p p为中心的方形窗口,权重函数 w ( p , q ) w(p,q) w(p,q)用于克服边缘肥大问题(edge-fattening problem)并实现自适应支持权重思想。其通过查看像素的颜色来计算 p p p和 q q q位于同一平面上的可能性,即如果颜色相似,它会返回高值: w ( p , q ) = e − ∣ ∣ I p − I q ∣ ∣ γ w(p,q)=e^{-\frac{||I_p-I_q||}{\gamma}} w(p,q)=e−γ∣∣Ip−Iq∣∣。函数 ρ \rho ρ是在衡量两个像素的不相似性。假设左视图像素q的视差平面方程为 ( a f p , b f p , c f p ) (a_{f_p},b_{f_p},c_{f_p}) (afp,bfp,cfp)则它的视差值 d p = a f p p x + b f p p y + c f p d_p=a_{f_p}p_x+b_{f_p}p_y+c_{f_p} dp=afppx+bfppy+cfp,在右视图上的对应点 q ′ = q − d q q'=q-d_q q′=q−dq,则q和 q ′ q' q′的不相似性计算公式为: ρ ( q , q ′ ) = ( 1 − α ) ⋅ m i n ( ∣ ∣ I q − I q ′ ∣ ∣ , τ c o l ) + α ⋅ m i n ( ∣ ∣ Δ I q − Δ I q ′ ∣ ∣ , τ g r a d ) \rho(q,q')=(1-\alpha)·min(||I_q-I_{q'}||,\tau_{col})+\alpha·min(||\Delta I_q-\Delta I_{q'}||,\tau_{grad}) ρ(q,q′)=(1−α)⋅min(∣∣Iq−Iq′∣∣,τcol)+α⋅min(∣∣ΔIq−ΔIq′∣∣,τgrad)式中 ∣ ∣ Δ I q − Δ I q ′ ∣ ∣ ||\Delta I_q-\Delta I_{q'}|| ∣∣ΔIq−ΔIq′∣∣为q和 q ′ q' q′的梯度之差的绝对值,该式的含义就是两个像素的颜色相差越大、梯度相差越大,则不相似的程度越大; α \alpha α参数为自定义参数,在颜色和梯度之间做一个平衡。注意到根据平面算出来的视差值是小数值,所以像素 q ′ q' q′的位置不是整数而是小数,它的颜色值和梯度值通过线性内插得到。参数 τ c o l \tau_{col} τcol和 τ g r a d \tau_{grad} τgrad为自定义截断参数,为了让遮挡区的像素代价计算更鲁棒,意思就是不能让代价过大,保持在一个良好的局部范围内。
至此得到了一个完整定义的代价函数用来衡量一个平面表示的好坏,在匹配时应当选择代价最小的平面;但是由于空间中存在着无限个平面,所以不能简单的利用穷举的方法来搜寻,而是需要PatchMatch的思想来搜索。
通过PatchMatch获取平面参数——Inference via PatchMatch
PatchMatch的基本思想是:在自然图像中,一个有一定大小的像素块内所有像素都可以用同一个平面来近似。这也构成了PMS的基本思想,即图像可看作多个像素块,而每个像素块可有一个近似的视差平面,算法的目标就是要找到图像的所有视差平面。
1. 随机初始化(Random Initialization)
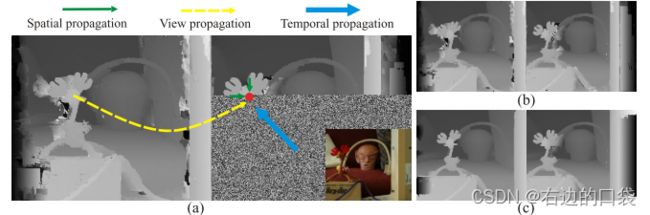
初始化的规则为:在给定的视差范围内每个像素随机生成一个视差值 z 0 z_0 z0,这样就得到了一个随机平面上的点 P = ( x 0 , y 0 , z 0 ) P=(x_0,y_0,z_0) P=(x0,y0,z0),紧接着生成一个随机的单位向量 n ⃗ = ( n x , n y , n z ) \vec{n}=(n_x,n_y,n_z) n=(nx,ny,nz)作为平面的法线,就可以得到平面的三个参数值: a f = − n x n z a_f=-\frac{n_x}{n_z} af=−nznx, b f = − n y n z b_f=-\frac{n_y}{n_z} bf=−nzny, c f = n x x 0 + n y y 0 + n z z 0 n z c_f=\frac{n_xx_0+n_yy_0+n_zz_0}{n_z} cf=nznxx0+nyy0+nzz0,初始化后的平面视差值为上图(a)右中下方的“雪花点”。
2. 迭代传播(Iteration)
一次迭代过程中,每个像素点会运行四个阶段:(1)空间传播(2)视图传播(3)时序传播(4)平面优化,首先处理左帧的所有像素,然后处理右图像的所有像素。在偶数迭代中,我们从左上角的像素开始,按行优先顺序遍历像素,直到到达右下角的像素;在奇数迭代中,我们颠倒顺序,即我们从右下角的像素开始,在左上角的像素处停止。
2.1 空间传播(Spatial Propagation)
这种传播形式背后的想法是空间相邻像素可能具有相似的平面,令 p p p表示当前像素, f p f_p fp表示其对应平面,接下来评估将 p p p分配给空间邻近点 q q q的对应平面 f q f_q fq是否能够提高代价函数的值,如果 m ( p , f q ) < m ( p , f p ) m(p,f_q)
2.2 视图传播(View Propagation)
接着利用左右视差图之间存在的强相干性,即视图中的像素及其另一个视图中的匹配点可能具有相似的平面;根据当前平面检查第二个视图中所有将当前像素 p p p作为匹配点的像素,对于像素 p p p的某个对应点 p ′ p' p′以及其平面 f p ′ f_{p'} fp′,若 m ( p , f p ′ ) < m ( p , f p ) m(p,f_{p'})
2.3 时序传播(Temporal Propagation)
这种传播形式只能在处理立体视频序列时使用,该思路假设当前视频帧的像素 p p p和前一个或连续图像中相同坐标的像素 p ′ p' p′可能具有相似的平面。若 m ( p , f p ′ ) < m ( p , f p ) m(p,f_{p'})
2.4 平面优化(Plane Refinement)
该步骤的目的是通过优化位于像素点 p = ( x 0 , y 0 ) p=(x_0,y_0) p=(x0,y0)的视差平面 f p f_p fp参数以便进一步降低代价函数的值。首先将 f p f_p fp转换为点+法线向量的表示方法,并且提出两个新参数:
- Δ z 0 m a x \Delta^{max}_{z_0} Δz0max——定义了3D点z轴坐标 z 0 z_0 z0的最大变化范围,紧接着在 [ − Δ z 0 m a x , Δ z 0 m a x ] [-\Delta^{max}_{z_0},\Delta^{max}_{z_0}] [−Δz0max,Δz0max]区间内随机取一个值 Δ z 0 \Delta_{z_0} Δz0作为修正: z 0 ′ = z 0 + Δ z 0 z_0'=z_0+\Delta_{z_0} z0′=z0+Δz0,由此得到新的3D点 P ′ = ( x 0 , y 0 , z 0 ′ ) P'=(x_0,y_0,z_0') P′=(x0,y0,z0′);
- Δ n m a x \Delta^{max}_n Δnmax——定义了法向量 n ⃗ \vec{n} n各分量的可变化范围,然后,在 [ − Δ z 0 n , Δ z 0 n ] [-\Delta^{n}_{z_0},\Delta^{n}_{z_0}] [−Δz0n,Δz0n]区间内随机取三个值组成法向量修正 Δ ⃗ n \vec{\Delta}_n Δn: n ′ ⃗ : = u ( n ⃗ + Δ n ⃗ ) \vec{n'}:=u(\vec{n}+\vec{\Delta_n}) n′:=u(n+Δn);
通过修正后的 P ′ P' P′和 n ′ ⃗ \vec{n'} n′,计算并比较代价函数,若 m ( p , f p ′ ) < m ( p , f p ) m(p,f'_p)
平面优化步骤是迭代进行的,初始设置 Δ z 0 m a x = m a x d i s p / 2 \Delta^{max}_{z_0}=maxdisp/2 Δz0max=maxdisp/2(maxdisp为设置的最大视差值), Δ n m a x = 1 \Delta^{max}_{n}=1 Δnmax=1;每次迭代后,设置 Δ z 0 m a x = Δ z 0 m a x / 2 \Delta^{max}_{z_0}=\Delta^{max}_{z_0}/2 Δz0max=Δz0max/2, Δ n m a x = Δ n m a x / 2 \Delta^{max}_{n}=\Delta^{max}_{n}/2 Δnmax=Δnmax/2,由此来逐渐缩小搜索空间。
总结
以上就是PatchMatch匹配算法中的创新部分,论文里还有一小节是讲视差后处理的,由于后处理的方法很多,常见的就几种,每个匹配算法或多或少都会用到几种后处理的方法,所以在具体的算法解读中就不做赘述,而是会单独介绍一下常见的后处理方法。本人已经开学,所以时间精力有限,接下来可能会将SGM和PatchMatch的代码注释更完,紧接着就会进行其他方面的学习,欢迎大家一同学习讨论~
参考文献和资料
[1]78. 三维重建12-立体匹配9,经典算法PatchMatchStereo
[2]【理论恒叨】【立体匹配系列】经典PatchMatch: (1)Slanted support windows倾斜支持窗模型
[3]PatchMatch Stereo - Stereo Matching with Slanted Support Windows