深度学习入门 | Self-attention&RNN&LSTM
文章目录
- 词汇转为向量,即Word Embedding
-
-
-
- cbow
- skip-gram
-
-
- 声音讯号转为向量
- Self-attention
-
-
- 提出背景
- Self-attention原理
-
- 计算相关性
- self-attention计算过程
- self-attention和CNN
-
- RNN
-
- RNN两种网络类型(Jordan network和Elman network)
- 双向神经网络(Bidirectional RNN)
- LSTM
-
- LSTM解决了RNN什么缺点
- 梯度爆炸的解决方案
-
- 梯度消失的解决方案
- LSTM常见面试题
- github项目
词汇转为向量,即Word Embedding
问题来了,如何把输入的词汇变成向量形式?这个把词汇转为向量的操作,我们就称为Word Embedding。事实上,可以有好几种,其中最简单的就是One-hot Encoding
- One-hot Encoding:例如把apple = [ 1 0 0 0 0 …… ];bag = [ 0 1 0 0 0 …… ];cat = [ 0 0 1 0 0 …… ],但词语之间的相关性会丢失。
- word2vec:这是通过神经网络的模型去得到的向量,下面介绍两个经典的word2vec的方式,分别是cbow和skip-gram,一个是利用上下文预测中心词,一个是利用中心词预测上下文。
cbow
假设语料库一共有V个词, 每个词在语料库中取其上下文中共C个词作为它的上下文。每个词最终使用N维的embedding来表达。
- 输入部分: 那么神经网络的输入就是这C个上下文的词,每个词简单的用one-hot representation. 设每个词的向量大小是1 * V. 所以输入一共是C* V向量
- 隐藏层:隐藏层大小为VN,于是 C * V个向量,与V * N的矩阵相乘,乘完之后把输出的向量大小为CN,对每列求平均即每个上下文词求平均, size是1 * N。这里的1 * N的向量我们就视为中心词的word-embedding
- NN的输出层:将隐层乘以一个N * V的矩阵产出一个1 * V的向量,并做softmax, 作为所有词的概率表示。
- 求LOSS:将上面的output与当前的目标词的one-hot representation求loss.
skip-gram
模型的结构如下:
- 输入层:目标词语基于词库做one-hot编码的词向量,size为1×N;
- 输入层→隐藏层:做线性变换的权重矩阵,size为 N × M,且 M < < N;
- 隐藏层:size为 1 × M的向量,即目标词语的词向量;
- 隐藏层→输出层:做线性变换的权重矩阵,size为 M × N ;
- 激活函数:采用了softmax函数;
- 输出层:目标词与词库中所有词是上下文关系的概率,size为 1 × N .
这里的输入为 1×N 的向量(即词库中词语总量为N),输入层到隐藏层的权重矩阵为 N×M(其中M< 针对输入的向量不是一个,而是一排,且输入向量个数会改变,比如说输入一句话,这句话有很多词汇,那么输入向量就是不确定长度的。 当然输出也有很多种类型,主要有以下几种: 输入和输出维度一致,即输入N维输出N维。应用场景如词性标注 输入多维,输出一维。应用场景如抓取一段文字,判断情绪是积极还是消极 输入多维,输出多维,称为seq2seq。应用场景如语言翻译 我们下面比较关注的是第一种,也就是输入N维输出N维,每个词语都输出一个label。因为词语之间是有联系的,我们希望能学习到多个词语,最简单的想法就是搞个window,对于某个词把其相邻window个的一起词放进fully-connect输出一个Window,但是我们输入的词语序列长度是不固定的,没法确定window的大小是多少比较合适。于是,我们需要提出新的模型,即Self-attention Self-attention是考虑一整个序列后才得到输出的,可以进行多次Self-attention操作,例如下图输入序列后,进行self-attention学习一整个序列信息后输出到fully-connect层,然后你可以再使用self-attention把这个序列信息再处理一次,然后交替使用self-attention和fully-connect,最后输出label。 下面,我们来看具体的self-attention长什么样子。 刚才分析过,我们可以做多层self-attention,因此其输入不一定是原始序列,可能是处理过后的隐藏层输出,所以我们把输入用 α i \alpha_i αi表示而不是 x i x_i xi。而self-attention考虑整个序列的信息最后才输出label的,那么如何考虑整个序列信息呢?以生成 b 1 b_1 b1举例,这里就需要我们分析整个序列中每个元素与 α 1 \alpha_1 α1的相关性。 简单的介绍下以下两种,我们用的是左边比较简单的那种。 左边算法,对于输入的两个数据 α 1 , α 2 \alpha_1,\alpha_2 α1,α2,我们分别乘上矩阵 W q W_q Wq和 W k W_k Wk,得到新的向量 q q q和 k k k, q q q和 k k k的点乘(内积)就是所求的相关性。 而右边是 q q q和 k k k相加后做tanh,再与矩阵W相乘后得到相关性 我们假设输入的向量只有 α 1 , α 2 . . . , α 4 \alpha_{1},\alpha_{2}...,\alpha_{4} α1,α2...,α4共四个。 计算 b 1 b_1 b1主要分为两部分,一是计算 α 1 , α 2 . . . , α 4 \alpha_{1},\alpha_{2}...,\alpha_{4} α1,α2...,α4与 α 1 \alpha_{1} α1的相关性,如 α 12 \alpha_{12} α12,再将这个相关性进行soft-max处理得到 α 12 ′ \alpha'_{12} α12′。二是将每个输入向量乘 v i v_i vi再与将soft-max处理后的 α 12 ′ \alpha'_{12} α12′相乘,这些求和之后得到的就是 b 1 b_1 b1。具体过程如下图所示。 cnn是self-attention的特殊化,通过设置self-attention可以做到cnn的所有工作。 self-attention是关注全局的关系,cnn是关注指定范围内互相的关系。 输入 x 1 = [ 1 , 1 ] x_1=[1,1] x1=[1,1]时,经过U变成[2,2],加上W=[0,0],把[2,2]存储到W中去;下一个输入 x 2 = [ 1 , 1 ] x_2=[1,1] x2=[1,1]时,经过U变成[2,2],加上W=[2,2],得到的S为[3,3],把[3,3]存储到W中去以此类推 注意的是,每次新的输入进去,经过U作用得到的值加入到W时,将原本W中有的值覆盖掉了。因此RNN是短记忆性,接下来我们介绍具有长记忆性的RNN,成为LSTM https://blog.csdn.net/qq_31375855/article/details/106795105 递归神经网络有两种类型:Jordan network和Elman network,现在常用的RNN(包括LSTM、GRU等等)都是用Elman network。 它们都是很久以前的奠基性工作了,所以都是基于最浅的三层网络结构定义的。 Elman network的一个recurrent层的输出经过时延后作为下一时刻这一层的输入的一部分,然后recurrent层的输出同时送到网络后续的层,比如最终的输入层。 而Jordan network则直接把整个网络最终的输出(i.e. 输出层的输出)经过时延后反馈回网络的输入层 分别正向和反向遍历,共同输出的再进行一次遍历。优点在于产生output的时候,普通的RNN给定当前词他可能仅仅看了过去的内容,而双向RNN不仅看了前面的还看了后面的内容。 长短期记忆(Long short-term memory, LSTM)是一种特殊的RNN,主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说,就是相比普通的RNN,LSTM能够在更长的序列中有更好的表现。 首先,输入 x 1 = [ 3 , 1 , 0 ] x_1=[3,1,0] x1=[3,1,0],经过 g ( z ) g(z) g(z)操作得到 ( 1 ∗ 3 + 0 ∗ 1 + 0 ∗ 0 ) + 0 ∗ 1 = 3 (1*3+0*1+0*0)+0*1=3 (1∗3+0∗1+0∗0)+0∗1=3, x 1 x_1 x1和 z i z_i zi向量相乘得到 ( 0 ∗ 3 + 100 ∗ 1 + 0 ∗ 0 ) − 10 = 90 (0*3+100*1+0*0)-10=90 (0∗3+100∗1+0∗0)−10=90,经过soft-max返回概率趋近于1,说明存储开关开放,我们把值3存入cell中。再看记忆开关, x 1 x_1 x1和 z f z_f zf向量相乘得到 ( 0 ∗ 3 + 100 ∗ 1 + 0 ∗ 0 ) + 10 = 110 (0*3+100*1+0*0)+10=110 (0∗3+100∗1+0∗0)+10=110,经过soft-max返回概率趋近于1,说明记忆开关开放,我们把值cell中的3*1=3。最后看释放开关, x 1 x_1 x1和 z o z_o zo向量相乘得到 ( 0 ∗ 3 + 0 ∗ 1 + 100 ∗ 0 ) − 10 = − 10 (0*3+0*1+100*0)-10=-10 (0∗3+0∗1+100∗0)−10=−10,经过soft-max返回概率趋近于0,说明释放开关关闭,我们把值cell中3无法释放出去,所以 y 1 = 0 y_1=0 y1=0。 同理,输入 x 2 = [ 4 , 1 , 0 ] x_2=[4,1,0] x2=[4,1,0],经过 g ( z ) g(z) g(z)操作得到4,存储开关开启,记忆开关开启,因此此时cell中值Wie3+4=7,释放开关关闭,所以 y 2 = 0 y_2=0 y2=0。 接着,输入 x 3 = [ 2 , 0 , 0 ] x_3=[2,0,0] x3=[2,0,0],经过 g ( z ) g(z) g(z)操作得到2,存储开关关闭,记忆开关关闭,此时cell中值还是7,释放开关关闭,所以 y 3 = 0 y_3=0 y3=0。 接着,输入 x 4 = [ 1 , 0 , − 1 ] x_4=[1,0,-1] x4=[1,0,−1],经过 g ( z ) g(z) g(z)操作得到1,存储开关关闭,记忆开关关闭,此时cell中值还是7,但是释放开关开放,所以 y 4 = 7 y_4=7 y4=7。 参考: https://blog.csdn.net/u012744245/article/details/112378232(RNN的梯度消失和梯度爆炸) RNN很容易出现梯度消失或爆炸的问题,梯度消失和梯度爆炸本质是同一种情况。梯度消失经常出现的原因:一是使用深层网络;二是采用不合适的损失函数,如Sigmoid。梯度爆炸一般出现的场景:一是深层网络;二是权值初始化太大。 深层网络由许多非线性层堆叠而来,每一层网络激活后的输出为 f i ( x ) f i ( x ) fi(x) ,其中 i 为第 i层, x 是第 i层的输入,即第 i − 1层的输出, f 是激活函数,整个深层网络可视为一个复合的非线性多元函数: f n ( . . . f 2 ( f 1 ( x ) ) ) ) f_n(...f_2(f_1(x)))) fn(...f2(f1(x))))。 我们在RNN中使用的激活函数是sigmod函数,而sigmod函数在求导时有个很严重的问题,就是导数值最大是0.25,假设s是sigmod函数,则 s ′ = s ( 1 − s ) ≤ 0.25 s'=s(1-s)\leq 0.25 s′=s(1−s)≤0.25,反向传播随着层数增加,梯度更新将以指数形式衰减,即发生梯度消失。反之如果我们求导大于1就会发生梯度爆炸。 需要注意的是,RNN和DNN梯度消失和梯度爆炸含义并不相同。RNN中权重在各时间步内共享,最终的梯度是各个时间步的梯度和。因此,RNN中总的梯度是不会消失的,即使梯度越传越弱,也只是远距离的梯度消失。 RNN所谓梯度消失的真正含义是,梯度被近距离梯度主导,远距离梯度很小,导致模型难以学到远距离的信息。 明白了RNN梯度消失的原因之后,我们看LSTM如何解决问题的呢? 我们采用LSTM就可以避免者消失,主要原因在于LSTM内部复杂的“门”(gates),RNN每次的记忆都会被最新的输入覆盖掉,而LSTM通过它内部的“门”可以在更新的时候“记住”前几次训练的“残留记忆”,也就是说LSTM会存储过往的以及来消除近距离梯度的影响。但是LSTM没办法很好的解决梯度爆炸的问题,所以我们在训练LSTM的时候,往往把learning rate设小一些。 https://blog.csdn.net/u012744245/article/details/112378232(RNN的梯度消失和梯度爆炸) https://blog.csdn.net/qq_38147421/article/details/107692418 https://github.com/vsmolyakov/experiments_with_python声音讯号转为向量
Self-attention
提出背景
Self-attention原理


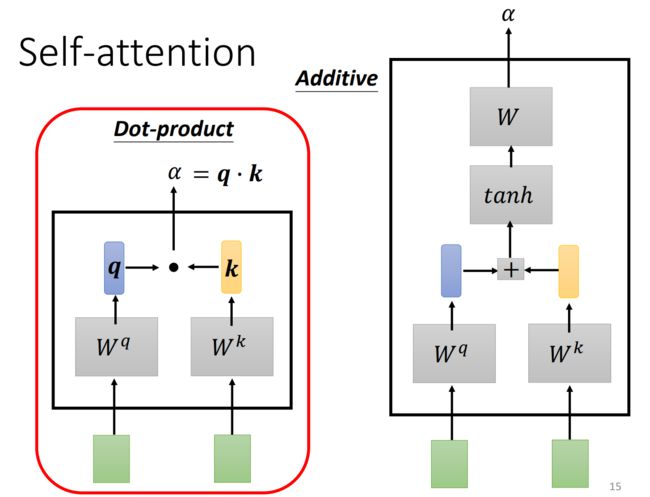
计算相关性
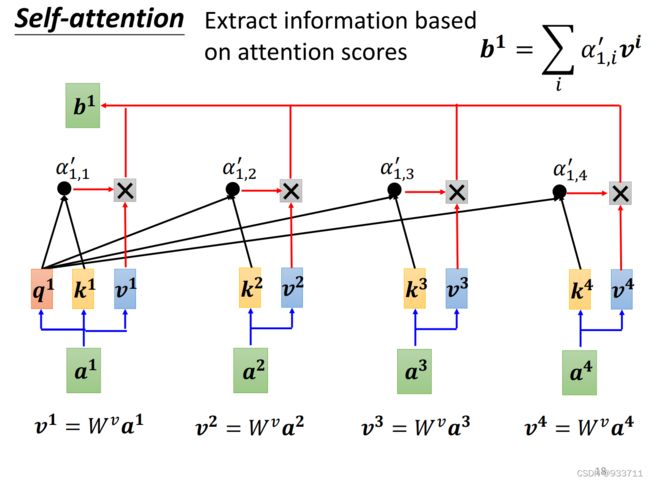
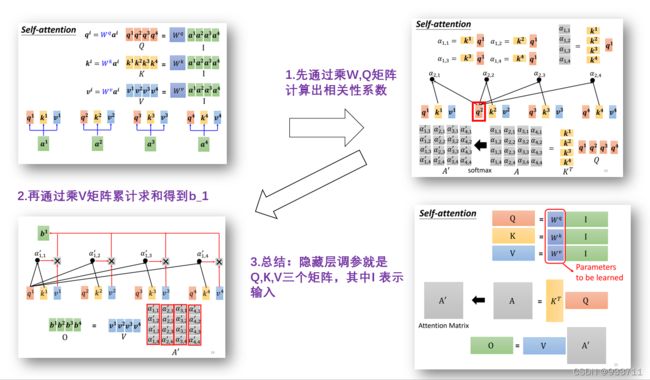
self-attention计算过程
self-attention和CNN

RNN
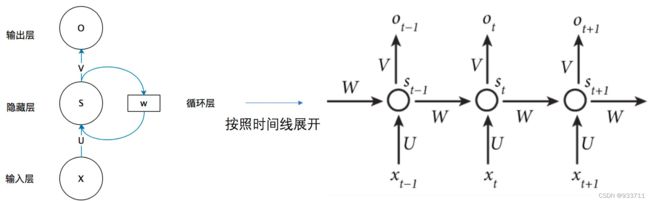
举例,我们输入的x是[[1,1],[1,1],[2,2]],初始W=[0,0],U,W都是线性相加,即U,W=[[1,1],[1,1]],如果 x 1 = [ x 11 , x 12 ] x_1=[x_{11},x_{12}] x1=[x11,x12],经过U之后是变成 [ x 11 + x 12 , x 11 + x 12 ] [x_{11}+x_{12},x_{11}+x_{12}] [x11+x12,x11+x12]RNN两种网络类型(Jordan network和Elman network)
 它们的区别是:
它们的区别是:
双向神经网络(Bidirectional RNN)

LSTM
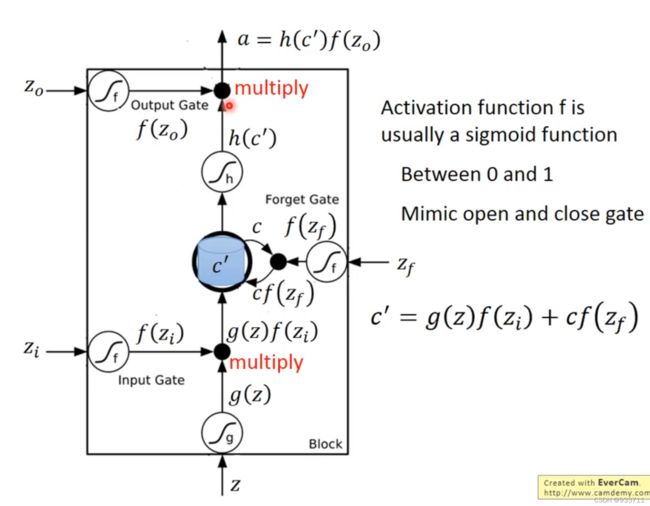
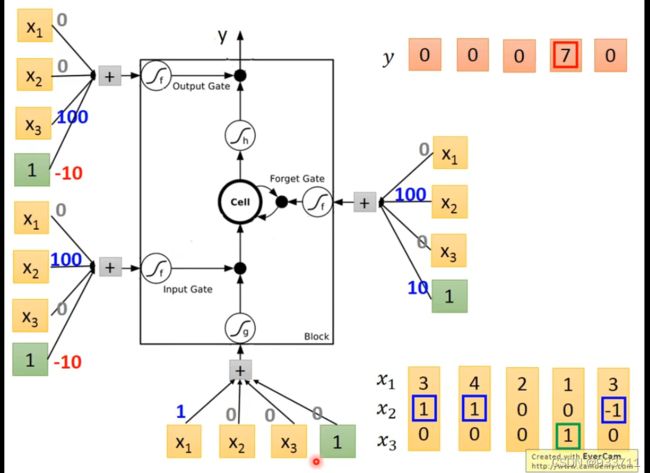
我们举例说明,输入向量是[[3,1,0],[4,1,0]…]如右下角所示,分别控制存储、记忆和释放的向量,即上图中的 z i , z f , z o z_i,z_f,z_o zi,zf,zo,向量值是[0,100,0,-1],[0,100,0,10],[0,100,0,-10]。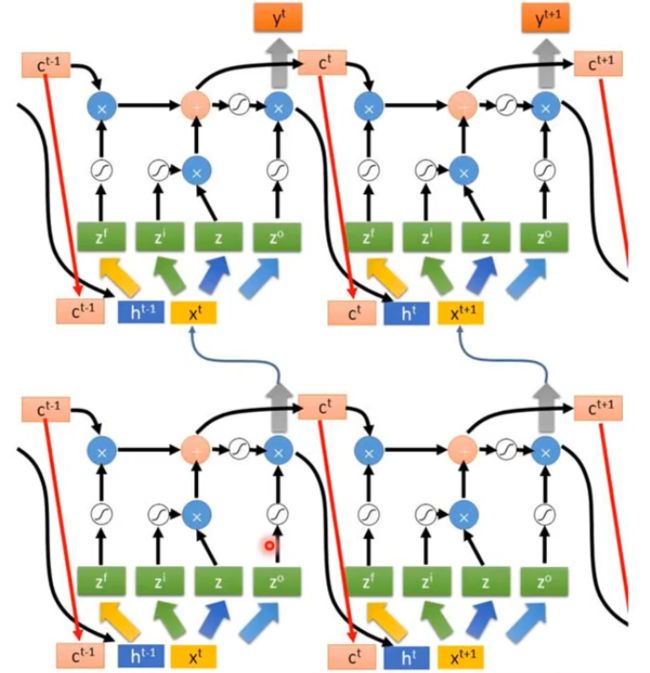
LSTM解决了RNN什么缺点
https://blog.csdn.net/XiaoYi_Eric/article/details/105751692
梯度爆炸的解决方案
梯度消失的解决方案
LSTM常见面试题
github项目