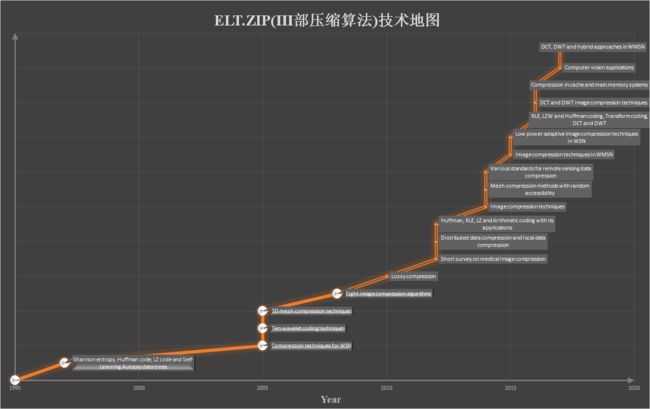
【ELT.ZIP】OpenHarmony啃论文俱乐部——轻翻那些永垂不朽的诗篇

• 本文出自ELT.ZIP团队，ELT<=>Elite(精英)，.ZIP为压缩格式，ELT.ZIP即压缩精英。
• 成员：
  • 上海工程技术大学大二在校生
  • 合肥师范学院大二在校生
  • 清华大学大二在校生
  • 成都信息工程大学大一在校生
  • 黑龙江大学大一在校生
  • 山东大学大三在校生
• 我们是来自6个地方的同学，我们在OpenHarmony成长计划啃论文俱乐部里，与华为、软通动力、润和软件、拓维信息、深开鸿等公司一起，学习和研究操作系统技术…

---

【往期回顾】

 ① 2月23日 《老子到此一游系列》之 老子为什么是老子 —— 综述视角解读压缩编码
 ② 3月11日 《老子到此一游系列》之 老子带你看懂这些风景 —— 多维探秘通用无损压缩

【本期看点】

主题：《老子到此一游系列》之 老子见证的沧海桑田

• 塞缪尔·莫尔斯发明摩斯密码开创编码领域先河
• 香农提出信息熵，用数学语言阐明了概率与信息冗余度的关系
• 用生活中的烹饪视角解析Huffman编码过程
• 小波系数的各类编码方案大比拼
• 计算机视觉中的女神 —— Lenna
• 当代无线传感器型网络数据压缩
  

【技术DNA】

【智慧场景】

【脉动一下】

---

数据压缩理论缘起

起源

• 数据压缩概念的演变源于摩尔斯电码，也即我们日常所说的摩斯密码（SOS就是其中一种），它是一种时通时断的信号代码，通过不同的排列顺序来表达不同的英文字母、数字和标点符号，从而最小化消息的大小和传输时间。由电报之父塞缪尔·莫尔斯于1837年发明，1838年正式用于压缩电报中的信件。

发展

• 1986年Richard W. Hamming编写出版的《Coding and information theory》一书中提到：++编码和信息理论的概念起源久远，但在信息理论还未建立起一个坚实的基础之时，人们对其的许多基础性想法与理解其实都只停留在1948年之前。++
• 说到信息理论，不得不提到一个人 —— Claude E. Shannon(克劳德·艾尔伍德·香农)。香农是美国数学家，也是信息论的创始人，他提出了信息熵的概念，为信息论和数字通信的发展奠定了基础。从本质上讲，数据压缩的目的就是要消除信息中的冗余，而信息熵及相关的定理恰恰用数学手段精确地描述了信息冗余的程度。利用信息熵公式，人们可以计算出信息编码的极限，即在一定的概率模型下，无损压缩的编码长度不可能小于信息熵公式给出的结果。
  于是后来，上述形势被1948年香农发表的两篇名为《通讯的数学原理》的文章所打破，它们在信息理论领域几乎迅速地传播并流行了起来。很快，另外一些信息理论的文章出现在了相关期刊上，许多大学的电气工程等相关部门也开始教授相关课程。
  但由于信息理论在当时是一个新领域，人们对其能做的事情以及能应用的方向还没有一个确切的认识，渐渐地，人们对其的关注度愈发降低，相关课程的教授也随之减少。

转折

• 信息理论具有广泛适用于远离其原始灵感的情况的想法。好巧不巧的是，在信息理论被创立的左右之时，编码理论也诞生了。就编码理论而言，其数学背景在一开始远没有信息理论那么复杂，而且在很长一段时间里，它也没有得到理论界的重视。但是，随着时间的推移，各种数学工具如群论、有限域理论等慢慢被应用到编码理论中。现在，编码理论已成为数学研究中一个活跃的部分。

从逻辑上讲，编码理论引出了信息论，信息论提供了对信息进行适当编码所能做的操作的界限。因此，这两种理论是密切相关的。

• 1948 年，香农在提出信息熵理论的同时，也给出了一种简单的编码方法—— Shannon 编码，为压缩算法领域的发展奠定了专属基调。 1952 年， R. M. Fano 又进一步提出了 Fano 编码。这些早期的编码方法揭示了变长编码的基本规律，也确实可以取得一定的压缩效果，但离真正实用的压缩算法还相去甚远。
  第一个实用的编码方法是由 D. A. Huffman 在 1952 年的论文《最小冗余度代码的构造方法（ A Method for the Construction of Minimum Redundancy Codes ）》中提出的。直到今天，许多《数据结构》教材在讨论二叉树时仍要提及这种被后人称为 Huffman 编码的方法。 Huffman 编码在计算机界是如此著名，以至于连编码的发明过程本身也成了人们津津乐道的话题。据说， 1952 年时，年轻的 Huffman 还是麻省理工学院的一名学生，他为了向老师证明自己可以不参加某门功课的期末考试，才设计了这个看似简单，但却影响深远的编码方法。
  Huffman 编码效率高，运算速度快，实现方式灵活，从 20 世纪 60 年代至今，在数据压缩领域得到了广泛的应用。例如，早期 UNIX 系统上一个不太为现代人熟知的压缩程序 COMPACT 实际就是 Huffman 0 阶自适应编码的具体实现。 20 世纪 80 年代初， Huffman 编码又出现在 CP/M 和 DOS 系统中，其代表程序叫 SQ 。今天，在许多知名的压缩工具和压缩算法（如 WinRAR 、 gzip 和 JPEG ）里，都有 Huffman 编码的身影。不过， Huffman 编码所得的编码长度只是对信息熵计算结果的一种近似，还无法真正逼近信息熵的极限。正因为如此，现代压缩技术通常只将 Huffman 视作最终的编码手段，而非数据压缩算法的全部。

Huffman码

• 说到哈夫曼编码或是霍夫曼编码，热爱自然科学、关注计算机科学的朋友们，或许曾听过、研究过；若是第一次听闻，或许会有一种像听到相对论、量子力学等一般的紧张感，请不必担心，我们接下来以一种老少皆宜、通俗有趣的方式传播分享，通读一遍说不定也能收获满满，接下来让我们进入正题吧：
• 先来感性地认识一下霍夫曼编码，首先顾名思义，我们可以明确一个大前提，这是霍夫曼的作品，其次这是一种编码技术。技术是用来解决问题的，那霍夫曼编码是用来解决什么问题的呢？——信息压缩问题。
• 现在大家心中已经对霍夫曼编码建立起了一个最基本的概念，这是由霍夫曼创立的用于解决信息压缩问题的编码技术。但这个概念还是太笼统了，再详尽一些是什么样子的呢？（别紧张，接下来你不会看到满屏的数学公式）。
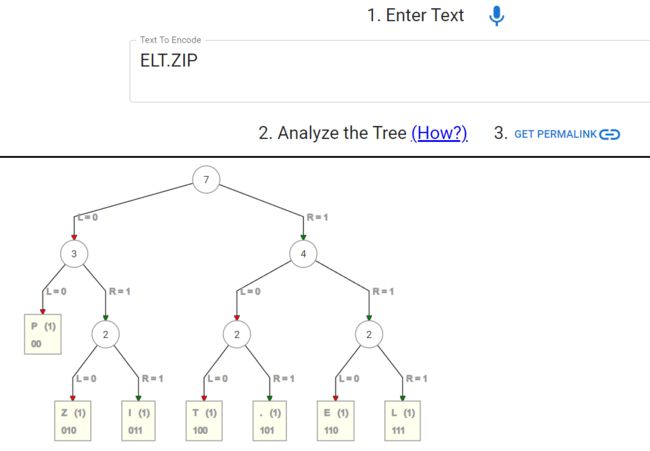
• 我们用烹饪来举个例子，大家或许做过，或者看别人做过饭，做饭首先就得明确目标，就是我要做什么菜，对于霍夫曼编码来说就是目标压缩文本是什么，然后你就得列个清单看看做这道菜需要哪些原材料，各种要多少；对于霍夫曼编码来说就是一个统计构成文本的元素的种类和出现频率的过程；料备齐了就要掌握如何搭配，以及掌握火候，这就是考验一个人的厨艺的时候了；对于霍夫曼编码来说就是建立一个高效的字典树的过程。这一套流程下来我们可以获得一个菜的菜谱，这就是一个成品菜的压缩成果；对于霍夫曼来说我们就获得了一个文本的字典树：
  

在线体验霍夫曼编码生成过程：
huffman.ooz.ie - Online Huffman Tree Generator (with frequency!)

现代场景

1. 汉字字形压缩

• 通俗些说就是把我们的中文文本进行识别和压缩，这与英文文本有什么不同呢？中华文化博大精深，不像英文文本只有26个字母和一些标点符号，汉字千变万化，无法通过传统的方式统计编码。但是万变不离其宗，我们从小写字就知道一点，我们的汉字是由笔划再按照一定笔顺写成的，那么这时笔划也就是我们前面所说的原材料模板：
  

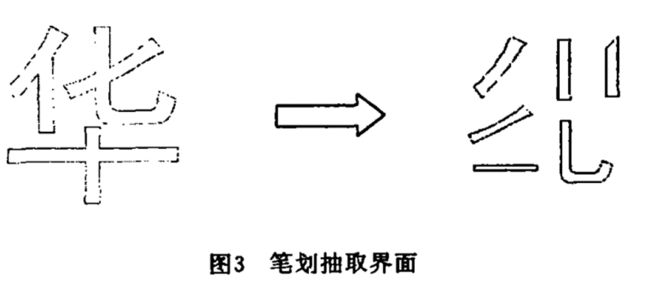
而笔顺就是我们建立字典的依据，我们的汉字通过这样的处理就可以通过霍夫曼编码进行压缩编码了。

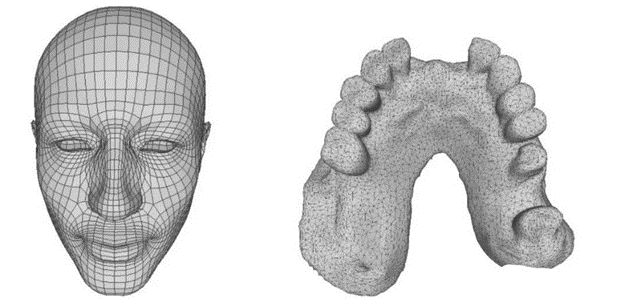
2. 3D网格的编码压缩

• 说到3D网格大家脑海中最先会联想到的可能会是3D动画，没错这一项技术广泛的应用于这一领域，下面一些图片可供直观感受：
  
  

那么如何让这些精美的3D作品高效的压缩存储呢？霍夫曼编码大显身手的时侯
到了，下面介绍相关场景并补充一项3D网格几何压缩的强大算法。

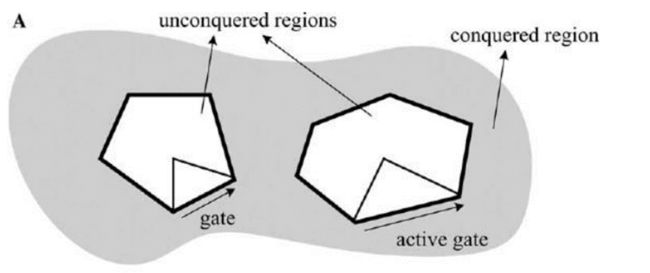
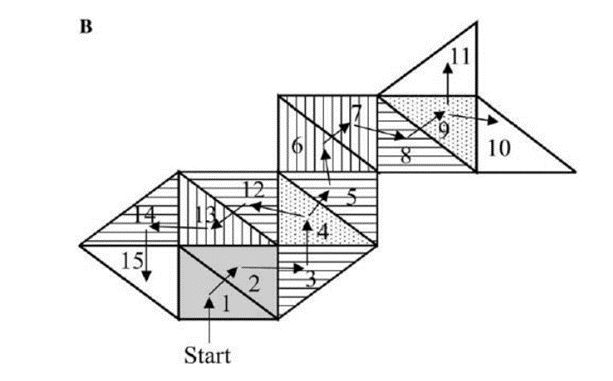
【征服三角形】

• 对未征服也就是未编码之处围绕其边界插入三角形，进行拟合重构
  

• 其中箭头和数字给出了三角形征服的顺序。三角形中填满了不同图案来代表不同的操作码，当它们被征服时就会生成这些操作码，再通过霍夫曼进行处理
  

【kD-tree分解（强大的3D图像处理算法）】

• 该方案特别适用于地形模型和密集采样对象
  

• 为便于理解我们用2D来表述
  

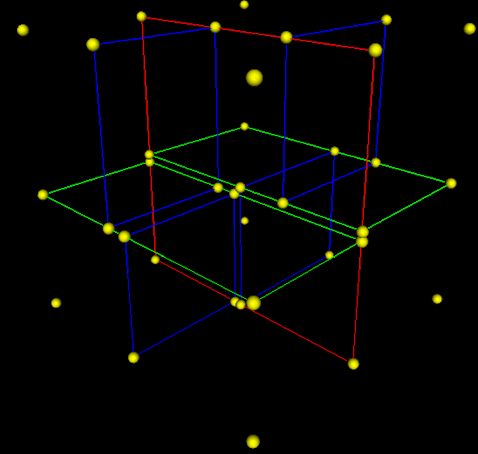
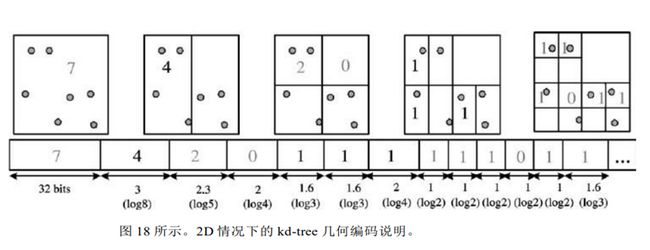
• 每次将一个单元格细分为两个小单元格，对顶点数量进行编码。这种细
  分被重复地应用，直到每个单元格足够小，可以只包含一个顶点，并能够足够精确地重建顶点位置。

动态Huffman码的设计

• 动态哈夫曼编码（Dynamic Huffman coding），又称适应性哈夫曼编码（Adaptive Huffman coding），是基于哈夫曼编码的自适应编码技术。它允许在符号正在传输时构建代码，允许一次编码并适应数据中变化的条件，即随着数据流的到达，动态地收集和更新符号的概率（频率）。一遍扫描的好处是使得源程序可以实时编码，但由于单个丢失会损坏整个代码，因此它对传输错误更加敏感。

摘要

• 文章介绍并分析了一种构造动态Huffman码的单遍算法，同时还分析了由 Faller、Gallager和Knuth 三位学者得到的单遍算法。在每个算法中，发送器和接收器都保持等效的动态变化 Huffman 树，并对其进行实时编码。他们证明了新算法编码包含 t 个字母的消息所占用的bit数小于t，远远优于传统的两遍 Huffman 方案，并且与字母表的大小没有关系。对于任何一种单遍 Huffman 算法来说，这是在最坏状态下能做到的最佳可能情况。实验表明，新算法生成的编码长度比其他单遍算法的短，除了长消息外，也比两遍算法的短。最后明确了该算法适用于数据网络的在线编/解码和文件压缩场景。

介绍

• 由于传统的静态 Huffman 算法存在一个缺点，即它需要对数据进行两次遍历：第一次是通过构造和传输 Huffman 树到接收器，来收集消息中字母出现的频率计数；然后第二次再基于第一次构造的静态树结构，来编码和传输消息本身。那么，这会导致在将其用于网络通信时产生延迟，或者在文件压缩应用程序中产生额外的磁盘访问从而减慢算法。所以，Faller 和 Gallager两人各提出了一种一次遍历方案，后来被 Knuth 大大改进，以构造动态 Huffman 编码。发送器用来编码消息中第 t + 1 个字母的二叉树(同时也是接收器用来重建第 t + 1 个字母的二叉树)是消息前 t 个字母的二叉树。这样的话，发送器和接收器就都会从相同的初始树开始，发送器永远不需要将树发送给接收器。很显然，这与两次遍历算法的情况不同。
• 随后，研究者设计并证明了一个所有单遍Huffman方案中，在最坏情况下表现仍然是最优的算法A，它可以用于网络通信的通用编码方案，也可以作为基于文字的压缩算法中的一种高效子例程。
  
  

实验结论

算法A的优点：

1. 对于编码效率差异相对较大的小消息，每个字母占用更少的位
2. 在 t 小于10⁴时，相比所有两遍算法都表现得更好
3. 能够对消息进行实时编码解码，每个字母使用不到一个额外的比特位对消息进行编码
4. 在文件压缩、网络通信和硬件实现方面有很大的应用潜力
5. 可用来增强其他压缩方案

小波系数图像压缩编码

引言

• 由于多媒体信息和数字化的图像表示形式所带来的网络流量的不断增加，图像压缩已经成为一种刚需。基于小波的图像压缩新算法被开发出来，这些方法取得了实际性进展，如：卓越的低比特率性能、连续音调和比特级压缩、无损和有损压缩、逐像素、精度和分辨率传输等。小波算法最成功的应用之一是基于变换的图像压缩，其重叠特性减轻了块效应（马赛克被放大的场景）；而小波分解的多分辨率特性又使解压后的图像具有更好的感知质量。前期相关文章已经涉及到小波变换的部分内容，这里再继续对其展开详细描述。

基本原理

• 大多数图像的共同特征是相邻像素是相关的，所以便包含了很多冗余信息。然后，最重要的任务是找到图像中不太相关的表示。压缩的两个基本组件就是冗余和无关性的减少：
  • 冗余减少的目的是消除信号源（图像/视频）的重复
  • 无相性的减少则是忽略了信号接收器即人类视觉系统（HVS）通常不会注意到的部分信号
• 另外，通常也有三种类型的冗余：
  • 相邻元素之间的空间冗余或相关性
  • 不同颜色平面或光谱带之间的光谱冗余或相关性
  • 图像序列相邻帧之间的时间冗余或相关性（主要就是视频应用）

因此，图像压缩的目标就是希望尽可能地去除空间和光谱冗余以减少表示图像所需的比特位数。其次，图像压缩还需保证一个基本目标：降低传输或存储比特率的同时保持可接受的保真度或图像质量。

高低频分离&&量化

• 大多数自然图像都有平滑的颜色变化，在平滑变化之间，精细的细节被表示为尖锐边缘。从技术上讲，颜色的平滑变化被称为低频变化，尖锐变化被称为高频变化。低频成分构成了图像的基础，高频成分则是为了细化图像。因此，基础比细节相对更重要。类似的，我们在声乐领域也能找到相对应的概念 —— 基音与泛音，基音是波形里振幅最大，频率最小的组成波，它决定了音高；而泛音频率是基音的整数倍，跟基音叠加在一起后整体波形仍是基音的频率，但加入泛音组成后波形的形态不再单纯，可以理解为对基音作了一定的修饰，即决定了音色。
• 分离多数采用离散小波变换（DWT），通过滤波器组对图像进行一系列类似金字塔型的操作。基于小波的编码在传输和解码错误下具有更强的鲁棒性，有利于图像的渐进传输。此外，它们也更符合人类视觉系统的特点。
• 量化，是指用有限的、较小的值集来逼近图像数据中连续的值集的过程。有两种类型的量化，分别是标量量化和矢量量化。

度量指标

• 两类用于比较各种图像压缩技术的指标是均方误差（MSE）和峰值信噪比（PSNR），MSE值越小，误差越小；PSNR值越大，信噪比越高，其中，“信号”是原始图像，“噪声”是重建时的误差。因此，具有较低MSE和较高PSNR的压缩方案可被认为是较好的压缩方案。

小波系数的各类编码方案

嵌入式零树小波编码（EZW）

• EZW是最早展现基于小波图像压缩的全部能力的算法之一，其编码器基于渐进式编码，将图像压缩成一个bit流。因为渐进编码又叫做嵌入式编码，所以即EZW中的E。下面是EZW算法对大小为512 × 512图像的压缩比和PSNR值的结果：
  

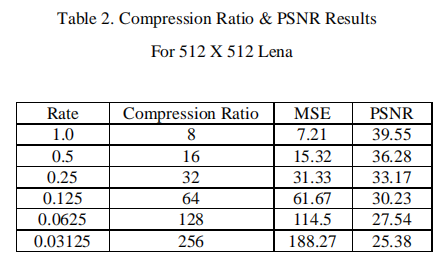
下一个方案称为 SPIHT，是 EZW 的一种改进形式，比 EZW 有着更好的压缩性能。

多级树集合分裂编码（SPIHT）

• SPIHT编码器是EZW编码的一个高度精细化版本，同样可产生嵌入的bit流。对于各类图像，SPIHT可获得最佳结果 —— 给定压缩比下，PSNR值最高。所以，它是图像压缩中最先进的基准算法。SPIHT不是传统图像压缩算法的简单扩展，它代表了该领域的一个里程碑式进展，具有以下性质：

1. 图像质量好，PSNR值高，尤其对于彩色图像
2. 是优化好的渐进式图像传输
3. 生成一个完全嵌入的编码文件
4. 简单量化算法
5. 快速编/解码（几乎对称分布）
6. 应用范围广、适应性强
7. 可用于无损压缩
8. 可以编码到精确的比特率或失真
9. 高效结合误差保护
   
   

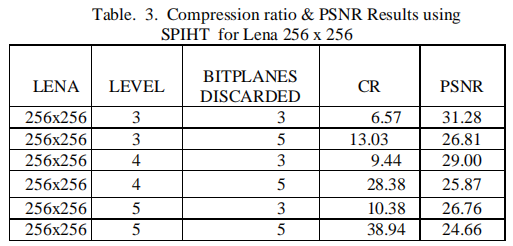
SPIHT可以通过对输出信息进行熵编码来提高效率，但代价是增加了编/解码的时间。同时为了减少此方案中使用的列表数量，需要形成下一个算法，称为 SPECK。

设置分区嵌入式块编码(SPECK)

优化截断的嵌入式块编码（EBCOT）

• EBCOT 将每个子带划分为相对较小的样本块，并生成一个独立的高度可伸缩的比特流来表示每个所谓的代码块。该算法展示了最先进的压缩性能，同时产生一个前所未有的特征集的比特流，包括分辨率和信噪比可伸缩性以及随机访问属性。该算法具有适度的复杂性，非常适合于涉及远程浏览大型压缩图像的应用。
  
  
  

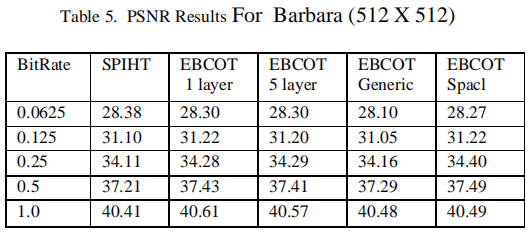
• 可见，在最先进的压缩算法方面，EBCOT显著优于SPIHT。

其他

• 此外，还有许多小波系数相关编码技术，如小波差约简（WDR）、自适应扫描小波差约简（ASWDR）、空频量化（SFQ）、嵌入式预测小波图像（EPWIC）、可逆嵌入小波压缩（CREW）、堆栈运行（SR）等，这里不再一一赘述，各种编码技术的优缺点详见下表：

类型	特性	不足
EZW	采用渐进和嵌入式传输 / 使用零树概念 / 用单个符号编码树 / 使用预定义的扫描顺序 / 良好的结果反馈	系数位置的传输丢失 / 没有真正压缩 / 依赖于算数编码器
SPIHT	广泛使用 —— 对于各类图像都有较高PSNR值 / 四叉树或层次树被设置为分区树 / 采用空间定向树状结构 / 通过三个列表跟踪索引集的状态：LSP、LIS、LIP / 采用渐进和嵌入式传输 / 在感知图像质量和PSNR值上优于JPEG	仅隐式定位有效系数的位置 / 由于三个列表致使内存需求更多 / 传输信息只由单个bit组成 / 适合各种自然图像 / 感知质量不是最优的
SPECK	不使用树 / 使用矩形块区域 / 利用频率和空间的能量聚集 / 采用渐进和嵌入式传输 / 低计算复杂度 / 采用四叉树和倍频带划分 / 由于两个列表致使内存需求低 / PSNR值优于SPIHT
EBCOT	支持数据包分解 / 基于块的方案 / 适度复杂性 / 比特流由质量层集合组成 / 信噪比具备可伸缩性 / 出色的纹理表现 / 保留SPIHT中丢失的边	性能随层数的增加而降低 / 适合远程浏览大型压缩图像
WDR	采用ROI概念 / 对重要小波变换值的位置进行编码 / 感知图像质量相比SPIHT更好 / 不用像SPIHT那样在四叉树中搜索 / 适合低比特率的低分辨率医学图像 / 低复杂度 / 高边缘相关性 / 高边缘保护性	PSNR值没有SPIHT高
ASWDR	与WDR相比更改了扫描顺序 / 可预测新关键值的位置 / 动态适应边缘细节的位置 / 相比WDR能编码更多关键值 / PSNR值优于SPIHT和WDR / 感知图像质量优于SPIHT、略优于WDR / 边缘相关性略优于WDR / 保留更多细节 / 适合如侦察或医疗类的高压缩率图像
SFQ	其量化模式直接利用了高频系数的空间聚类 / 均匀量化+熵编码提供了几乎最优的效率
CREW	适合于需要高质量的灵活性应用如医疗图像、固定速率大小的程序(ATM)、印前图像、连续色调传真、图像档案、万维网图像、卫星图像等
SR	通过光栅扫描工作从而寻址复杂度相比其他算法较低

第二代图片压缩技术

引言

• 在硬件受限的环境下，在视觉传感器节点中实现图像处理引擎一直是无线多媒体传感器网络发展的主要关注点。文章对8种常用的图像压缩技术进行了综述。综合评估后发现，基于层次树集分块(Set-Partitioning in Hierarchical tree, SPIHT)小波的图像压缩算法压缩效率高，编码过程简单，是无线传感器网络中最适合硬件实现的图像压缩算法。

无线传感器网络(WSN)图片压缩

• 无线传感器网络(Wireless sensor network, WSN)是由多个传感器设备通过无线信息进行通信的网络，具有在传感器节点上进行数据处理和计算的能力。近年来，人们对可靠、高效的无线多媒体传感器网络(Wireless multimedia sensor network, WMSN)研究和开发越来越感兴趣。从摄像机节点收集的图像和视频帧等多媒体数据需要大量的处理，这使得WMSN的实现非常困难，特别是在硬件受限的环境中。高功耗、有限带宽和内存限制是影响高效灵活WMSN开发的挑战和制约因素。
• 多媒体内容，特别是高分辨率的图像需要广泛的带宽传输。由于可用带宽有限，传感器节点捕获的图像在传输前需要进行处理和压缩。通过图像压缩去除原始数据中的冗余信息，可以获得一种更高效的传输方法。
• 最近的技术使得具有嵌入式处理能力的微型传感设备的生产成为可能。由于空间限制和提供大量内存存储的高成本，片上内存受到限制，并成为处理大型图像的另一个主要约束。因此，需要开发一种更简单、更经济的系统，以满足图像处理中的高内存存储需求。

图像压缩算法

• 利用图像中相邻像素高度相关这一事实，我们可以通过寻找相关度较低的图像表示来丢弃这些冗余的信息，这是图像压缩算法背后的基本理论。下图展示图像编码过程的基本组成，图像编码过程分为两个阶段，图像变换阶段和熵编码阶段。
  

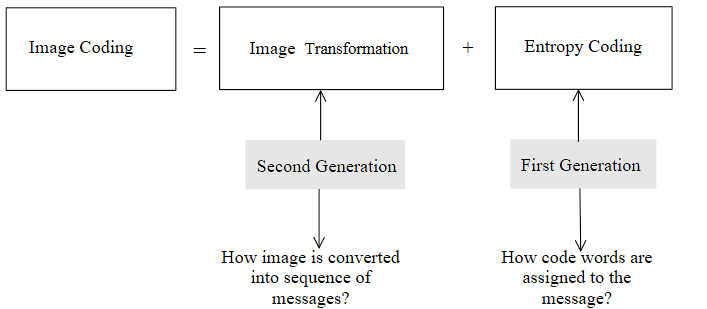
图像编码可分为第一代和第二代：

• 第一代图像编码更强调如何有效地编码转换后的图像所包含的信息

• 第二代图像编码更重视如何从图像中挖掘和提取有用的信息

• 文章在第一代编码中介绍了四种最流行的基于变换的图像压缩算法——JPEG、EZW、SPIHT和EBCOT，其中EZW、SPIHT和EBCOT在上一部分“小波系数图像压缩编码”中已经做了详细的介绍，在此不再展开。

• 著名的图像压缩标准JPEG使用了基于离散余弦变换(DCT)的图像压缩技术，将图像分为多个8 x 8像素的子图像块，并对每个图像块独立编码。DCT不对原始数据造成损失，经过离散余弦变换后，每个64DCT系数被均匀量化。然后在8 x 8图像块中采用锯齿状扫描重新排列系数。下图显示了锯齿状扫描的过程：
  

基于DCT的图像压缩提供了令人满意的压缩效率，并且由于编码是在小的单个图像块上完成的，实现时所需的内存很低。然而，图像块的平铺会导致阻塞工件，从而导致性能下降。

第二代图像编码

金字塔/多分辨率编码(Pyramidal/multiresolution coding)

• 金字塔编码在图像发展的早期阶段就已经被引入，但是由于分层编码的方式与人类视觉系统** (Human Visual Syatem, HVS) 中的神经系统类似，所以将其归为第二代图像编码**。
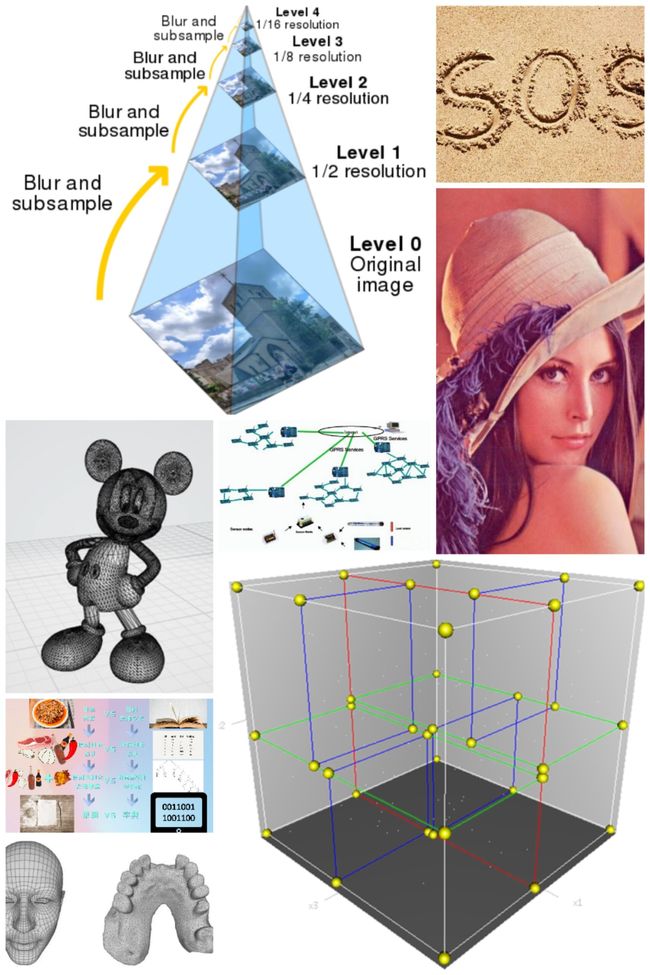
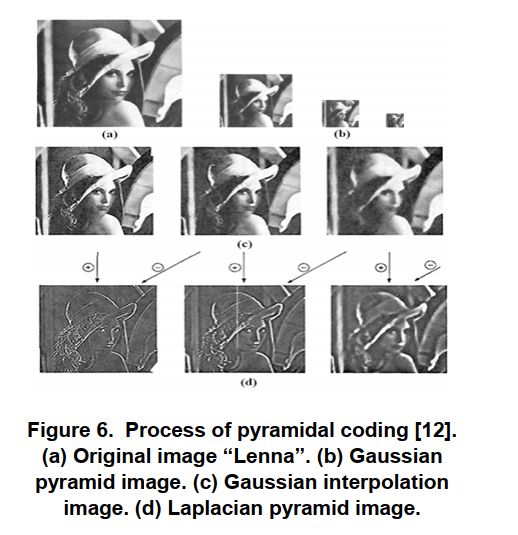
• 通过使用适当的平滑滤镜对图像进行平滑处理，然后对平滑图像进行子采样（通常沿每个坐标方向按 2 倍）来生成低通金字塔。然后，对生成的图像进行相同的过程，并重复多次循环。此过程的每个周期都会导致图像变小，平滑度增加，但空间采样密度降低（即图像分辨率降低）。如果以图形方式进行说明，则整个多尺度表示将看起来像一个金字塔，原始图像位于底部，每个周期生成的较小图像将一个堆叠在另一个之上：
  

上图是金字塔编码的形象化表示。

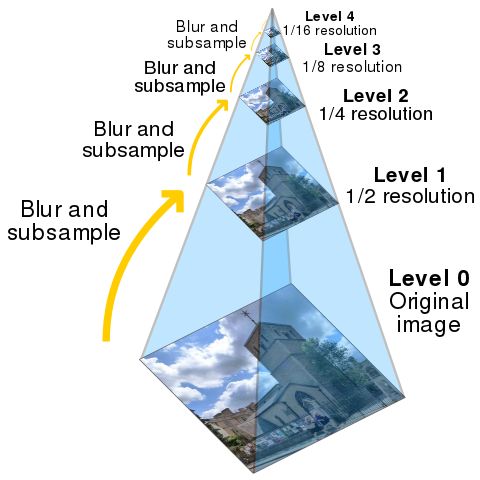
上图为金字塔编码的实例，其中各图分别表示：

1. 原始图像“Lenna”
2. 高斯金字塔图像
3. 高斯插值图像
4. 拉普拉斯金字塔图像

• 高斯核和拉普拉斯核是两种对图像进行平滑处理的核函数。拉普拉斯金字塔算法基于空间频率将图像分解为多个分量，金字塔中每个节点的值代表两类高斯函数与原始图像卷积的差值（平滑处理）。

基于方向分解的编码(Directional decomposition based coding)

• 从对HVS本质的研究和分析中发现，边缘信息在图像的感知中至关重要。然而采用传统的变换编码、子带编码和小波编码等编码方法对图像进行编码时，这些信息往往会发生畸变。定向滤波编码更强调边缘检测，以实现高压缩比。它基于人眼是由对方向敏感的神经元组成的事实，一个方向滤波器用于利用边缘之间的关系及其对图像光谱的贡献。该滤波器被定义为“沿主方向进行高通滤波，沿正交方向进行低通滤波的滤波器”。
• 在方向滤波过程中，将原始图像分解为一副低通图像和若干幅高通图像。每个高通图像都包含一个主方向的边缘信息，因此图像中的边缘信息得到很好的保存(相比于之前提到的传统的变换编码、子带编码和小波编码等编码方法)。低通图像不包含边缘信息，可以采用变换编码，而高通图像采用边缘检测和编码。

基于分割的编码(Segmentation based coding)

• 与基于方向分解的编码类似，该编码利用了人眼善于识别相似区域并将其分组为事实，根据图像的纹理结构将图像划分为子区域。这些子区域被轮廓包围，轮廓和纹理区域将分别进行编码。下图展示了基于分割的编码过程：
  

1. 基于对HVS的特征和分析，首先对图像进行预处理，去除噪声和无用区域。
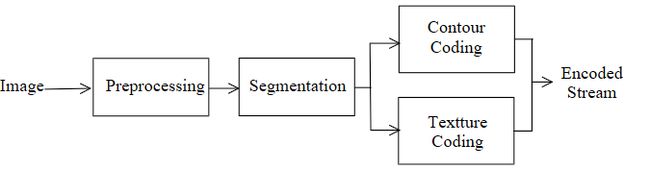
2. 在分割的过程中，采用一种基于区域增长的编码方法，每个像素和它的相邻像素根据灰度级别来判断它们是否共享相同的属性。重复这个区域增长过程，直到所有的像素都被分配某个区域，这样会得到很多子区域。为了减少区域数，降低编码复杂度，会将弱对比即相比差距不大的相邻区域和小区域进行合并。
3. 最后进分别对轮廓区域和纹理区域进行轮廓编码和纹理编码。

矢量量化(Vector quantization)

• 矢量量化，顾名思义就是利用矢量表示图像。利用矢量量化对图像编码时，首先将高度相关的像素分组为样本集的块，每一个块都可以找到一个最佳的近似向量来表示给定区域中的每个像素。对这些像素块进行量化，然后每个块独立编码，基于这个过程，矢量量化又被称为块量化或者模式匹配量化。下图为矢量量化编码的框图：
  

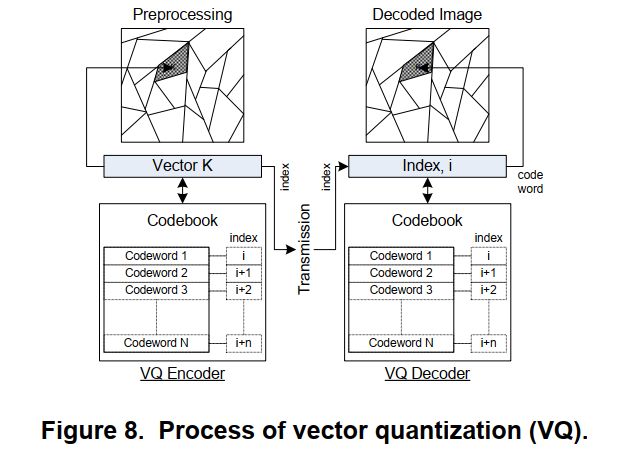
• 编码

1. 图像预处理，将图像分割成像素块
2. 为每个像素块找到一个表示向量k
3. 将向量k与查找表（码本）中预定义的向量集（码字）进行比较，选择最匹配的码字
4. 为了获得更高的压缩比，传输的是码字的索引而不是码字本身，索引比码字本身占用的位数更少。

• 解码

1. 根据接收到的索引值从码本中选取码字
2. 利用码字重构图像

• 从矢量量化编码的过程中我们可以看到，每幅图片可以划分成各种各样的子区域，这些子区域对应的矢量是非常多的，将大量的矢量编码成码本中有限的码字，会造成数据的损失，因此矢量量化提供了有损压缩。

观察和总结

Characteristic	First Generation Image Compression Algorithm				Second Generation Image Compression Algorithm
	JPEG	EZW	SPIHT	EBCOT	Pyramidal	Directional Decomposition	Segmentation	Vector Quantization
Preprocessing(Transformation)	DCT	DWT	DWT	DWT	Laplacian Pyramid	Directional filtering	Region rowing	Region clustering
Coding Table/Codebook	no	no	no	yes	Depends on entropy Coding used		yes	yes
Post processing(Entropy Coding)	Arithmetic Coding	Arithmetic Coding	Not needed	Arithmetic Coding	Entropy Coding	Entropy Coding	Entropy Coding	Entropy Coding
Memory Requirement	Low	Average	Average	High	Average	Average	High	High
Computation Load	Low	Low	Low	High	Average	Average	Extensive	Extensive
System Complexity	Low	Average	Average	High	Low	Average	High	High
Coding Speed	High	High	Average	High	Average	Low	Low
Compression Quality	Low	Average	High	High	Low	Average	High	High
Most sutiable for WSN			√

**表：第一代和第二代图像压缩算法分析总结**

分析与对比

• 上表总结了八种图像压缩算法的特性和特点，并且选择SPIHT为最适合在无线传感器网络中实现的图像压缩算法。选择的标准是所选算法应具备运行在硬件受限的环境下的WSN的大多数首选特征，包括快速高效的图像处理能力、低内存需求、高压缩质量、低系统复杂度和低计算负载。
• 除此之外，我们还可以得出：

1. 第一代图像压缩算法是利用图像像素之间的相似性来消除图像中的冗余，而第二代图像压缩算法结合了HSV的特性，识别图像中的特征，并对这些特征进行处理。第二代图像编码强调探索图像的“内容”，与第一代进行小波变换的图像编码相比，这一特性需要更复杂和更广泛的图像处理。
2. 大多数第二代图像压缩算法提供有损压缩，它们依赖于初始的分割。在分割过程中，首先将图像像素划分为轮廓区域和纹理区域，然后进行区域增长过程。整个图像的预处理过程被存储在内存中，在WSN节点中是很难实现的。此外，分割时所需的大量的计算增加编码器的复杂性并且降低了处理速度，使其在实时环境中不可能实现。

计算机视觉中的女神 —— Lenna

在数字图像处理中，Lena（Lenna）是一张被广泛使用的标准图片，特别在图像压缩的算法研究中。

• 莱娜·瑟德贝里（瑞典文：Lena Soderberg），1951年3月31日出生于瑞典，在1972年11月期的《花花公子》杂志中，她化名为莱娜·舍布洛姆，成为了当期的玩伴女郎。她的中间折页照片由Dwight Hooker拍摄。她的照片（即莱娜图）后来被数字图像处理领域所广泛使用。1997年，在图像科学和技术协会（英语：Society for Imaging Science and Technology）的第50届会议上，她被邀为贵宾出席。在会议上，她忙于签名、拍照以及介绍自我。
  熟悉图像处理或者压缩的工程师、研究人员和学生经常在他们的实验或者项目任务里使用“Lenna”或者“Lena”的图像。Lenna图像已经成为被广泛使用的测试图像。今天，Lenna图像的使用被认为是数字图像历史上最重要的事件之一。然而，很少有人看过原始的图像并知道完整的关于Lenna的故事。

Lenna/Lena是谁？

• 从comp.compression FAQ中， 我们知道Lenna/Lena是一张数字化了的1972年12月份的《花花公子》折页。Lenna这个单词是在《花花公子》里的拼法，Lena是她名字的瑞典语拼法。（在英语中，为了正确发音，Lena有时被拼做Lenna。）关于Lena Soderberg (ne Sjooblom)的报道说她居住在她的本国瑞典，有着幸福的婚姻并是三个孩子的妈妈，在liquor monopoly州有一份工作。1988年，她被某个瑞典计算机相关杂志采访，因为她的照片而发生的一切令她很高兴。这是她第一次得知她的照片在计算机领域被使用。

为何要使用Lenna图像？

• David C. Munson. 在“A Note on Lena” 中给出了两条理由：首先，Lenna图像包含了各种细节、平滑区域、阴影和纹理，这些对测试各种图像处理算法很有用。它是一副很好的测试图像！第二，Lena图像里是一个很迷人的女子。所以不必奇怪图像处理领域里的人（大部分为男性）被一副迷人的图像吸引。

谁制作了Lenna图像？

• 在1999年10月29日，一封来自Chuck McNanis的email，里面告诉我们这个曾经扫描了Lenna图像的“不知名的科研人员”是William K. Pratt博士。下面是email：
  我在图像处理研究所的图像处理实验室作为一个系统程序员工作了5年（'78-'83），这个实验室发布了Lenna图像和其他一些被人们经常引用做“The baboon image”的图像（包括Manril）。这个“不知名的科研人员”是William K. Pratt博士，在Sun Microsystems。他当时正在写一本关于图像处理的书，他需要几张标准图像。很长一段时间以来，折叠的折叠式折叠式折页一直放在实验室的文件柜中。1997年我回去参观时，实验室发生了许多变化，原来的图像文件找不到了。最初的分发格式是1600BPI的9轨磁带，每个色板单独存储。–Chuck McManis (USC Class of '83)

原始图像编辑

• 标准的数字Lena图像只是原始图像的脸和露肩特写。曾在Chuck Rosenberg获得了原始的《花花公子》杂志的图像，并把它放在网上。
  

现在的Lenna

• Lena女士居住在瑞典，并且已经是3个小孩的母亲，过着快乐的生活。1997年，Lena被邀请参加了第50届IS&T会议。
  

无线传感器网络数据压缩

• 近年来，随着电子设备的不断发展，大家可能都意识到了自己身边都多了一些可以联网的智能电子设备，智慧农业，智慧交通等也不断地发展，应用到相应地场景中；有关无线传感器网络的研究也越来越多，越来越多的人也逐渐意识到无线传感器网络的无限适用性。例如，传感器网络可用于环境监测、生境检测、结构检测、设备诊断、灾害管理和应急响应等情况下收集数据。
  但是无线传感器网络（WSNs）在应用的时候有一些资源的限制：有限的电源供应、通信带宽、处理速度和内存空间。最大限度地利用这些资源的一种可能的方法是对传感器的数据进行数据压缩。
• ++通常情况下，处理数据比在无线介质中传输数据消耗的能量要少很多，因此在传输数据前采用数据压缩可以有效的降低传感器节点的总功耗。++然而，现有的大部分压缩算法对于处理能力非常弱的传感器节点实在是过于庞大，以及每个传感器节点都受到了电力等资源的限制。所以，怎么在传感器节点这种资源限制非常大的情况下并设计我们的压缩算法是最主要的问题。
  

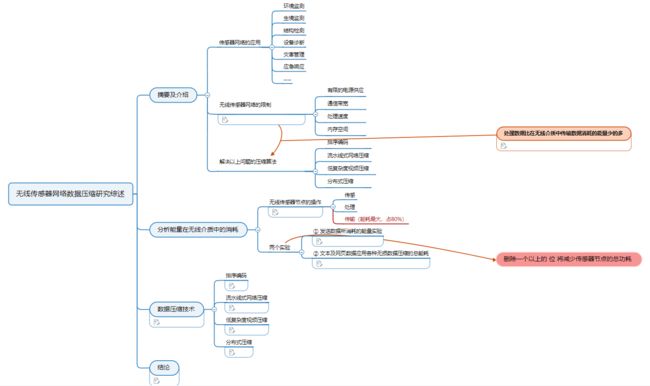
分析能量在无线介质中的能量消耗

• 从功耗上看，无线传感器节点的运行可分为 传感、处理和传输三部分。在这三种操作中，已知能耗最大的任务是数据传输。++每个传感器节点约 80% 的功耗用于数据传输。++
  因此，如果我们能通过数据压缩使数据的大小最小化，就会减少传输功率。然而，另一方面，通过数据压缩，将需要更强大的处理能力来执行压缩算法。为了减少的总功耗，必须减少传输和处理的总功耗。将 “a” 位的数据字符串压缩为 “b” 位的数据字符串所消耗的功耗，其中 a>b 。

实验① 发送数据所消耗的能量实验

• 这个实验室通过执行一个简单的32位加法指令，发送1位来采集功耗数据。
• 结果表明，发送 1个 bit 的数据大约消耗 0.4µJ 的能量，执行一条加法指令只想消耗 0.86nJ 的能量。通过无线电媒体传输一个 bit 的功耗至少是执行一个额外指令的 480倍。
  所以如果通过压缩操作从原始数据位串中删除一个以上的位（相当于 480条 加法指令），将减少传感器节点的总功耗。

实验② 文本及网页数据应用各种无损数据压缩的总功耗

• 这个实验测试的压缩算法有 bzip2 (BWT 算法), compress (LZE 算法), LZO (LZ77), PPMd (PPM) 和 zlib (LZ77).
• 实验结果表明，对于大多数压缩算法，在传输数据前压缩数据可以减少总功耗。然而在某些情况下，应用数据压缩会增加总功耗，这是由于在压缩执行期间访问内存。访问内存在能量消耗方面是昂贵的。

结论：

• 在无线介质中传输数据前采用数据压缩是降低能耗的有效方法。然而，选择一种数据压缩算法是至关重要的，它在执行期间需要较少的内存访问。

数据压缩技术

① 排序编码

作为数据漏斗路由的一部分，引入了按顺序编码的数据压缩方案。压缩方案如下：

1. 将数据从感兴趣区域（Interested region）中的传感器节点传递到收集器节点，如图一所示。在数据漏斗路由中，一些传感器节点作为数据汇聚节点工作。
   例如:节点 A、节点 B、节点 D 为数据汇聚节点。在汇聚节点上，将其他节点收集到的传感数据进行组合，并将聚合后的数据发送给其父节点。在图 3 的节点 D 处，节点 E 收集的数据与节点 D 本身收集的数据相结合。
2. 然后，将聚合的数据传输到节点 B
   

结论：

1. 该数据压缩方法压缩比比较低，算法简单，有可能应用在无线传感器网络上。
2. 使用该方案的一个困难是，由于没有有效的算法将排列映射到数据值，因此它需要一个映射表。随着聚集的传感器节点的增加，表的大小呈指数增长。

② 流水线式网络压缩

这里讨论了流水线式网络压缩方案。其基本思想是用高数据传输延迟换取低传输能耗。收集到的传感器数据在聚合节点的缓冲区中存储一段时间。在此期间，将数据包合并成一个数据包，消除数据包中的冗余，使数据传输最小化。

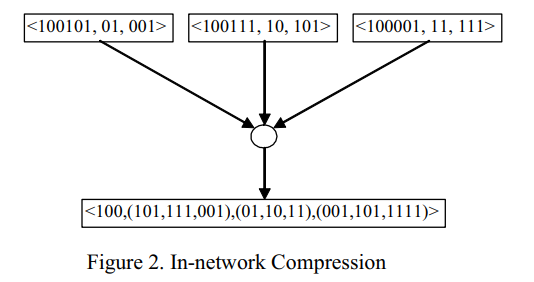
结论：

• 优点：
  这种简单压缩方案的一个优点是，可以将共享前缀系统用于节点 id 和时间戳。通过这样做，可以实现更多的数据压缩。
  数据压缩的效率取决于共享前缀的长度。如果我们可以设置一个很长的共享前缀，并且测量值具有共性，压缩比就会增加。
• 缺陷：
  然而，测量的传感器值没有相似之处。即使设置一个很长的共享前缀，也会降低网络内流水线压缩的效率。
  此外，如果我们要合并大量的数据包，那么就需要一个大的数据缓冲区来临时存储这些数据包。由于传感器节点的内存空间有限，因此没有足够的缓冲区空间可用。

③ 低复杂度视频压缩

这里引入了低复杂度的视频压缩方案。由于目前的视频编码技术大多是利用运动估计和补偿来设计的，因此需要较高的计算能力，而传感器节点通常不具备这种能力。因此，该方法是基于块变化检测算法和 JPEG 数据压缩的。

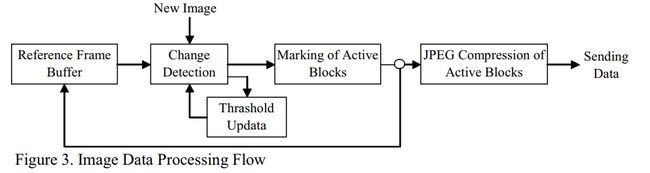
上图给出了图像数据处理流程的框图。该算法是专门针对无线视频监控系统而设计的。该方法将每个视频帧划分为小块，每个块包含 8 个 8(64)像素。为了降低计算复杂度，在每一帧中只考虑块的子集(本例中为所有的白色块)。此外，在每个块中，将检查像素子集(分配的像素数目)的变化，如图 7 所示。分配给像素的数字表示像素的重要性(1 =最重要，3 =最不重要)。

结论：

• 实验结果表明，该算法处理后的图像质量与MPEG-2 处理后的图像质量相当，同时实现了一定的节能。

④ 分布式压缩

分布式压缩方案背后的基本思想是使用一个边信息来编码一个源信息。然后，解码器在陪集中选择一个与 Y 发送的码向量值最接近的码向量。

结论：

• 分布式压缩方案不仅可以应用于如上述例子所示的离散源，也可以应用于连续源。此外，它可以用于无损和有损压缩方案。

总结

• 近年来，人们对无线传感器网络的应用领域进行了广泛的讨论。未来随着技术的发展，无线传感器网络的应用领域将比现在更加广泛。人们将比现在更容易得到它们。然而，在这些日子到来之际，传感器网络的实际应用仍然存在许多障碍需要克服。其中一个障碍是无线节点资源有限。
• 本文已处理5种不同类型的数据压缩方案：排序编码、流水线网络压缩、JPEG200、低复杂度视频压缩和分布式压缩。尽管这些压缩方案仍处于开发阶段，但实验结果表明，它们的压缩率和功率降低方式相当令人深刻。它们是无线传感器节点资源约束的一种可行方法。

参考文献

[1] Vitter, Scott J . Design and analysis of dynamic Huffman codes[J]. Journal of the Acm, 1987, 34(4):825-845.
[2] Peng J , Kim C S , Kuo C C J . Technologies for 3D mesh compression: A survey[J]. Journal of Visual Communication & Image Representation, 2005, 16(6):688-733.
[3] Holtz K . The evolution of lossless data compression techniques[C]// Wescon/93 Conference Record. IEEE, 1993.
[4] Kimura N , Latifi S . A survey on data compression in wireless sensor networks[C]// International Conference on Information Technology: Coding and Computing (ITCC’05) - Volume II. IEEE, 2005.
[5] Sudhakar R , Karthiga M R , Jayaraman S . Image compression using coding of wavelet coefficients–a survey[J]. A Survey”, ICGST-GVIP Journal, Volume (5), Issue, 2005(6):25-38.
[6] Li W C , Ang L M , Seng K P . Survey of image compression algorithms in wireless sensor networks[C]// International Symposium on Information Technology. 2008.
[7] Hamming R W . Coding and information theory (2. ed.)[M]. DBLP, 1986.
[8] 高锐智, 华成英. 汉字字形结构式压缩方法的研究和实现[J]. 计算机科学, 2003, 30(005):78-81.
[9] Zhang C N , Wu X . A hybrid approach of wavelet packet and directional decomposition for image compression[J]. Wiley Subscription Services, Inc. A Wiley Company, 2002, 12(2):51-55.
[10] Kunt, M, Ikonomopoulos, et al. Second-generation image-coding techniques[J]. Proceedings of the IEEE, 1985.