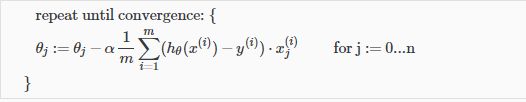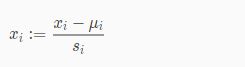机器学习笔记 | multivariate linear regression（多元线性回归）

设置编程环境

Octave是一个自由的，开放源码可以在许多平台的应用。它有一个文本界面和实验的图形之一。

MATLAB是专有软件，但免费的试用许可到MATLAB在线注册账户。

MATLAB在线：https://matlab.mathworks.com/

在windows安装Octave： http://wiki.octave.org/Octave_for_Microsoft_Windows（不要安装4.0.0版本）

更多Octave文档：https://octave.org/doc/interpreter/

1、多特性（Multiple Features）

线性回归与多个变量也称为“多元线性回归（multivariate linear regression）”。

多元变量下的假设形式：

使用矩阵乘法的定义，我们的多变量假设函数可以简明地表示为:

为了方便，我们假设x (i) 0 = 1 (∈1,…, m)。这方便我们做矩阵运算。

2、多个变量下的梯度下降（Gradient Descent for Multiple Variables）：

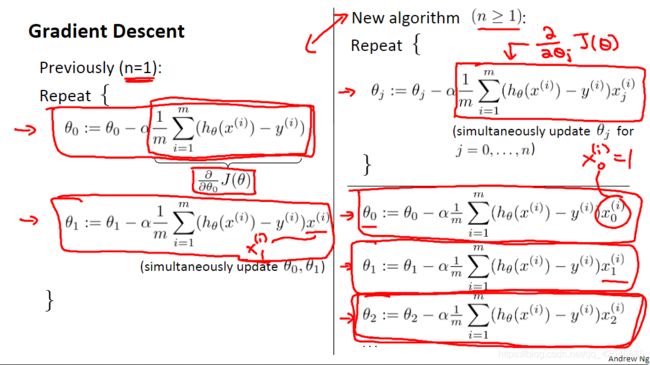
梯度下降方程一般是相同的形式，只需要重复我们的“n”功能:

梯度下降法一个变量与多个变量：

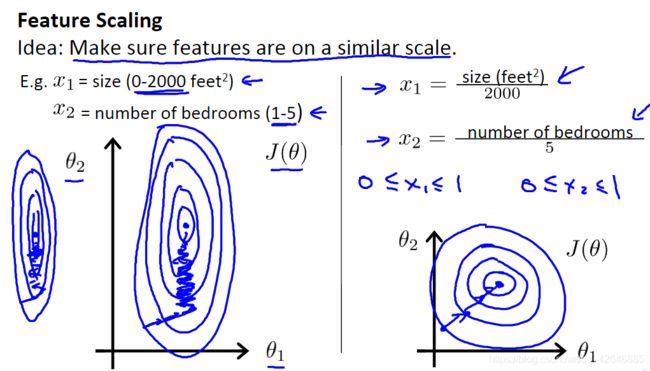
3、梯度下降在实践I -特征缩放（Feature Scaling）：

可以通过修改输入变量的范围，加快梯度下降。理想情况是：

−1 ≤ x(i)​ ≤ 1

or

−0.5 ≤ x(i)​ ≤ 0.5

这些不是确切的要求;我们只是试图加快速度。我们的目标是让所有输入变量大致进入其中一个范围，或多或少。

 

有两种技术可以帮助解决这个问题，一种是特性缩放（feature scaling），另一种是均值标准化（ mean normalization）。

特征缩放是将输入值除以输入变量的范围(即最大值减去最小值)，得到的新范围只有1。

均值标准化涉及到从输入变量的值中减去输入变量的平均值，从而得到输入变量的新平均值为零。

μ1：在训练集中特征 x(i )的平均值

S1： 该特征值的范围 ，即最大值减去最小值 

 

4、梯度下降法在实践中II -学习速率（Learning Rate）：

梯度下降算法所做的事情 ，就是找到 一个 θ 值 并希望它能够最小化代价函数 J(θ) 。

调试梯度下降，在x轴上画一个迭代次数较多的图。纵轴是代价函数，表示J(θ)梯度下降法的迭代次数。如果J(θ)的增加,那么可能需要降低α。

总结：

学习速率α足够小（适当）：那么J(θ)将在每次迭代减小。

如果α太小：收敛速度慢。

 如果α太大:：可能不会在每次迭代减少,因此可能不收敛。

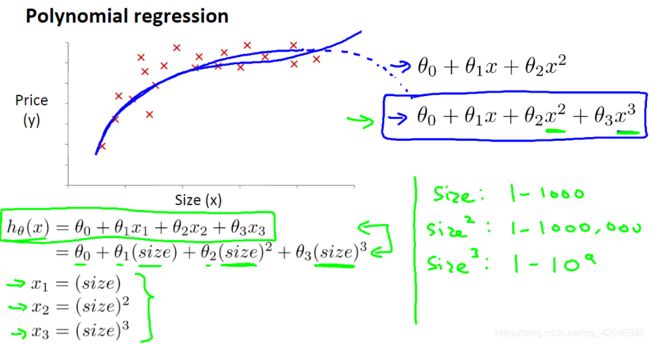
5、特性和多项式回归（Features and Polynomial Regression）：

我们可以用几种不同的方法来改进我们的特征和假设函数的形式。

可以将多个特性组合成一个。例如，我们可以组合x(1) 和x (2) 变成一个新特性x(3). 通过x(1) * x(2) .

如果我们的假设函数与数据不匹配，那么它就不需要是线性的(一条直线)。可以通过将假设函数变成二次函数、三次函数或平方根函数(或任何其他形式)来改变其行为或曲线。

如果假设函数是

可以基于x(1)创建其他特性，得到二次函数

或者三次函数

注意特征值的范围大小也随之改变。 如果使用梯度下降法，应用特征值的归一化是非常重要的，这样才能将他们的值的范围变得具有可比性。就是将他们的范围缩小在相差不多的范围区间。

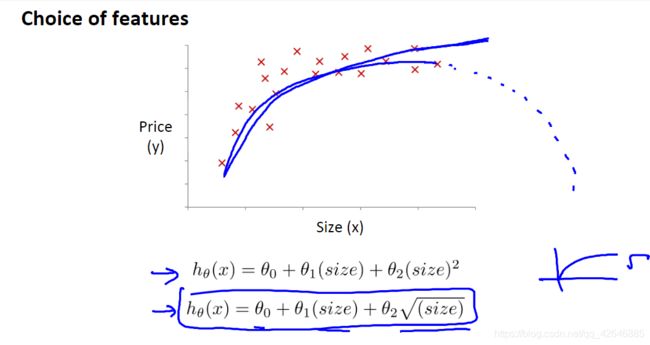
本节学习目的：需要选择使用什么特征并且通过设计不同的特征，能够用更复杂的函数去拟合数据 。而不是只用 一条直线去拟合，可以使用多项式函数。另外需要通过采取适当的角度来观察特征来得到一个更符合你的数据的模型 。