【模式识别】隐马尔可夫模型(HMM)
隐马尔可夫模型(HMM)
-
-
- 引言
- HMM模型定义
-
- 模型
- 两个假设
- HMM解决的三个基本问题
-
- 1、Evaluation问题
- 2、Learning问题
- 3、Decoding问题
- Evaluation问题求解(前向算法和后向算法)
-
- 前向算法
-
- 算法推导
- 算法流程
- 后向算法
-
- 算法推导
- 算法流程
- Learning问题(EM算法求解)
-
- EM算法求解
- Decoding问题(EM算法求解)
-
引言
机器学习领域分为两个流派:频率派和贝叶斯派。频率派逐渐发展为统计机器学习学科,其核心问题为优化问题。定义出定义一个模型,计算损失函数,再通过随机梯度下降、牛顿拟牛顿法等最优化方法进行求解。贝叶斯派发展出概率图模型,最终解决的是推断问题,通过计算后验概率,使用数值积分、蒙特卡罗方法等方法进行求解。
本文中的HMM方法即是一种概率图模型,而且是一种无向概率图模型。隐马尔可夫模型(Hidden Markov Model,HMM),是一种可用于标注问题的统计学习模型,其最早在NLP领域大放异彩,可以用于语音识别、机器翻译,并在上世纪八十年代开始被应用于生物信息领域。
HMM模型定义
一个标准的马尔可夫过程中,状态对于观察者来说都是可见的,由此通过初始分布以及状态转移概率便可以完全确定一个马尔可夫过程(参见《随机过程》,马尔可夫过程部分),由此衍生出来的隐马尔可夫模型,描述的是由隐藏的马尔科夫链随机生成不可观测的状态序列,再由每个状态生成随机的可观测序列的过程,属于生成模型。
模型
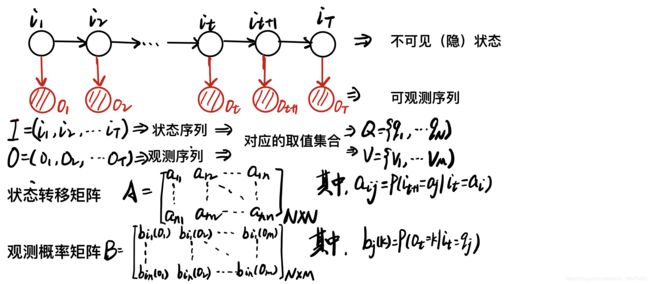
即:马尔可夫链 → 状态序列(不可观测)→观测序列(可观测),由下图直观显示:
一个隐马尔科夫模型可以由初始概率分布 、状态转移概率分布、观测概率分布确定。
初始概率分布指的是初始状态的概率向量 π \pi π,状态转移概率分布指的是状态转移矩阵A,观测概率分布指的是观测概率矩阵B。其中, π \pi π和A确定了隐藏的马尔可夫链,生成不可观测状态序列。B和状态序列则确定了如何产生观测序列。所以隐马尔科夫模型 λ \lambda λ可以用三元符号表示:
λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)
两个假设
同时,隐马尔可夫模型需要满足两个假设:
(a)马尔可夫性(无后效性):下一个时刻的状态至于当前时刻状态有关,与之前所有时刻均无关;
(b)观测独立性:同一时刻的观测只与当前时刻的状态相关,与其它观测和状态均无关。
HMM解决的三个基本问题
1、Evaluation问题
即概率计算问题,给定模型λ和观测序列O,计算在模型λ下模型O出现的概率P(O|λ);
解决方法:前向算法和后向算法。
2、Learning问题
已知观测序列O,估计模型λ;
解决方法:EM算法,参见:【模式识别】期望最大化算法(EM算法)。
3、Decoding问题
即预测问题,给定观测序列O,求最有可能的对应的状态序列。即已知λ和O,求I = argmaxP(I|O)。
进而引申出两个问题:
(a).预测问题:求 p ( i t + 1 ∣ o 1 , . . . , o t ) p(i_{t+1}|o_1,...,o_t) p(it+1∣o1,...,ot)
(b).滤波问题:求 p ( i t ∣ o 1 , . . . , o t ) p(i_t|o_1,...,o_t) p(it∣o1,...,ot)
Evaluation问题求解(前向算法和后向算法)
输入:模型λ和观测序列O
输出:P(O|λ)
根据概率论中的基本定理,我们有:
P ( O ∣ λ ) = ∑ I P ( O , I ∣ λ ) = ∑ I P ( O ∣ I , λ ) P ( I ∣ λ ) P(O|\lambda)=\sum_IP(O,I|\lambda)=\sum_IP(O|I,\lambda)P(I|\lambda) P(O∣λ)=I∑P(O,I∣λ)=I∑P(O∣I,λ)P(I∣λ)
其中:
p ( I ∣ λ ) = p ( i 1 , i 2 , ⋯ , i t ∣ λ ) = p ( i t ∣ i 1 , i 2 , ⋯ , i t − 1 , λ ) p ( i 1 , i 2 , ⋯ , i t − 1 ∣ λ ) p(I|\lambda)=p(i_1,i_2,\cdots,i_t|\lambda)=p(i_t|i_1,i_2,\cdots,i_{t-1},\lambda)p(i_1,i_2,\cdots,i_{t-1}|\lambda) p(I∣λ)=p(i1,i2,⋯,it∣λ)=p(it∣i1,i2,⋯,it−1,λ)p(i1,i2,⋯,it−1∣λ)
根据齐次 Markov 假设: p ( i t ∣ i 1 , i 2 , ⋯ , i t − 1 , λ ) = p ( i t ∣ i t − 1 ) = a i t − 1 i t p(i_t|i_1,i_2,\cdots,i_{t-1},\lambda)=p(i_t|i_{t-1})=a_{i_{t-1}i_t} p(it∣i1,i2,⋯,it−1,λ)=p(it∣it−1)=ait−1it 所以: p ( I ∣ λ ) = π 1 ∏ t = 2 T a i t − 1 , i t p(I|\lambda)=\pi_1\prod\limits_{t=2}^Ta_{i_{t-1},i_t} p(I∣λ)=π1t=2∏Tait−1,it 又由于: p ( O ∣ I , λ ) = ∏ t = 1 T b i t ( o t ) p(O|I,\lambda)=\prod\limits_{t=1}^Tb_{i_t}(o_t) p(O∣I,λ)=t=1∏Tbit(ot) 于是: p ( O ∣ λ ) = ∑ I π i 1 ∏ t = 2 T a i t − 1 , i t ∏ t = 1 T b i t ( o t ) p(O|\lambda)=\sum\limits_{I}\pi_{i_1}\prod\limits_{t=2}^Ta_{i_{t-1},i_t}\prod\limits_{t=1}^Tb_{i_t}(o_t) p(O∣λ)=I∑πi1t=2∏Tait−1,itt=1∏Tbit(ot) 我们看到,上面的式子中的求和符号是对所有的观测变量求和,于是复杂度为 O ( T N T ) O(TN^T) O(TNT),可知此方法计算量极大,下面介绍有效算法,前向-后效算法。
前向算法
算法推导
首先给出前向概率定义:给定隐马尔可夫模型λ和O,将t时刻的 i t i_t it以及到t时刻为止的所有观测序列的联合概率密度记为 α t ( i ) \alpha_t(i) αt(i)(表达式如图)则T时刻有 α T ( i ) \alpha_T(i) αT(i),所以我们可以用 α T ( i ) \alpha_T(i) αT(i)将要求的P(O|λ)表达出来。此文问题从解P(O|λ)变为解 α T ( i ) \alpha_T(i) αT(i),我们希望能发现 α t ( i ) \alpha_t(i) αt(i)和 α t + 1 ( j ) \alpha_{t+1(j)} αt+1(j)的关系,之后即可通过递推的方法求得最后时刻的 α T ( i ) \alpha_T(i) αT(i),具体推导如图。

算法流程
所以我们就得到了前向算法:
输入:隐马尔可夫模型λ,观测序列O
输出:观测序列概率P(O|λ)
a.初值: α 1 ( i ) = π i b i ( o 1 ) \alpha_1(i)=\pi_ib_i(o_1) α1(i)=πibi(o1), $ i=1,2,…,N$
b.递推:对于t=1,2,…,T-1
α t + 1 ( i ) = ∑ j = 1 N α t ( j ) a j i b i ( o t + 1 ) , 其 中 i = 1 , 2 , 3 , . . . , N \alpha_{t+1}(i)=\sum_{j=1}^N\alpha_t(j)a_{ji}b_i(o_{t+1}),其中i=1,2,3,...,N αt+1(i)=j=1∑Nαt(j)ajibi(ot+1),其中i=1,2,3,...,N
c.终止:
P ( O ∣ λ ) = ∑ i = 1 N α T ( i ) P(O|\lambda)=\sum^N_{i=1}\alpha_T(i) P(O∣λ)=i=1∑NαT(i)
后向算法
算法推导
后向算法与前向算法类似,它通过定义后向传播概率 β t ( i ) \beta_t(i) βt(i)从后往前实现递推过程得到 β 1 ( i ) \beta_1(i) β1(i),并使用 β 1 ( i ) \beta_1(i) β1(i)表示出P(O|λ),内容如下图
算法流程
输入:隐马尔可夫模型λ,观测序列O
输出:观测序列概率P(O|λ)
a.初值: β t ( i ) = 1 \beta_t(i)=1 βt(i)=1, $ i=1,2,…,N$
b.递推:对于t=1,2,…,T-1
β t ( i ) = ∑ j = 1 N a i j b j ( o t + 1 ) β t + 1 ( j ) , 其 中 i = 1 , 2 , 3 , . . . , N \beta_{t}(i)=\sum_{j=1}^Na_{ij}b_j(o_{t+1})\beta_{t+1}(j),其中i=1,2,3,...,N βt(i)=j=1∑Naijbj(ot+1)βt+1(j),其中i=1,2,3,...,N
c.终止:
P ( O ∣ λ ) = ∑ i = 1 N π i b i ( o 1 ) β 1 ( i ) P(O|\lambda)=\sum^N_{i=1}\pi_ib_i(o_1)\beta_1(i) P(O∣λ)=i=1∑Nπibi(o1)β1(i)
前向和后向传播算法复杂度都大大缩减。
Learning问题(EM算法求解)
输入:观测数据 O = ( o 1 , . . . o T ) O=(o_1,...o_T) O=(o1,...oT)
输出:隐马尔可夫模型参数 λ = ( π , A , B ) \lambda=(\pi,A,B) λ=(π,A,B)
EM算法求解
很明显这是一个含有隐变量的概率模型,故可以使用EM算法求解:
1:在 MLE 中,完全数据的对数似然函数为: l n P ( O , I ∣ λ ) ln P(O,I|\lambda) lnP(O,I∣λ)
2:EM算法:Q函数为
Q ( λ , λ ( t ) ) = ∑ I log P ( O , I ∣ λ ) p ( O , I ∣ λ t ) = ∑ I [ log π i 1 + ∑ t = 2 T log a i t − 1 , i t + ∑ t = 1 T log b i t ( o t ) ] p ( O , I ∣ λ t ) Q(\lambda,\lambda^{(t)})= \sum\limits_I\log P(O,I|\lambda)p(O,I|\lambda^t)=\sum\limits_I[\log \pi_{i_1}+\sum\limits_{t=2}^T\log a_{i_{t-1},i_t}+\sum\limits_{t=1}^T\log b_{i_t}(o_t)]p(O,I|\lambda^t) Q(λ,λ(t))=I∑logP(O,I∣λ)p(O,I∣λt)=I∑[logπi1+t=2∑Tlogait−1,it+t=1∑Tlogbit(ot)]p(O,I∣λt)
对 π t + 1 \pi^{t+1} πt+1:
π t + 1 = arg max π ∑ I log π i 1 P ( O , I ∣ λ t ) \pi^{t+1}=\arg\max_{\pi} \sum_I\log \pi_{i_1}P(O,I|\lambda^t) πt+1=argπmaxI∑logπi1P(O,I∣λt)
上面的式子中,对 i 2 , i 2 , ⋯ , i T i_2,i_2,\cdots,i_T i2,i2,⋯,iT 求和可以将这些参数消掉: π t + 1 = a r g m a x π ∑ i 1 [ log π i 1 ⋅ p ( O , i 1 ∣ λ t ) ] \pi^{t+1}=\mathop{argmax}_\pi \sum\limits_{i_1}[\log \pi_{i_1}\cdot p(O,i_1|\lambda^t)] πt+1=argmaxπi1∑[logπi1⋅p(O,i1∣λt)] 上面的式子还有对 π \pi π 的约束 ∑ i π i = 1 \sum\limits_i\pi_i=1 i∑πi=1。定义 Lagrange 函数: L ( π , η ) = ∑ i = 1 N log π i ⋅ p ( O , i 1 = q i ∣ λ t ) + η ( ∑ i = 1 N π i − 1 ) L(\pi,\eta)=\sum\limits_{i=1}^N\log \pi_i\cdot p(O,i_1=q_i|\lambda^t)+\eta(\sum\limits_{i=1}^N\pi_i-1) L(π,η)=i=1∑Nlogπi⋅p(O,i1=qi∣λt)+η(i=1∑Nπi−1) 于是: ∂ L ∂ π i = 1 π i p ( O , i 1 = q i ∣ λ t ) + η = 0 \frac{\partial L}{\partial\pi_i}=\frac{1}{\pi_i}p(O,i_1=q_i|\lambda^t)+\eta=0 ∂πi∂L=πi1p(O,i1=qi∣λt)+η=0 对上式求和: ∑ i = 1 N p ( O , i 1 = q i ∣ λ t ) + π i η = 0 ⇒ η = − p ( O ∣ λ t ) \sum\limits_{i=1}^Np(O,i_1=q_i|\lambda^t)+\pi_i\eta=0\Rightarrow\eta=-p(O|\lambda^t) i=1∑Np(O,i1=qi∣λt)+πiη=0⇒η=−p(O∣λt) 所以: π i t + 1 = p ( O , i 1 = q i ∣ λ t ) p ( O ∣ λ t ) \pi_i^{t+1}=\frac{p(O,i_1=q_i|\lambda^t)}{p(O|\lambda^t)} πit+1=p(O∣λt)p(O,i1=qi∣λt)
同理可得 a i j a_{ij} aij,以及 b j ( k ) b_j(k) bj(k)
Decoding问题(EM算法求解)
近似算法
维比特算法:动态规划解隐马尔可夫模型预测问题