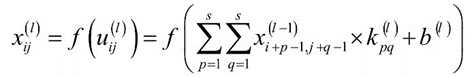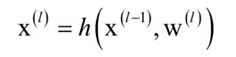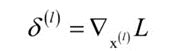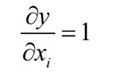简单的神经网络运算框架的实现

摘要：本汇报为简单神经网络运算框架的理论说明。首先在整体性介绍中明确了框架的基本组成部分。通过各层输入数据与训练参数的运算过程描述了前向传播的进行，其中卷积层的前向传播采用矩阵乘法实现，需要对输入数据进行img2col预处理。反向传播部分为框架的难点，汇报从损失函数对各训练参数的梯度计算和各层误差项传递两方面进行说明，其中关键部分的代码实现也给出了具体说明。测试代码中随机生成了batch_size为32的3通道28*28图像数据并搭建了LeNet网络，网络的收敛最终证明了框架的可用性。代码效率分析部分，从运算逻辑和运算性能两方面给出了本框架所做的努力。最后的深入思考，是自己对运算较为复杂的卷积层误差项传递的矩阵乘法实现所做的合理猜想。

关键词：前向传播；误差项传递；梯度计算；img2col；矩阵乘法；numpy

一 整体性介绍

       要实现一个简单的神经网络框架，首先要明确框架最基本的组成要求——各种layer、损失函数的类实现，优化函数的实现，并为这些文件添加__init__.py文件将其变为一个package，关键组成部分实现后应附带测试代码以确保其正确性，进而保证框架的整体的可靠性。同时，为了更方便、更清新的完成上述实现，我还打算编写utils文件（工具包）统一实现涉及到的模块化代码。最后，通过整体测试代码（尽量使用框架的所有组成部分）检验框架的可用性。

       具体结合我自己编写的代码，package为deep目录，包含了线性层、卷积层、池化层、激活层、损失函数及utils文件，每个层的文件中为实现该层的类，包含初始化init和前向传播forward、梯度计算calc_gradient、参数更新forward函数。

二 前向传播

1.全连接层

       全连接层是一种线性运算，主要用作网络的分类器。

其中，W（out, in）与x（in）’之间为矩阵乘法，out为输出神经元的个数，in为输入

神经元的个数，b的shape为（out，1）。

2.卷积层

       卷积层需要明确几个重要的概念——filter（立方体）、kernel（正方形）、stride、

feature_map，同时要时刻清楚的知道卷积层输入、输出图像的通道数（也就是feature_map数）in_channel和out_channel。无论是在前向传播还是反向传播，这几个参数都是十分关键的，同时也是程序编写时的核心参数。

       有了这几个概念后，就是filter与输入图像的计算过程，卷积层进行的也是线性计算，前向传播过程也就是filter和输入图像特定位置的相乘求和，当一个filter和输入图像滑动（涉及stride）计算完成之后，需要加上偏置项。out_channel个filter和输入图像计算完成之后得到out_channel张特征图（feature_map），后面经过pooling和激活可以作为下一个卷积层的输入。

       在代码实现的时候，也就是卷积的具体计算时，通常化卷积运算为矩阵乘法。这需要对输入图像进行img2col的预处理。下面说明img2col的过程：

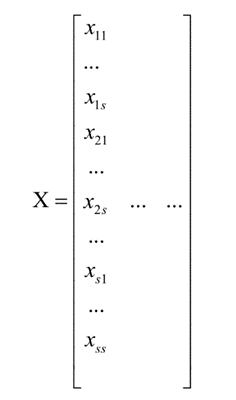
       假设有一个m*n的输入图像

        对于第一个卷积位置的s*s子图像，转换为列向量之后变为：

        对于单通道图像，将所有位置的子矩阵都像这样转换为列向量，最后将nconv个列向量组成矩阵，矩阵的行数为s*s，列数为nconv：

        对于多通道图像，还要将上面的集中单通道图像转换成的矩阵在垂直方向依次拼接起来。最后形成的矩阵的行数为c*s*s，其中c是图像的通道数。

       输入图像的矩阵化较为复杂，在代码实现时，为此过程编写了img2col函数（在utils文件中），每次卷积层前向传播时调用。

       接下来，将卷积核矩阵也转换成向量。具体做法是，将卷积核矩阵的所有行拼接起来形成一个行向量。每个卷积形成一个行向量，有nkernel个卷积核，就有nkernel个行向量。如果卷积核有多个通道，就将这多个通道拼接起来，形成一个更大的行向量。由于卷积层有多个卷积核，因此这样的行向量有多个，将这些行向量合并在一起，形成一个矩阵K。

       filter的矩阵化表示在代码实现时较为简单，直接reshape就可以完成。

       有了输入图像和out_channel个filter的矩阵化表示X和K，卷积层的前向过程就可以表示为KX。

3.池化层

       池化层作为一种非线性层，其前向传播也较为简单，且池化层不含训练参数，因此在反

向传播时只需要将误差项传递到前一层，无需要进行参数更新。

       池化运算主要包括average_pooling和max_pooling两种。分别取feature_map在滑动窗口（涉及stride）内的平均值和最大值。

       本框架实现了max_pooling，需要注意的一点是，为了反向传播时将误差项传递到前一层，max_pooling在前向传播时，需要记录滑动窗口中最大值的位置，该部分会在反向传播中具体解释。

4.激活层及损失函数

       本框架的激活层包含了relu函数和softmax函数，其中softmax函数和cross_entropy

损失函数关系比较密切，因此在loss文件中实现。

relu函数：

 softmax函数：

        其中x为输入数据，f（x）为经过激活后的输出数据。可见激活层完成的都是element-wise运算，反向传播也是如此。因此在代码实现时，无论是前向传播还是反向传播时的误差项传递，经过激活层时，数据的shape都不发生变化，这是激活层的一个特征。

       cross_entropy损失函数描述了预测结果与真实标签之间的分布差异。

        其中x即为softmax激活函数的输出数据，y为样本的真实标签值（ground_truth）。y已经过one_hot编码（对标签值的one_hot编码程序也实现在utils文件中）。

       softmax和cross_entropy的关系较为紧密。因为在进行激活计算时，考虑到数值稳定性，经常使用logsoftmax激活函数，即先取对数后再进行指数运算。这样一来，cross_entropy的计算只需要进行logsoftmax输出和one_hot编码后标签值的element-wise运算再加“-”号即可。one_hot编码后的标签值仅有一位为“1”，其余都为“0”，因此cross_entropy实际上可以表示为：

       其中xj表示与标签值对应的softmax输出。这种简单的表示，对后面误差项的传递也是十分有利的。

三 各层的实现——梯度计算与误差项传递（难点）

       反向传播过程是本框架实现的难点，该部分涉及较多的数学公式推导。主要分为两个子任务——误差损失对训练参数梯度的计算和误差项传递。其中，误差项的传递是为了服务于前一层梯度的计算，而计算出的梯度则用于参数的更新，进而完成网络的训练。具体来说，误差项的计算是一个递归的过程，递归的起点在输出层（损失值对softmax输出值的梯度）。该部分梯度计算和误差传递实现在各层的calc_gradient函数中，参数更新实现在backward函数中。

       误差项对于各层具有相同的定义，下面首先给出误差项的定义。假设正向传播时的计

算为：

 误差项定义为损失函数对本层输出的梯度：

所要完成的误差项传递，是根据损失函数对本层输出的梯度计算损失函数对本层输入的梯度：

       若网络中的某层（如全连接层、卷积层等）含有训练参数w，b，则可以较为方便的根据后一层传递来的损失函数对本层输出的梯度，计算损失函数对本层w、b的梯度。若该层（如激活层、池化层等）不含训练参数，则只需要完成误差项的前传即可。各层的误差项传递公式和由误差项计算损失函数对本层参数梯度的公式各不相同，下面逐一给出。

1.全连接层

       误差项前传公式：

       由误差项计算损失函数对本层参数梯度的公式：

2.卷积层

       卷积层的情况较为复杂。

       由误差项计算损失函数对本层参数梯度的公式：

误差项为一个矩阵，其shape和输出数据的shape相同。其中conv为卷积运算，误差项充当卷积核，X（l-1）充当输入图像。

       该部分在代码实现时，需要注意，在前向传播时储存X（l-1）经过img2col后的矩阵化形式（将其定义为self属性），而误差项的矩阵化表示直接通过reshape即可实现，这样便于上式的计算。

误差项前传公式：

其中rot180表示矩阵顺时针旋转180度操作。

       为便于理解，下面给出一个简单的公式示例：

该部分在代码实现时，涉及本层误差项的padding，每边补“0”的个数为kernel_size-1，同时输入图像一般情况下都为多通道，因此在进行卷积操作前，需要进行到kernel的rot180旋转以及filter的通道输入输出通道的调整。进行卷积运算时同样采用矩阵化运算。

       虽然上述误差前传公式的运算较为复杂，但仍为一般代码编写的参考依据。我受到前向传播时矩阵化运算的启发，考虑到误差前传公式能否也采用矩阵化的表达方式，并作为代码编写的依据？

3.池化层

       池化层的情况比较简单，由于我们在正向传播时，已经记录最大值在滑动窗口中的位

置，在反向传播时，对于扩充的s*s块，最大值位置处的元素设为本层误差项，其他位置全部置0：

       推导过程，假设池化函数为：

损失函数对xi的偏导数为：

在这里分两种情况，如果i=t，则有：

否则有：

4.激活层及损失函数（亮点）

       激活层包括relu和softmax两部分，他们也都不需要进行梯度计算，只需将误差前传

即可。其中relu函数误差前传较为简单，仅将本层误差项对应输入小于“0”的位置的置“0”，其他位置保持不变即可得到需要前传的误差项。

       本框架自认为的一大亮点，是在链式法则下，将损失函数对softmax输出的梯度计算和softmax对全连接层输出的梯度计算进行合并，从而直接计算出损失函数对全连接层输出的梯度，想较于常规方法减少了一次误差项前传。具体理论依据如下：

其中z为全连接层的输出向量，aj为与标签值对应的softmax输出。由前面的前向传播可以得到，等号右边第一项为-1/aj。下面考虑第二项的情况，即与标签值对应的softmax输出对全连接层输出向量的偏导数，同样是一个向量。分为如下两种情况讨论：

其中i代表全连接成输出的下标索引。将上面这两种结果分别乘以-1/aj，分别得到aj-1和aj。这非常的特殊，它的意义在于：我们在前向传播时，只需记录下softmax的输出向量，在反向传播时，即可直接获得损失函数对全连接层输出的梯度（即最后一层全连接层的误差项），获得方法为，将softmax输出向量中与标签值对应位置的值减“1”，其他位置的值保持不变。

       至此得到了各层的反向传播实现，组合起来就得到了整个卷积网络的反向传播算法计算公式。该部分的代码在实现时，需要反复debug。自认为其中的一个技巧为特别关注各个误差项的shape，该层的误差项的shape应与该层输出数据的shape相同（因为损失值为scalar，对一个矩阵的偏导，其结果应该和矩阵的shape相同）。同时需要注意，在全连接层误差项传递给前一层时，需要进行reshape。因为在前向传播进入全连接层时，也是经过reshape的。

       获得损失函数对参数的梯度后，对参数的更新较为简单，更新后的参数值=更新前的参数值-learning_rate*损失函数对该参数的梯度值。由于是对简易框架的简单测试，因此learning_rate取为常数0.01。完成一次反向传播后，需要将梯度值置零，以保证下一次反向传播的正确进行。

四 框架测试——LeNet网络

       框架在实现时考虑了喂入数据为多个样本的情况，因此可以指定batch_size的大小。同时，为了测试的简单性，仅用一个batch模拟训练集，因此优化函数相应的为批量梯度下降。随机生成一个batch_size=32的3通道28*28的输入图像，并为其生成相应数量的标签值，范围为0~9，即模拟10分类问题。

       搭建的LeNet网络包含两层卷积、池化和激活，后接两层全连接，全连接的输出经过softmax激活后通过cross_entropy函数计算损失。

       经过200个epoch的循环，发现单个样本的损失值从起初的大约2.30下降到最低时的大约1.69。且网络起初收敛速度较快，后面出现了轻微震荡，猜测这应该和超参数的设置和过于简单的优化函数有关，属于正常现象。因此可以证明网络确实从输入数据中学到了特征，可以完成简单的分类，进而证明了框架的可用性。

五 代码效率分析

       对于代码的效率分析，我主要从运算逻辑和运算性能两方面进行考虑。

       运算逻辑方面，运算的化简可以避免重复的计算，进而减小计算压力，拿我本专业的知识来举例就是FFT（快速傅里叶变换）实现了DFT（离散傅里叶变换）的加速。在本框架中，将起初的两次误差项传递化简为一次。

       运算性能方面，考虑到ndarray数据结构相比于list数据结构有数据存储方面的特殊性，进而可以实现更高效的矢量化计算，因此框架中的运算多采用ndarray的矢量化计算。另外，为了充分利用GPU的并行计算能力（虽然框架并没有实现使用GPU的相关支持），通过img2col将卷积运算转化成矩阵乘法运算。这样做也带来了一定的缺点——对输入数据的重复性存储，牺牲了内存。

六 深入思考

       在前向传播中，讨论了将输入图像经过img2col预处理后，卷积层的前向传播可以表达为Y=KX。其中X为本层输入，同时也是上一层的输出，而Y为本层的输出，那么在已知误差损失对Y的梯度的前提下，误差损失对X的梯度（也就是误差前传公式）是否可以表达为：

       根据之前技巧，乍看结果肯定是有问题，因为shape和输入数据的shape不同。但进一步思考，这是输入数据经过img2col后的shape，那我是不是只要对其进行col2img（不知道是否已经存在这种处理）处理后就可以将此误差传递给前一层？关于如何进行col2img我做了如下思考（仅考虑单样本的情况）：

       假设输入数据的shape为（3，64， 64），那么通过上式计算得到要前传的误差项shape应为（27，62*62），这里的每一列代表一个filter大小的输入数据，27*62*62>>3*64*64是因为经过img2col后牺牲了内存，存在数据重复存储。那只要从62*62列中进行抽取即可还原出输入数据，抽取的间隔应该是kernel_size-1，最后不能整除的部分，经过计算也是可以实现的。

随后经过搜索资料发现col2img早已有人实现。因为时间原因，自己也没来的及验证上述误差项前传的正确性，但我感觉这种方法也已经被实现。最后，无论如何，这都是一次不错的深入思考。

最后，该汇报结合自己之前的所学和这几天的努力所得到的理解写出，如有错误，希望各位指出。

参考文献：

卷积层反向

反向传播之六：CNN 卷积层反向传播 - 知乎

全连接层

神经网络全连接层反向传播公式推导过程 - 知乎

Numpy实现神经网络全连接层_AkagiSenpai的博客-CSDN博客_损失函数对输入矩阵的偏导

池化

池化层（pooling）的反向传播是怎么实现的_贾世林jiashilin的博客-CSDN博客

https://www.phpyuan.com/260727.html

2020.6.28