【入门向】光流法(optical flow)基本原理+深度学习中的应用【FlowNet】【RAFT】
目录
- 1. 理论背景
-
- 1.1 光流
- 1.2 光流场
- 2. 基本原理
-
- 2.1 假设条件
- 2.2 约束方程
- 3. 光流估计方法
-
- 3.1 思路概述
- 3.2 优缺点对比
- 4. 稠密光流和稀疏光流
-
- 4.1 稠密光流
- 4.2 稀疏光流
- 4.3 优缺点对比
- 5. 光流法在深度学习中的应用
-
- 5.1 FlowNet
-
- 5.1.1 FlowNetS编码器
- 5.1.2 FlowNetCorr编码器
- 5.1.3 FlowNetS和FlowNetCorr解码器
- 5.2 RAFT
-
- 5.2.1 特征提取
- 5.2.2 视觉相似性计算
- 5.2.3 迭代更新
- 5.3 RAFT和RAFT-S的区别
1. 理论背景
1.1 光流
光流(optical flow)是空间运动物体在成像平面上的像素运动的瞬时速度。
通常将一个描述点的瞬时速度的二维矢量 u ⃗ = ( u , v ) \vec u = (u,v) u=(u,v)称为光流矢量。
1.2 光流场
空间中的运动场转移到图像上就表示为光流场(optical flow field)。
- 光流场是很多光流的集合;
- 构建光流场是试图重建运动场,进行运动分析,理想情况下,光流场对应于运动场。
2. 基本原理
2.1 假设条件
1. 像素亮度恒定不变
同一像素点在不同帧中的亮度是不变的,这是光流法使用的基本假定(所有光流法及其变种都必须满足),从而可以得到2.2中的约束方程。
2. 时间连续/运动很微小
时间的变化不会引起目标位置的剧烈变化,即相邻帧之间的位移很小。
2.2 约束方程
I ( x , y , t ) = I ( x + d x , y + d y , t + d t ) ( 1 ) I(x,y,t)=I(x+\mathrm d x, y+\mathrm d y, t+\mathrm d t) \qquad(1) I(x,y,t)=I(x+dx,y+dy,t+dt)(1)对右式进行泰勒展开 = I ( x , y , t ) + ∂ I ∂ x d x + ∂ I ∂ y d y + ∂ I ∂ t d t + ϵ =I(x,y,t)+\frac {\partial I}{\partial x}\mathrm d x+\frac {\partial I}{\partial y}\mathrm d y+\frac {\partial I}{\partial t}\mathrm d t+\epsilon =I(x,y,t)+∂x∂Idx+∂y∂Idy+∂t∂Idt+ϵ其中, ϵ \epsilon ϵ是二阶无穷小,可以忽略不计。将 ( 1 ) (1) (1)式左右两侧同除 d t \mathrm dt dt可以得到下式: ∂ I ∂ x d x d t + ∂ I ∂ y d y d t + ∂ I ∂ t d t d t = 0 ( 2 ) \frac {\partial I}{\partial x} \frac {\mathrm dx}{\mathrm dt}+\frac {\partial I}{\partial y} \frac {\mathrm dy}{\mathrm dt}+\frac {\partial I}{\partial t} \frac {\mathrm dt}{\mathrm dt}=0 \qquad(2) ∂x∂Idtdx+∂y∂Idtdy+∂t∂Idtdt=0(2)此处我们做以下人为规定: { ∂ I ∂ x = I x ∂ I ∂ x = I y ∂ I ∂ x = I t ( 3 ) d x d t = u d y d t = v \begin{cases} \frac {\partial I}{\partial x}=I_x\\ \frac {\partial I}{\partial x}=I_y\\ \frac {\partial I}{\partial x}=I_t \qquad(3)\\ \frac {\mathrm dx}{\mathrm dt}=u\\ \frac {\mathrm dy}{\mathrm dt}=v \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧∂x∂I=Ix∂x∂I=Iy∂x∂I=It(3)dtdx=udtdy=v将 ( 3 ) (3) (3)带入 ( 2 ) (2) (2)中,得到: I x u + I y v + I t = 0 ( 4 ) I_x u+I_y v +I_t=0 \qquad(4) Ixu+Iyv+It=0(4)其中 I x I_x Ix, I y I_y Iy均可以由图像求得, ( u , v ) (u,v) (u,v)即为光流矢量。
约束方程有一个,但未知量有两个,因此需要引入额外的约束条件,从不同角度引入约束也就产生了不同的光流计算方法。
3. 光流估计方法
3.1 思路概述
① 基于梯度的方法(微分法)
利用时变图像灰度的时空微分(时空梯度函数)来计算像素的速度矢量。
② 基于匹配的方法
有基于特征和基于区域两种。
- 基于特征的方法是对目标特征进行定位和跟踪,目标大的运动和亮度具有更好的鲁棒性。
- 基于区域的方法是对类似的区域进行定位,通过相似区域的位移计算光流。
③ 基于能量的方法(频率)
要获得均匀光流场的准确的速度估计,必须对输入图像进行时空滤波处理,即对时间和空间进行整合。
④ 基于相位的方法
由Fleet和Jepon最先提出,将相位信息用于光流的计算。
⑤ 神经动力学方法
利用神经网络建立的视觉运动感知的神经动力学模型是对生物视觉系统功能与结构较为直接的模拟。
3.2 优缺点对比
| 方法 | 优点 | 缺点 |
|---|---|---|
| 基于梯度 | 计算简单,结果较好 | 对于变化需“平滑”的要求较高 |
| 基于匹配(特征) | 对目标大的运动和亮度变化具有鲁棒性 | 特征的提取和精准匹配困难,估计亚像素精度的光流困难,计算量大 |
| 基于匹配(区域) | 适用于视频编码 | 光流不稠密,估计亚像素精度的光流困难,计算量大 |
| 基于能量 | 运算思路简单 | 光流的时间和空间分辨率被降低,需要可靠结果的计算量大 |
| 基于相位 | 相位信息更加可靠,获得的光流场具有更好的鲁棒性 | 时间复杂性高,精度的提高需要消耗大量时间,对图像序列的时间混叠敏感 |
| 神经动力学 | 对生物视觉系统的直接模拟 | 方法仍不成熟 |
4. 稠密光流和稀疏光流
4.1 稠密光流
逐点匹配,计算图像上所有点的偏移量,形成一个稠密的光流场。
4.2 稀疏光流
对指定的一组点(最好是具有某种明显的特征,也就是利用上文“基于特征的方法”)进行跟踪。
4.3 优缺点对比
| 光流类型 | 优点 | 缺点 |
|---|---|---|
| 稠密光流 | 配准的精准度高,效果好 | 由于要计算每个像素点的偏移量,计算量大,时效性差 |
| 稀疏光流 | 计算量小 | 需要被跟踪的点具有较为明显的特征 |
5. 光流法在深度学习中的应用
5.1 FlowNet
《FlowNet: Learning Optical Flow with Convolutional Networks》
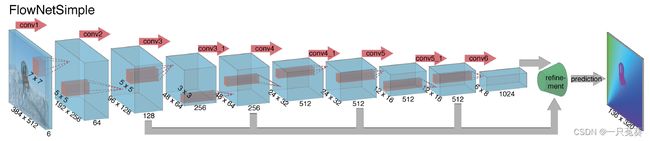
此架构由FlowNetS(Simple) 和FlowNetCorr两种,结构均类似U-Net:

5.1.1 FlowNetS编码器
输入为两相邻帧图像,通道数为6,前3是前一帧图,后3是后一帧图。该架构允许网络自行决定如何处理两个相堆叠的图像。
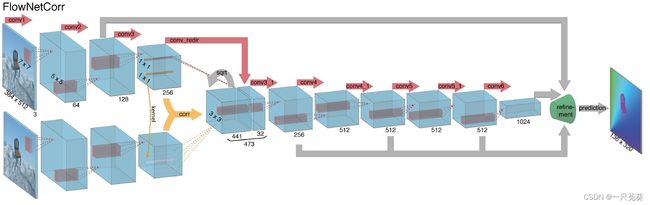
5.1.2 FlowNetCorr编码器
只接受一帧作为输入,第一阶段CNN的权值共享,从两帧图像中计算出两个特征映射 f 1 \mathbf f_1 f1和 f 2 \mathbf f_2 f2。
FlowNetCorr与前者最大的区别就是引入了一种叫“相关层”的新技术,相关性的计算是乘法补丁比较(multiplicative patch comparisons),给定两个多通道特征图 f 1 , f 2 : R 2 → R c \mathbf f_1, \mathbf f_2 : \Bbb R^2 \to \Bbb R^c f1,f2:R2→Rc,其中 w , h , c w,h,c w,h,c分别表示宽度、高度和通道数,将两个特征映射进行乘法块比较,计算公式为: c ( x 1 , x 2 ) = ∑ o ∈ [ − k , k ] × [ − k , k ] ⟨ f 1 ( x 1 + o ) , f 2 ( x 2 + o ) ⟩ ( 5 ) c(\mathbf x_1, \mathbf x_2) = \sum _{\mathbf o \in [-k,k] \times [-k,k]} \langle \mathbf f_1(\mathbf x_1 +\mathbf o), \mathbf f_2(\mathbf x_2+\mathbf o)\rangle \qquad(5) c(x1,x2)=o∈[−k,k]×[−k,k]∑⟨f1(x1+o),f2(x2+o)⟩(5)方块图尺寸为 K : = 2 K + 1 K:=2K+1 K:=2K+1,公式 ( 5 ) (5) (5)的计算实际上就是卷积运算,只不过这里的卷积核是不可训练的,而是用已设定好的权重参数进行卷积运算。
值得一提的是,两幅特征图并没有做全局关联,而是在局部上进行运算。在特征图匹配完成后,相关结果前向传播到后续卷积层,进一步提取更顶层的特征。
5.1.3 FlowNetS和FlowNetCorr解码器
为了既保留从较粗的特征图中传递的高层信息,又保留较低层的精细局部信息,作者设计了下图:
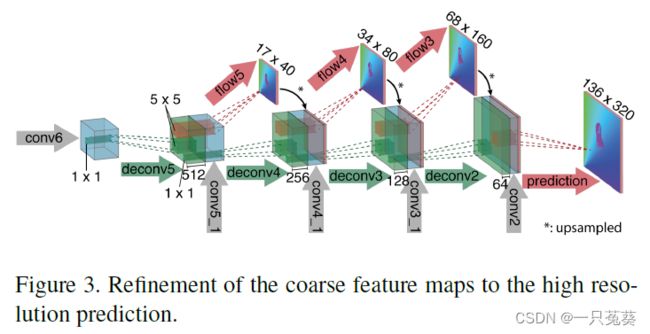
编码器输出特征图的分辨率缩小为原始图像的 1 64 \frac 1{64} 641,在解码器中使用可训练的上采样卷积层,每个解码阶段将上一阶段的放大结果和编码器相应层的特征图连接起来,这样有助于网络预测细节。
使用的上采样方法为计算成本较低的双线性上采样。
5.2 RAFT
《RAFT: Recurrent All-Pairs Field Transforms for Optical Flow》 RAFT代码
与FlowNet类似,RAFT架构同样有两种:RAFT和RAFT-S,后者是其轻量级版本。
RAFT由三个主要部分构成:
- 一个特征提取器,为每个像素提取出一个特征向量;
- 一个相关层,为所有像素对产生一个四维“相关体积”,随后汇集产生一个较低分辨率的“体积”;
- 一个基于GRU的循环更新运算器,从“相关体积”中检索数值并迭代更新光流场。
接下来,对这三个部分进行详细介绍。
5.2.1 特征提取
编码特征提取 g θ g_{\theta} gθ输入类似于FlowNetCorr,也是分别输入两个连续帧图像,从图像中分别提取特征。卷积构架由6个残差层组成(同ResNet)。

另外,作者还引入了一个上下文网络,上下文网络仅仅从第一张输入图像中提取特征,网络结构 h θ h_{\theta} hθ和前面的 g θ g_{\theta} gθ是一样的。
特征提取模块由编码特征提取 g θ g_{\theta} gθ和上下文网络 h θ h_{\theta} hθ两部分共同阻证,两者均只执行一次。
5.2.2 视觉相似性计算
视觉相似性计算的是所有特征图对的内积,从而得到一个名为“相关体积”的四维张量,其中包含了关于大小像素位移的关键信息。

与FlowNetCorr的相关层不同,此处计算的是两个特征图的全局相关性,没有任何固定大小的窗口,可以用下式表示: C i j k l = ∑ d f 1 i j d ⋅ f 2 k l d ( 6 ) \mathrm C_{ijkl} = \sum_d \mathbf {f_1}_{ijd} \cdot \mathbf {f_2}_{kld} \qquad(6) Cijkl=d∑f1ijd⋅f2kld(6)将四维张量的后两维使用大小分别为 1 , 2 , 4 , 8 1,2,4,8 1,2,4,8的核进行池化,形成相关金字塔。利用相关金字塔建立多尺度图像相似性特征,使突变运动更为明显,也同时提供了关于大位移和小位移的信息。
5.2.3 迭代更新
使用一个门控循环单元(GRU)序列,来结合之前获取的所有数据。

更新算子从初始值 f 0 = 0 \mathbf f_0 = 0 f0=0开始估计一连串的光流值 { f 1 , . . . , f N } \{\mathbf f_1, ..., \mathbf f_N\} {f1,...,fN}。每次迭代产生一个更新方向 Δ f \Delta \mathbf f Δf,并应用于当前估计值: f k + 1 = Δ f + f k + 1 \mathbf f_{k+1}=\Delta \mathbf f+\mathbf f_{k+1} fk+1=Δf+fk+1。
5.3 RAFT和RAFT-S的区别
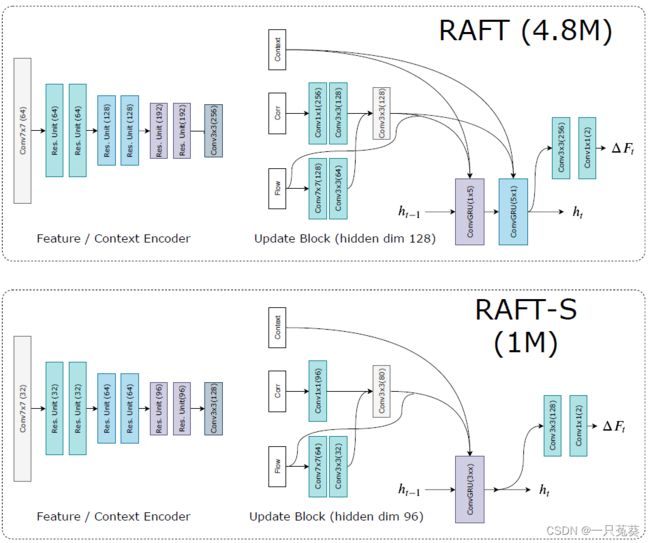
在RAFT-S中用瓶颈残差单元(bottleneck residual units) 取代残差单元;RAFT使用两个GRU更新块,大小分别为 1 × 5 1 \times 5 1×5和 5 × 1 5 \times 1 5×1,RAFT-S只使用一个GRU更新块,大小为 3 × 3 3 \times 3 3×3。
图中可以看到两者的运算量还是有比较大的区别。
参考博客:
计算机视觉–光流法(optical flow)简介
OpenCV进阶(2)OpenCV中的光流
RAFT:使用深度学习的光流估计