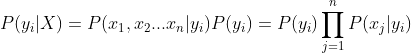朴素贝叶斯分类器原理解析与python实现

       贝叶斯分类器是以贝叶斯原理为基础的分类器的总称，是一种生成式模型，朴素贝叶斯分类器是其中最简单的一种。要高明白贝叶斯分类器的原理，首先得明白一些基本概念。

预备知识

• 基本概念

       先验概率：根据统计/经验得到的某事情发生的概率，比如北京下雨的概率可以通过以往的经验或者统计结果得到

       后验概率：在一定条件下某事情发生的概率，比如北京天空出现乌云(因)会下雨(果)的概率

       条件概率：事情发生时某条件出现的概率，比如北京下雨(果)会出现乌云(因)的概率

• 贝叶斯公式

                                                 

       设A表示事件，B表示A发生的影响因素，那么有：

       为先验概率，即事件A的发生不用考虑影响因素B

       为后验概率，表示在因素B的条件下A发生的概率

       为条件概率，表示事件A发生的条件下因素B发生的概率

       为归一化因子，这里B是已知的，相当于一个常量，不影响其他概率

       总结：后验概率=先验概率*条件概率

朴素贝叶斯分类器

       朴素贝叶斯分类器就是利用贝叶斯原理实现的，在分类问题中，类别C相当于事件A，特征X相当于影响因素B，那么贝叶斯公式可以改写为如下形式，它表示的含义是当特征为X时，X属于类别C的概率

                                  

• 贝叶斯分类器

       设类别C={}，特征向量X={}，贝叶斯分类器的工作原理如下：

       1)求解在X条件下每个类别的概率即求得

       2)中概率最大的项对应的类别即为X的预测类别

       贝叶斯分类器的工作原理：寻找中的最大值，最大值对应的类别即为预测类别。然而在实际情况中往往无法直接求得，所以根据贝叶斯公式将求解转化为求解。P(X)与类别无关且为固定值，不会影响中的最大值的求解，因此将式子简化为如下形式

                                                                   

       总结：贝叶斯分类器就是最大后验概率估计

• 朴素贝叶斯分类器

      何为朴素？朴素代表着特征向量X={}中每一个特征相互独立。那么朴素贝叶斯分类器可以表达为：

                                      

      当每一个特征相互独立时，上面的式子可以变形为如下形式：

                                      

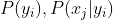• 的求解

       是无法直接计算的，只能通过样本来估计，因此样本量不能太少。 先验概率表示类别为的样本数量在整个样本集中所占比例(当做概率的估计)

       当为离散型时：

       表示在类别为的样本中，第j个特征出现次数占总的类别为的样本的比例(当做概率的估计)。这里你可能会问，每个类别为的样本中必然会存在第j个特征啊？由于特征有多个取值，所以实际表示的是特征取值为时的概率，在统计时需要将特征每一个取值时的概率都计算出来，当预测一个新样本时，如果特征取值为，则特征取值为的概率参与计算，其他取值的概率则不参与计算。

       当为连续型时：

       假设服从某一个概率分布模型，由样本去求解模型参数(可以通过极大似然估计求解)

• Laplace校准

       在统计样本时，如果出现，会导致为0，这显然是不合理的，为了避免这种情况的发生，采用Laplace校准：将第j个特征出现次数+1以避免出现；同理，所以也采用Laplace校准。

朴素贝叶斯分类器Python实现

def NaiveBayes(traindata, trainlabel):
    '''
    通过训练集计算先验概率分布p(c)和条件概率分布p(x|c)
    :param traindata: 训练数据集   (m,n)
    :param trainLabel: 训练标记集  (m,1)
    :return: p(c)和p(x|c)
    '''

    classes = 10  # 类别数
    features = 784  # 样本的维度

    sampleNum = trainlabel.shape[0]

    # 计算p(c)
    Pc = np.zeros((classes, 1))
    for c in range(classes):
        c_i = (trainlabel == c)  # 统计标签中类别为c的样本数量
        c_i_num = np.sum(c_i)
        Pc[c] = (c_i_num+1)/sampleNum  # Laplace校准
    Pc = np.log(Pc)

    # 计算p(x|c)
    y_num = 2  # 每个特征可能的取值的个数
    c_f_y_count = np.zeros((classes, features, y_num))  # 统计每个类别每个特征的每种可能取值出现的次数
    for k in range(sampleNum):
        c = trainlabel[k]
        data = traindata[k]
        for f in range(features):
            y = data[f]
            c_f_y_count[c][f][y] += 1

    Px_c = np.zeros((classes, features, y_num))   # 统计每个类别每个特征的每种可能取值的概率
    for c in range(classes):
        for f in range(features):
            c_f_y_num = np.sum(c_f_y_count[c][f])
            for y in range(y_num):
                Px_c[c][f][y] = np.log((c_f_y_count[c][f][y]+1)/c_f_y_num)  # Laplace校准

    return Pc, Px_c


def predict(Pc, Px_c, x):
    '''
    根据先验概率分布p(c)和条件概率分布p(x|c)对新样本进行预测
    '''
    classes = 10
    features = 784

    Pc_x = [0]*classes  # 记录每个类别的后验概率
    for c in range(classes):
        Px_c_sum = 0
        for f in range(features):
            Px_c_sum += Px_c[c][f][x[f]]  # 对概率值取log 连乘变成了求和运算

        Pc_x[c] = Px_c_sum + Pc[c]

    pre_c = Pc_x.index(max(Pc_x))  # 找到每个类别的后验概率中的最大值对应的类别

    return pre_c


def test(Pc, Px_c, testdata, testlabel):
    sampleNum = testlabel.shape[0]

    count = 0.0
    for i in range(sampleNum):
        data = testdata[i]
        label = testlabel[i]
        pre_label = predict(Pc, Px_c, data)
        if(pre_label == label):
            count += 1

    acc = count / sampleNum

    return acc


if __name__ == '__main__':
    #加载训练集和验证集
    traindata, trainlabel = loadData('../Mnist/mnist_train.csv')
    evaldata, evallabel = loadData('../Mnist/mnist_test.csv')

    Pc, Px_c = NaiveBayes(traindata, trainlabel)

    accuracy = test(Pc, Px_c, evaldata, evallabel)
    print('accuracy rate is:', accuracy)