决策树(二) CART、决策树中的超参、决策树局限性
文章目录
- 一、CART
- 1、简单介绍
-
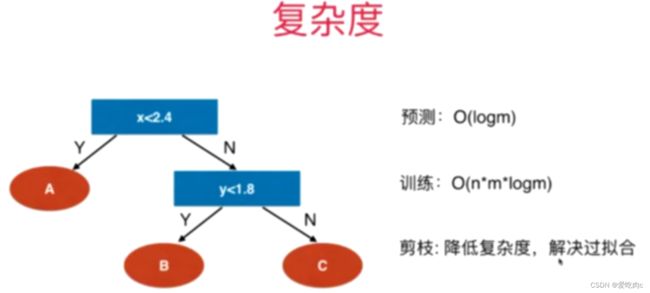
- 2、复杂度
- 3、决策树中的一些超参数
- 二、决策树解决回归问题
- 三、决策树的局限性
-
- 1、决策边界总是平行于x轴
- 2、对个别的数据敏感
一、CART
1、简单介绍
我们之前探讨的不论是信息熵还是基尼系数均属于CART
sklearn实现决策树的方式是CART,当然也可以使用其他方式
如ID3,C4.5
2、复杂度
利用一些超参数来进行降低复杂度的操作
3、决策树中的一些超参数
import numpy as np
from sklearn import datasets
x,y=datasets.make_moons(noise=0.25,random_state=666)
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.show()
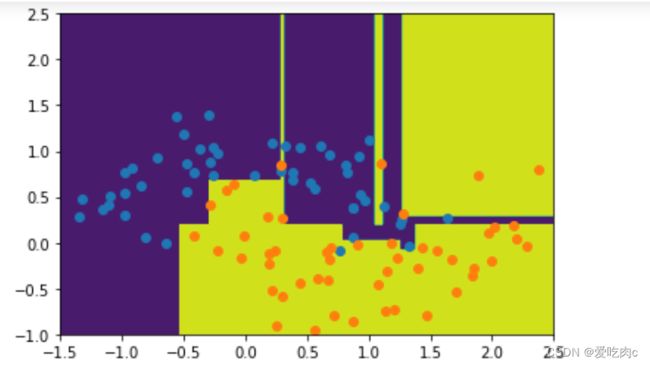
不传任何参数时 过拟合
from sklearn.tree import DecisionTreeClassifier
de_clf=DecisionTreeClassifier()#不传参数
de_clf.fit(x,y)
def plot_decision_boundary(model,axis):
x0,x1=np.meshgrid(
np.linspace(axis[0],axis[1],int((axis[1]-axis[0]))*100).reshape(-1,1),
np.linspace(axis[2],axis[3],int((axis[3]-axis[2]))*100).reshape(-1,1)
)
x_new=np.c_[x0.ravel(),x1.ravel()]
y_predict=model.predict(x_new)
zz=y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_camp=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0,x1,zz,linewidth=5,camp=custom_camp)
plot_decision_boundary(de_clf,[-1.5,2.5,-1.0,2.5])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1]) #过拟合
plt.show()
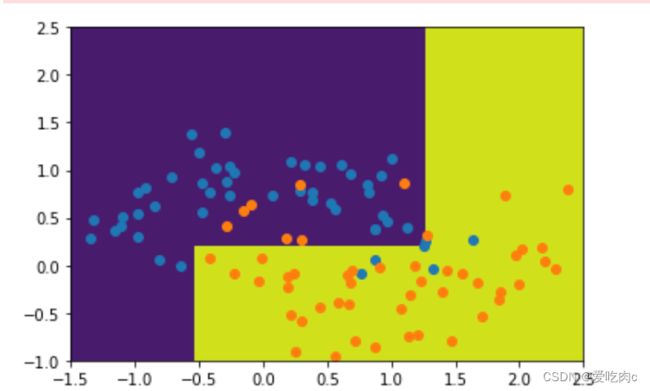
de_clf2=DecisionTreeClassifier(max_depth=2)
de_clf2.fit(x,y)
plot_decision_boundary(de_clf2,[-1.5,2.5,-1.0,2.5])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1]) #过拟合
plt.show()
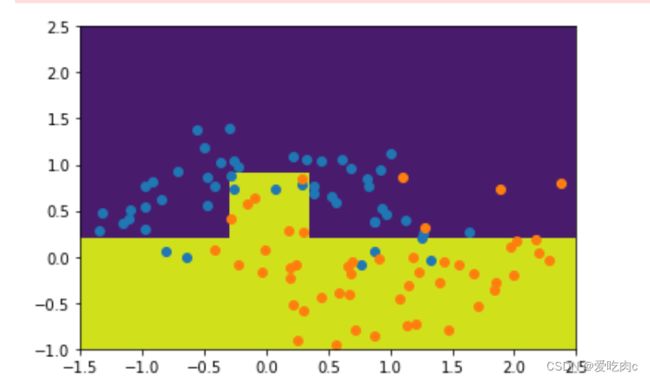
de_clf2=DecisionTreeClassifier(min_samples_leaf=6)
de_clf2.fit(x,y)
plot_decision_boundary(de_clf2,[-1.5,2.5,-1.0,2.5])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1]) #过拟合
plt.show()
de_clf2=DecisionTreeClassifier(min_samples_split=10)
de_clf2.fit(x,y)
plot_decision_boundary(de_clf2,[-1.5,2.5,-1.0,2.5])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1]) #过拟合
plt.show()
二、决策树解决回归问题
from sklearn.tree import DecisionTreeRegressor
dt_gr=DecisionTreeRegressor()
不在具体叙述
解决回归问题与解决分类问题的超参数是一致的
同理感兴趣的同学可以使用学习曲线 通过调节参数
来看是否有过拟合和欠拟合的问题

三、决策树的局限性
1、决策边界总是平行于x轴
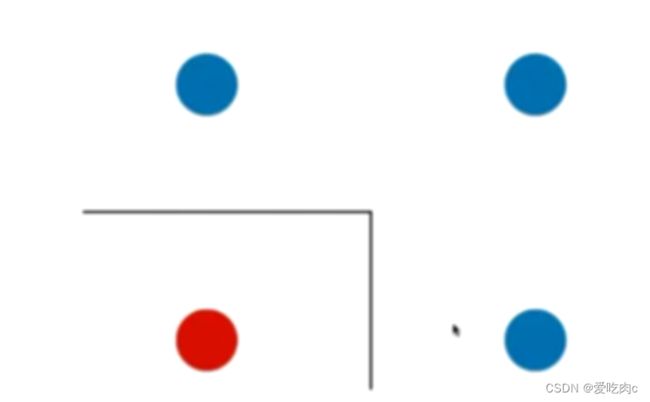
如图,该图得到的决策边界可能是这个样子,但是真实的决策边界应为:
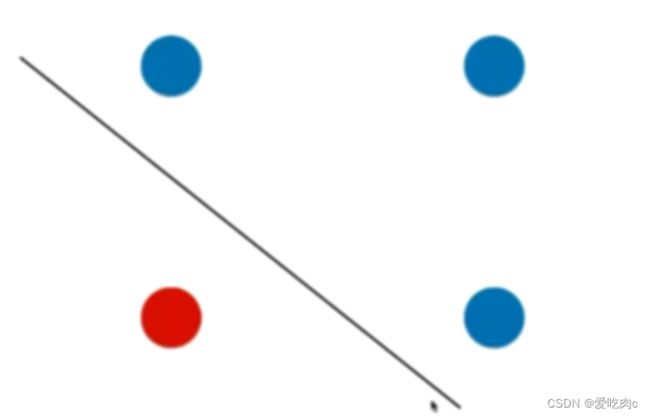
使用决策树无法得到倾斜的线,总是垂直于x或y轴的