【步态识别】MT3D 算法学习《Gait Recognition with Multiple-Temporal-Scale 3D Convolutional Neural Network》

1. 论文&代码源

《Gait Recognition with Multiple-Temporal-Scale 3D Convolutional Neural Network》
论文地址：https://dl.acm.org/doi/10.1145/3394171.3413861
代码下载地址： 作者未提供

2. 论文亮点

1. 采用3D CNN提取时空特征，使用多时间尺度框架整合不同尺度的时间信息

以BasicBlock3D模块作为基本的3D CNN块，使用局部变换模块实现3D CNN模块的大尺度区间分支；

2. 引入帧池化算法进行标准化

帧池化操作使输入序列具有相同的长度，从而使模型能够你和不同长度的视频序列，利用GAP和GMP生成多个水平特征分量，提高特征表示能力；

3. 实现最佳性能
在CASIA-B和OU-ISIR上优于大多数先进方法，在you携带物等复杂条件下的性能优势显著。

3. 模型结构

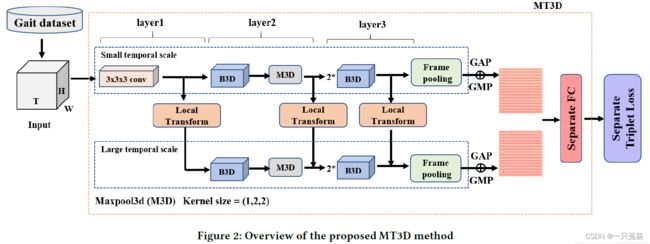
下图展示了本步态识别方法的概况图。
首先提取视频中的每一帧的剪影，将这个剪影序列送入MT3D模型，模型将会输出每个样本对应的步态特征。
MT3D模型是本文步态识别方法的核心，它包括一个双分支结构和几个关键组件：BasicBlock3D、局部变换模块、帧池化等。

3.1 MT3D

为了更好地利用步态序列的时空信息，作者提出了一个新的3D CNN模型MT3D。通过在序列层面构建两个分支，及小时间尺度和大时间尺度，双分支结构具有以下两个优点：

1.能够充分利用不同时间尺度的时间信息
帧池化能够消除固定大小输入的限制；小时间尺度可以利用整个序列的帧的关系学习更具判别性的时空特征；大时间尺度可以在序列间提取更具鲁棒性的局部时空特征。

2.这两个分支都可以通过经典的操作轻松实现
两个分支均可以通过简单的卷积、池化等操作实现，并且分支的结构是想死，因此，小时间尺度分支点信息可以多次整合到大时间尺度的分支中，提高特征的表示能力。

3.2 局部变换模块（Local Transform）

小时间尺度分支倾向于关注连续帧之间的强关系，而忽略局部时间间隔之间的关系，为了利用被忽略的这部分信息，来聚合每个局部时间间隔中的信息，作者设计了局部变换模块。
首先给定一个序列$\tilde{X}=\{X_1,X_2,...,X_N\}$，其中$N$是整个步态剪影序列的长度，局部序列可以由下式切割而成：$$C_i=F(X_{(i-1)\times s+1},X_{(i-1)\times s+2},...,X_{(i-1)\times s+s}),i=1,2,...,[\frac{N}{2}]$$

$C_i$表示的是第$i$个剪辑片段；$s$是剪辑索引时的移动步长，也是局部时间间隔的长度；$F(\cdot )$表示的是聚合操作，它主要有两种使用表达式：
$$①最大值/平均值F(\cdot )=\alpha {\text{Max}}^{s\times 1\times 1}(\cdot )+\beta {\text{Mean}}^{s\times 1\times 1}(\cdot )$$其中，$\alpha$, $\beta$赋值$0$或$1$

$$②卷积F(\cdot )=c^{s\times 1\times 1}(\cdot )$$其中$(s,1,1)$是卷积核大小也是步长。

3.3 BasicBlock3D（B3D）

受低秩结构的启发，作者提出了一种新的3D CNN模块，名为BasicBlock3D，旨在通过结合传统的3D CNN和低秩结构来学习更具判别性和稳定性的时空特征。

此模块具有两个分支，一是以传统的3D卷积为主干提取时空特征。二是使用低秩结构作为分支，进一步提高主干的表示能力。

对于传统的3D CNN：
$$X_{i+1}=c^{3\times 3\times 3}(X_i)$$其中，$X_i\in {\mathbb{R}}^{C_i\times T\times H\times W}$和$X_{i+1}\in {\mathbb{R}}^{C_{i+1}\times T\times H\times W}$分别是第$i$层和第$i+1$层的输出；$C_i$和$C_{i+1}$是通道数；$T$是步态序列长度；$(H,W)$是图像大小。

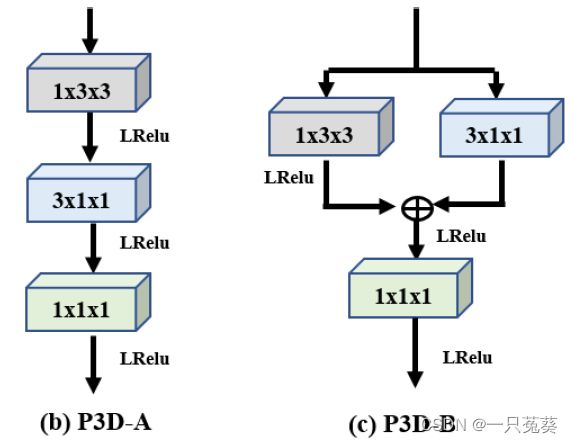
由于传统3D CNN具有参数冗余、表示能力弱的缺点，为了更有效地利用时空信息，作者引入了低秩结构来实现BasicBlock3D的另一个分支$$low-rank\{\begin{array}{l}P3D-A:X_{i+1}=c^{1\times 1\times 1}(c^{3\times 1\times 1}(c^{1\times 3\times 3}(X_i)))\\ P3D-B:X_{i+1}=c^{1\times 1\times 1}(c^{1\times 3\times 3}(X_i)+c^{3\times 1\times 1}(X_i))\end{array}$$

将两个分支结合起来，（并进行了一些细节调整）得到B3D的两种结构：$$B3D\{\begin{array}{l}B3D-A:X_{i+1}=c^{3\times 3\times 3}(X_i)+c^{1\times 1\times 1}(c^{3\times 1\times 1}(c^{1\times 3\times 3}(X_i)))\\ B3D-B:X_{i+1}=c^{3\times 3\times 3}(X_i)+c^{1\times 3\times 3}(X_i)+c^{3\times 1\times 1}(X_i)\end{array}$$

3.4 帧池化和特征映射（Frame Pooling and Feature Mapping）

3.4.1 帧池化（Frame Pooling）

输入$X_{in}\in {\mathbb{R}}^{C_{in}\times T_{in}\times H_{in}\times W_{in}}$$$X_{out}=\alpha {\text{Max}}^{T_{in}\times 1\times 1}(X_{in})+\beta {\text{Mean}}^{T_{in}\times 1\times 1}(X_{in})$$其中，$\alpha$, $\beta$为$0$或$1$；输出大小固定的特征图$X_{out}\in {\mathbb{R}}^{C_{in}\times 1\times H_{in}\times W_{in}}$
为了使特征更具判别性，将$X_{out}$进行水平分割，得到多个特征条，对每个特征条应用GAP和GMP生成相应的水平分量。

3.4.2 特征映射

$$Y={\text{Separate}}_{fc}({\text{Max}}^{1\times 1\times W_{in}}(X_{out})+{\text{Avg}}^{1\times 1\times W_{in}}(X_{out}))$$其中，${\text{Separate}}_{fc}$是独立的全连接层，可以进一步整合通道信息；输出$Y\in {\mathbb{R}}^{C_{out}\times 1\times H_{in}\times 1}$

4. 实验结果

4.1 CASIA-B

4.2 OU-ISIR

4.3 消融实验

5. 总结

本文提出了一种基于多时间尺度3D CNN的新型步态识别方法。通过梳理大小时间尺度的时空特性，MT3D可以更好地提取步态序列剪影的信息。在基准数据集上的实验表明，所提出的方法已经取得了最先进的性能，且MT3D框架对复杂条件更加稳健。

在未来，我们将探索如何在样本少的条件下提高步态识别的性能。

参考博客：

多时间尺度 3D 卷积神经网络的步态识别