【pytorch优化器】Adagrad、RMSProp优化算法详解

转载自：
https

一、简介

模型每次反向传导 都会给各个可学习参数p 计算出一个偏导数g_t，用于更新对应的参数p。通常偏导数g_t 不会直接作用到对应的可学习参数p上，而是通过优化器做一下处理，得到一个新的值 ，处理过程用函数F表示（不同的优化器对应的F的内容不同），即，然后和学习率lr一起用于更新可学习参数p，即。

二、Adagrad原理

我们经常使用梯度下降算法来完成神经网络的训练以及优化，梯度下降算法它的收敛速度会很慢，为了解决它的问题，出现了一些在梯度下降算法基础之上的新算法，有一种算法叫做Adagrad算法，它相比于梯度学习算法能够加快深层神经网络的训练速度。因此，它非常适合处理稀疏数据。AdaGrad可大大提高SGD的鲁棒性。

AdaGrad：全称Adaptive Gradient，自适应梯度，是梯度下降优化算法的扩展。Adagrad优化算法被称为自适应学习率优化算法，随机梯度下降SGD对所有的参数都使用的固定的学习率进行参数更新，但是不同的参数梯度可能不一样，所以需要不同的学习率才能比较好的进行训练，但是这个事情又不能很好地被人为操作，所以 Adagrad 便能够帮助我们做这件事。

Adagrad优化算法就是在每次使用一个 batch size 的数据进行参数更新的时候，算法计算所有参数的梯度，那么其想法就是
对于每个参数，初始化一个变量 s 为 0，然后每次将该参数的梯度平方求和累加到这个变量 s 上，然后在更新这个参数的时候，学习率就变为

所以 更新参数值公式为： x = x - g_x * new_lr(上面的公式), 其中g_x是梯度值。

这里的 ϵ是为了数值稳定性而加上的，因为有可能 s 的值为 0，那么 0 出现在分母就会出现无穷大的情况，通常 ϵ 取 10的负10次方，这样不同的参数由于梯度不同，他们对应的 s 大小也就不同，所以上面的公式得到的学习率也就不同，这也就实现了自适应的学习率。
我们使用自适应的学习率就可以帮助算法在梯度大的参数方向减缓学习速率，而在梯度小的参数方向加快学习速率，这就导致了神经网络的训练速度的加快。

Adagrad算法代码实现

def sgd_adagrad(parameters, sqrs, lr):
	eps = 1e-10
	for param, sqr in zip(parameters, sqrs):
	sqr[:] = sqr + param.grad.data ** 2
	div = lr / torch.sqrt(sqr + eps) * param.grad.data
	param.data = param.data - div

Adagrad的核心想法就是，如果一个参数的梯度一直都非常大，那么其对应的学习率就变小一点，防止震荡，而一个参数的梯度一直都非常小，那么这个参数的学习率就变大一点，使得其能够更快地更新，这就是Adagrad算法加快深层神经网络的训练速度的核心。

三、RMSProp原理

RMSProp全称为Root Mean Square Propagation，是一种未发表的自适应学习率方法，由Geoff Hinton提出，是梯度下降优化算法的扩展。

AdaGrad的一个限制是，它可能会在搜索结束时导致每个参数的步长(学习率)非常小，这可能会大大减慢搜索进度，并且可能意味着无法找到最优值。RMSProp和Adadelta都是在同一时间独立开发的，可认为是AdaGrad的扩展，都是为了解决AdaGrad急剧下降的学习率问题。

• RMSProp采用了指数加权移动平均(exponentially weighted moving average)。
• RMSProp比AdaGrad只多了一个超参数，其作用类似于动量(momentum)，其值通常置为0.9。
• RMSProp旨在加速优化过程，例如减少达到最优值所需的迭代次数，或提高优化算法的能力，获得更好的最终结果。

举例说明

假设损失函数是，即我们的目标是学习x和y的值，让Loss尽可能小。

如下是绘制损失函数的代码以及绘制出的结果。注意这并不是一个U型槽，它有最小值点，这个点对应的x和y值就是学习的目标。

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
 
def func(x, y):
    return x * x + 10 * y * y
 
def paint_loss_func():
    x = np.linspace(-50, 50, 100) #x的绘制范围是-50到50，从改区间均匀取100个数
    y = np.linspace(-50, 50, 100) #y的绘制范围是-50到50，从改区间均匀取100个数
    
    X, Y = np.meshgrid(x, y)
    Z = func(X, Y)
 
    fig = plt.figure()#figsize=(10, 10))
    ax = Axes3D(fig)
    plt.xlabel('x')
    plt.ylabel('y')
 
    ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
    plt.show()
 
paint_loss_func()

通过解析求解，显然当时，Loss取得最小值。但这里我们通过神经网络反向传播求导的的方式，一步步优化参数，让Loss变小。通过这个过程，可以看出RMSProp算法的作用。

假设x和y的初值分别为，此时对Loss函数进行求导，x和y的梯度分别是，显然x将要移动的距离小于y将要移动的距离，但是实际上x离最优值0更远，差距是40，y离最优值0近一些，距离是20。因此SGD给出的结果并不理想。

RMSProp算法有效解决了这个问题。通过累计各个变量的梯度的平方r，然后用每个变量的梯度除以r，即可有效缓解变量间的梯度差异。如下伪代码是计算过程:

下图是训练10次，x和y的移动轨迹，其中红色对应SGD，蓝色对应RMSProp。
观察SGD对应的红色轨迹，由于y的梯度很大，y方向移动过多，一下从坡一边跑到了另一边，而x的移动却十分缓慢。但是通过RMSProp，有效消除了梯度差异导致的抖动。

训练过程的代码如下:

def grad(x, y): #根据上述代码，可知x和y的梯度分别为2x和20y
    return 2 * x, 20 * y
 
def train_SGD():
    cur_x = 40
    cur_y = 20
    lr = 0.096
    track_x = [cur_x] #记录x每次的值
    track_y = [cur_y] #记录y每次的值
    for i in range(10): #作为demo，这里只训练10次
        grad_x, grad_y = grad(cur_x, cur_y) #等效于神经网络的反向传播，求取各参数的梯度
        cur_x -= lr * grad_x
        cur_y -= lr * grad_y
        track_x.append(cur_x)
        track_y.append(cur_y)
    #print(track_x)
    #print(track_y)
    return track_x, track_y
 
def train_RMSProp():
    cur_x = 40
    cur_y = 20
    lr = 3
    r_x, r_y = 0, 0 #伪代码中的r
    alpha = 0.9
    eps = 1e-06
    track_x = [cur_x]
    track_y = [cur_y]
    for i in range(10):
        grad_x, grad_y = grad(cur_x, cur_y)
        r_x = alpha * r_x + (1 - alpha) * (grad_x * grad_x)
        r_y = alpha * r_y + (1 - alpha) * (grad_y * grad_y)
        cur_x -= (grad_x / (np.sqrt(r_x) + eps)) * lr
        cur_y -= (grad_y / (np.sqrt(r_y) + eps)) * lr
        track_x.append(cur_x)
        track_y.append(cur_y)
    #print(track_x)
    #print(track_y)
    return track_x, track_y
 
def paint_tracks(track_x1, track_y1, track_x2, track_y2):
    x = np.linspace(-50, 50, 100)
    y = np.linspace(-50, 50, 100)
    
    X, Y = np.meshgrid(x, y)
    Z = func(X, Y)
 
    fig = plt.figure(figsize=(10, 10))
    ax = Axes3D(fig)
    plt.xlabel('x')
    plt.ylabel('y')
 
    #ax.plot(track_x, track_y, func(np.array(track_x), np.array(track_y)), 'r--')
    tx1, ty1 = track_x1[0], track_y1[0]
    for i in range(1, len(track_x1)):
        tx2, ty2 = track_x1[i], track_y1[i]
        tx = np.linspace(tx1, tx2, 100)
        ty = np.linspace(ty1, ty2, 100)
        ax.plot(tx, ty, func(tx, ty), 'r-')
        tx1, ty1 = tx2, ty2
    ax.scatter(track_x1, track_y1, func(np.array(track_x1), np.array(track_y1)), s=50, c='r')
 
    tx1, ty1 = track_x2[0], track_y2[0]
    for i in range(1, len(track_x2)):
        tx2, ty2 = track_x2[i], track_y2[i]
        tx = np.linspace(tx1, tx2, 100)
        ty = np.linspace(ty1, ty2, 100)
        ax.plot(tx, ty, func(tx, ty), 'b-')
        tx1, ty1 = tx2, ty2
    ax.scatter(track_x2, track_y2, func(np.array(track_x2), np.array(track_y2)), s=50, c='b')
    #ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
    plt.show()
 
track_x_sgd, track_y_sgd = train_SGD()
#paint_track(track_x_sgd, track_y_sgd)
 
track_x_rms, track_y_rms = train_RMSProp()
paint_tracks(track_x_sgd, track_y_sgd, track_x_rms, track_y_rms)

三、RMSProp参数

接下来看下pytorch中的RMSProp优化器，函数原型如下，其中最后三个参数和RMSProp并无直接关系。

torch.optim.RMSprop(params,
                    lr=0.01,
                    alpha=0.99,
                    eps=1e-08,
                    weight_decay=0,
                    momentum=0,
                    centered=False)

• params
  模型里需要被更新的可学习参数，即上文的x和y。

• lr
  学习率。

• alpha
  平滑常数。

• eps
  ε，加在分母上防止除0

• weight_decay
  weight_decay的作用是用当前可学习参数p的值修改偏导数，即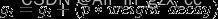：，这里待更新的可学习参数p的偏导数就是。
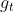  weight_decay的作用是正则化，和RMSProp并无直接关系。

• momentum
  根据上文伪代码第8行，计算出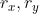后，如果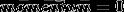，则继续后面的计算，即。
  否则计算过程变成，其中初始为0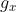，是x的梯度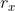，是上述累计的x的梯度的平方。

momentum和RMSProp并无直接关系。

• centered
  如果centerd为False，则按照上述伪代码计算，即分母是。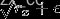
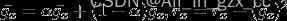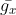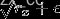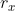  否则计算过程变成，这里初始为0，然后分母依然是，但是不一样了。

centered和RMSProp并无直接关系，是为了让结果更平稳。