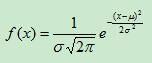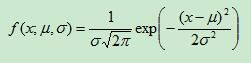python正态分布_Python数据可视化实现正态分布（高斯分布）

正态分布（Normal distribution）又成为高斯分布（Gaussian distribution）

若随机变量X服从一个数学期望为

、标准方差为

的高斯分布，记为：

则其概率密度函数为：

正态分布的期望值

决定了其位置，其标准差

决定了分布的幅度。因其曲线呈钟形，因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是

的正态分布：

概率密度函数

代码实现：

# Python实现正态分布

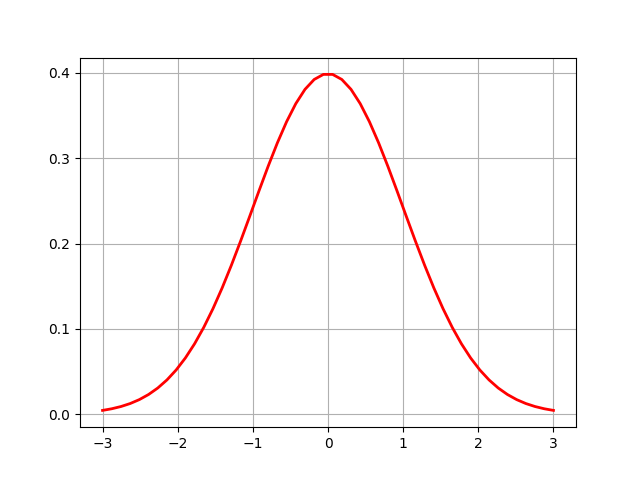
# 绘制正态分布概率密度函数

u = 0 # 均值μ

u01 = -2

sig = math.sqrt(0.2) # 标准差δ

sig01 = math.sqrt(1)

sig02 = math.sqrt(5)

sig_u01 = math.sqrt(0.5)

x = np.linspace(u - 3*sig, u + 3*sig, 50)

x_01 = np.linspace(u - 6 * sig, u + 6 * sig, 50)

x_02 = np.linspace(u - 10 * sig, u + 10 * sig, 50)

x_u01 = np.linspace(u - 10 * sig, u + 1 * sig, 50)

y_sig = np.exp(-(x - u) ** 2 /(2* sig **2))/(math.sqrt(2*math.pi)*sig)

y_sig01 = np.exp(-(x_01 - u) ** 2 /(2* sig01 **2))/(math.sqrt(2*math.pi)*sig01)

y_sig02 = np.exp(-(x_02 - u) ** 2 / (2 * sig02 ** 2)) / (math.sqrt(2 * math.pi) * sig02)

y_sig_u01 = np.exp(-(x_u01 - u01) ** 2 / (2 * sig_u01 ** 2)) / (math.sqrt(2 * math.pi) * sig_u01)

plt.plot(x, y_sig, "r-", linewidth=2)

plt.plot(x_01, y_sig01, "g-", linewidth=2)

plt.plot(x_02, y_sig02, "b-", linewidth=2)

plt.plot(x_u01, y_sig_u01, "m-", linewidth=2)

# plt.plot(x, y, 'r-', x, y, 'go', linewidth=2,markersize=8)

plt.grid(True)

plt.show()

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持谷谷点程序。