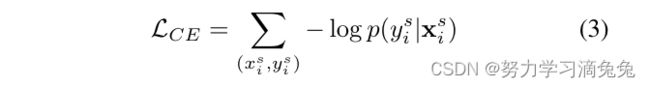【开集识别论文解读】Few-Shot Open-Set Recognition using Meta-Learning——CVPR2020

论文原文：https://arxiv.org/abs/2005.13713

本文介绍了一种新的开集元学习算法（PEELER）算法，实验结果表明，PEELER在小样本和大规模识别方面都达到了最先进的开放集识别性能。

1. Introduction

开集识别目前主要的研究是在大规模环境中，使用基于大规模分类器的解决方案。这些尝试通过后处理后验类分布来识别新类，定义一个“拒绝”类，该类使用人工生成的示例或从训练类中采样的示例，或两者的组合进行训练。本文试图将开集识别推广到大规模环境之外：大规模和小样本识别。主要有三个原因：首先，在所有设置下，开集识别都是一个挑战。其次，由于标记数据的稀缺性，小样本开集识别比大规模开集识别更难解决。第三，与开集识别一样，小样本识别的主要挑战是对训练期间看不到的数据做出准确的决策。由于这使得稳健性成为少数快照体系结构的主要特征，因此这些体系结构可能也擅长于开放集识别。

在这项工作中，研究了小样本问题的一类流行解决方案的开集性能，称为元学习（ML）。ML方法用情景训练取代了传统的小批量CNN训练。通过对每个类的一个子集和一个子集示例进行随机抽样，生成一个支持和查询集，并对其应用分类损失。这将使分类任务随机化，在每个ML步骤中对嵌入进行优化，从而生成更健壮的嵌入，减少对任何特定类集的过度拟合。我们将这个想法推广到开集识别，通过在每集中随机选择一组新类，并引入一个损失，使这些类的示例的后验熵最大化。这迫使嵌入更好地解释看不见的类，在目标类区域之外产生高熵后验分布。此解决方案至少有两大好处。首先，因为它利用了最先进的方法来进行小样本学习，所以它立即将开集识别扩展到小样本问题。其次，由于ML嵌入是鲁棒的，而开集识别是泛化的，因此即使在大规模环境中，后者的性能也会提高。本文还研究了特征空间中使用的度量对开集识别性能的作用，表明特定形式的马氏距离比常用的欧几里德距离具有显著的增益。

本文的贡献如下：

• 一种新的基于ML的开集识别公式。将开集识别推广到小样本。
• 将交叉熵损失和一种新的开集损失相结合，以提高开集在大规模和小样本环境下的性能
• 一种基于高斯嵌入的ML开集识别算法。

2. Related Work

开集识别：开集识别解决的是一种测试时可能面对来自训练过程中看不到的类的样本的问题场景，目标是赋予开集分类器拒绝此类样本的机制。最早的深度学习方法之一是Scheirer等人的工作，该工作为分类器生成的Logit提出了一种极值参数再分配方法。后来的工作在分类模型或生成模型中考虑了这个问题。Schlachter等人提出了一种类内分割方法，其中使用闭集分类器将数据分割为典型和非典型子集，将开放集识别重新表述为一个传统的分类问题。G-OpenMax利用一个经过训练的生成器，从一个表示所有未知类的额外类中合成示例。Neal等人引入了反事实图像生成，其目的是生成无法分类到任何可见类的样本，为分类器训练生成额外的类。
所有这些方法都将看不见的类集减少为一个额外的类。虽然开放样本可以从不同类别中提取，并且具有显著的视觉差异，但他们假设特征提取器可以将它们全部映射到单个特征空间簇中。虽然理论上可能，但这很困难。相反，我们允许按可见类进行聚类，并将不属于这些集群的样本标记为不可见。我们相信这是一种更自然的方法来检测看不见的类。

分布外检测：与开集识别类似的问题是检测分布外（OOD）检测。通常，这是从不同的数据集检测样本，即不同于用于训练模型的分布。虽然[9]通过直接使用softmax分数解决了这个问题，但后来的工作通过提高可靠性来改进结果。这个问题不同于开集识别，因为OOD样本不一定来自看不见的类。例如，它们可能是seen类样本的扰动版本，这在对抗性攻击文献中很常见。唯一的限制是它们不属于训练分布。通常，这些样本比不可见类的样本更容易检测。在文献中，它们往往是来自其他数据集的类，甚至是噪声图像。这与开集识别不同，在开集识别中，看不见的类往往来自同一个数据集。

小样本学习：近年来出现了关于少镜头学习的广泛研究。这些方法大致可分为两个分支：基于优化和基于度量的方法。基于优化的方法通过展开反向传播过程来处理泛化问题。具体而言，Ravi等人提出了一个学习者模块，该模块经过培训可以更新到新任务。MAML及其变体提出了一种训练程序，其中参数根据二级梯度计算的损失进行更新。基于度量的方法试图比较支持样本和查询样本之间的特征相似度。Vinyals等人引入了片段训练的概念，其中训练程序旨在模拟测试阶段，该阶段与余弦距离一起用于训练循环网络。原型网络通过结合度量学习和交叉熵损失，引入了从支持集特征构建的类原型。关系网络利用神经网络隐式地探索了一对支持和查询特征之间的关系，而不是直接在特征空间上构建度量。

3. Classification tasks and meta Learning

在本节中，讨论了不同的分类设置和元学习，为在大规模和小样本设置下提出的开集识别解决方案提供基础。

3.1 Classification settings

Softmax classification

最常用的对象识别和图像分类深度学习架构是softmax分类器。这包括映射图像的嵌入到特征向量，由多个神经网络层实现，softmax层具有线性映射，用于估计类后验概率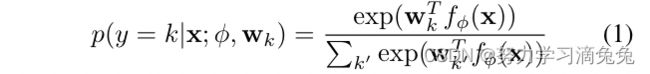

 其中表示所有嵌入参数，是一组分类器权重向量。最近的工作将度量学习与softmax分类相结合，使用距离函数实现softmax层

式中，。softmax分类器通过训练集学习，其中 是一组训练图像的类，是训练示例的数量。这包括找到使交叉熵损失最小化的分类器和嵌入参数 

在测试集上评估识别性能，其中，, 是一组测试类，是测试示例数。 

Closed vs. open set classification

闭集分类：训练集和测试集是相同的，即。

开集分类：，在这种情况下，中的类别表示为（训练期间）可见类，中的类别表示为不可见类。

Large-scale vs few-shot recognition

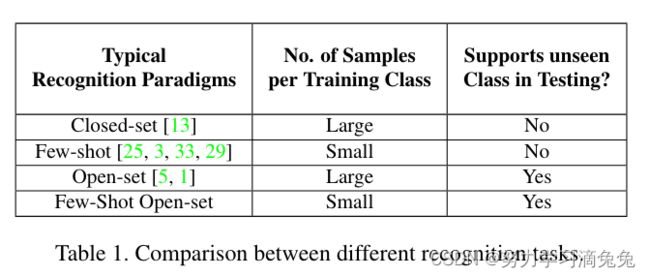
在大规模识别环境中，训练示例的数量非常多，对于像ImageNet这样的数据集，达到数百万。相反，对于小样本识别，这个数字非常小，通常每个类少于20个示例。每个类有K个训练示例的小样本问题通常称为K-shot识别。请注意，测试示例的数量在区分这两种设置方面没有任何作用。由于这些示例仅用于性能评估，因此测试集在这两种设置下应具有相同的基数。如表1所示，训练数据的规模和覆盖范围中的不同属性组合定义了不同的分类范式。在文献和本文的重点中，很少有小样本开放集设置的探索。

3.2 Meta-learning

 元学习（ML）解决“学会学习”的问题。元学习者依赖于元训练集，其中是第个学习问题的训练和测试集，是用于训练的学习问题的数量；元测试集，其中是第个测试学习问题的训练和测试集，是用于测试的学习问题的数量。给定，元学习者学习如何将一对映射到利用优化求解的算法中。

具体流程：在元迭代中，元模型用前一个元迭代生成的元模型初始化。然后执行两个步骤。首先，元学习算法执行映射

为训练集生成最优模型的估计。然后使用测试集查找模型 

对于适当的损失函数L，例如交叉熵，使用适当的优化程序，例如反向传播。结果 最终作为元迭代的最佳元模型返回。在测试期间，最终元模型 元学习者使用元测试集中的训练集生成新模型

并用评估其性能。

 ML for few-shot recognition.

 在本文中，采用了流行的原型网络体系结构。在这种情况下，ML主要是一种随机化过程。元训练集MS是通过对训练和测试类进行采样生成的。模型是公式（2）的softmax分类器，元学习映射实现了高斯平均极大似然估计

Benefits of ML for open-set classification. 

ML程序与用于训练softmax分类器的标准小批量程序非常相似。除了使用片段训练而不是更流行的小批量训练外，还有两个主要区别。首先，通过而不是中的示例的反向传播来更新。其次，将所有类中随机示例的小批量替换为和中包含的N个类的子集中的示例。将每个set学习的分类任务随机化，迫使嵌入更好地推广到看不见的数据。这种特性使ML成为小样本学习的一个很好的解决方案，因为训练数据缺乏对类内变化的良好覆盖。在这种情况下，在训练期间，将看不到来自已知类的大量测试样本子集。同样的属性使ML成为开集分类的一个很好的候选者，根据定义，分类器必须处理来自不可见类的不可见样本。

4. Meta Learning-based open-set recognition 

4.1. Open-Set Meta-Learning

如图1所示，开放集元学习（PEELER）依赖于元训练集，元测试集。与标准ML相比，唯一的区别是集是开放集。虽然训练集S与标准ML中使用的训练集S相同，但测试集T增加了看不见的类。当ML步骤保持如（4）所示时，（5）的优化步骤变为

其中，是的可见（不可见）类集合，是应用于已知类的分类损失（通常为交叉熵损失），是应用于中未看到类的开集损失。 

Few-shot open-set recognition.

小样本设置需要对构成支持集和查询集的类进行采样。与闭集小样本识别类似，第i集的支持集是通过对N个类和每个类的K个示例进行采样获得的。这定义了已知类。但是，查询集是由这些类与M个额外的不可见类组合而成的。这些支持和查询集在（8）中使用。

Large-scale open-set recognition.

在大规模环境中，可见类有大量的示例，并且经过良好的训练，无需重新采样。然而，对不可见的类进行重采样仍然是有利的，因为它可以使嵌入更好地泛化到这些类。在每一个set中，从类标签空间中随机抽取M个类，形成一组不可见的类，其余的类作为可见的类使用。没有支持集，就不再需要（4）的元学习步骤。相反，依赖一组可见类来调整模型，使其仅将样本分类到这些类中，即映射

损失函数（8）仍然适用。

Open-set loss. 

在推理过程中，当面对来自不可见的类的样本时，模型不应将很大的概率分配给任何类。在这种情况下，如果所见类别中的最大类别概率很小，则可以拒绝样本。为了实现这一点，学习算法应该最小化样本在可见类上的概率。这可以通过最大化所见类概率的熵来实现，即使用负熵作为损失函数。

4.2 Gaussian Embedding

 虽然PEELER是一个通用框架，但在这项工作中提出了一个基于原型网络架构的实现方案。首先定义一组类原型，并将与最近的类原型有较大距离的样本分配给这组看不见的类。对于低级分类，类原型是（7）的类平均值。对于大规模分类，假设嵌入在网络中并通过反向传播学习的固定原型。

原型网络通常使用欧几里德距离来实现，即：

这意味着每一类的特征都遵循均值和对角协方差的高斯分布，其中由所有类共享。虽然对于闭集小样本学习是合理的，但当引入开集样本时，这可能是非常不理想的。图2说明了具有三个可见类和两个不可见类的设置的问题。尽管如图2（a）所示，嵌入使得所看到的类呈球形分布并具有相同的协方差，但在训练期间看不到的开放集样本仍然以随机位置嵌入到特征空间中。因此，尽管图2（b）中所示的闭集分类器的最佳边界与图2（c）中所示的距离的轮廓相匹配，但对于开集识别来说，它们并不是最佳的。事实上，如图2（d）所示，可见类和不可见类之间的最佳边界形状甚至可能因类而异。 

为了说明这一点，本文假设k类的平均值和协方差为高斯分布。因此，欧几里德距离（11）被马氏距离取代 

为了保持参数数量可控，假设所有协方差矩阵都是对角的，即，精度矩阵用于简化计算。与类原型类似，精度矩阵的学习取决于识别设置。对于大规模开集识别，是通过反向传播直接学习的网络参数。在小样本设置下，在支持样本可用的情况下，我们引入了一个新的嵌入函数和可学习参数，并定义了

 

5. Experiments 

将该方法与最新的开放集识别方法（SOTA）进行了比较。继Neal等人之后，我们评估了分类精度和开放集检测性能。所有的训练都是基于封闭集合类的训练样本。对于测试，我们使用来自训练和开放集类的测试样本。分类精度用于衡量模型对封闭集样本（即来自封闭集类的测试样本）的分类程度。AUROC（ROC曲线下面积）度量用于衡量模型在所有测试样本中检测开放集样本（即来自开放集类的测试样本）的程度。

5.1 Large-Scale Open-Set Recognition

以往大多数关于开集识别的工作都是针对大规模环境而设计的。在这里，评估了CIFAR10和扩展miniImageNet上的PEELER。CIFAR10由10个类的60000个图像组成。首先随机选择6个类作为闭集类，其他4个类作为开集类。结果在闭/开集类的5个随机分区上求平均值。扩展的miniImageNet是为小样本学习而设计的。我们使用64个训练类别和每个类别600张图像作为闭集训练数据，而每个类别的300张额外图像用于闭集测试。来自20个测试类别的图像用于开放集测试。

训练在CIFAR10上，从每个set的6个闭集类中随机抽取2个样本以应用开集损失，其余4个类用于训练分类。在miniImageNet上，闭集/开集分区是固定的。

Baseline：OpenMax、G-OpenMax和Counterfact，以及分布外SOTA方法，Confidence。

5.2. Few-Shot Open-Set Recognition

 数据集。mini Imagenet，64类用于训练，16类用于验证，20类用于测试。

训练开放集问题遵循5-way小样本识别设置。在训练过程中，每个set从训练集中随机选择10个类，5个类作为封闭集，另5个类作为不可见类。所有支持集样本都来自闭集类。查询集包含来自封闭集类的样本，以及来自开放集类的样本。使用相同的策略从测试集中抽取评估集。评估重复600次，以尽量减少不确定性。

Baseline：GaussianE + OpenMax， GaussianE + Counterfactual