python-opencv图像处理之哈里斯角检测
- 理解什么是特征,为什么拐角重要等等
- 我们将了解"Harris Corner Detection”背后的概念。
- 我们将看到以下函数:cv.cornerHarris(),cv.cornerSubPix()
1.我们不妨先看一下下面这张图片:
图像非常简单。在图像的顶部,给出了六个小图像块。你的问题是在原始图像中找到这些补丁的确切位置。你可以找到多少正确的结果?
A和B是平坦的表面,它们散布在很多区域上。很难找到这些补丁的确切位置。
C和D更简单。它们是建筑物的边缘。你可以找到一个大概的位置,但是准确的位置仍然很困难。这是因为沿着边缘的每个地方的图案都是相同的。但是,在边缘,情况有所不同。因此,与平坦区域相比,边缘是更好的特征,但不够好(在拼图游戏中比较边缘的连续性很好)。
最后,E和F是建筑物的某些角落。而且很容易找到它们。因为在拐角处,无论将此修补程序移动到何处,它的外观都将有所不同。因此,它们可以被视为很好的特征。
我们在图像中找到了特征。找到它之后,你应该能够在其他图像中找到相同的图像。怎么做?我们围绕该特征采取一个区域,我们用自己的语言解释它,例如“上部是蓝天,下部是建筑物的区域,在建筑物上有玻璃等”,而你在另一个建筑物中搜索相同的区域图片。基本上,你是在描述特征。同样,计算机还应该描述特征周围的区域,以便可以在其他图像中找到它。所谓的描述称为特征描述。获得特征及其描述后,你可以在所有图像中找到相同的功能并将它们对齐,缝合在一起或进行所需的操作。
2.我们看到角是图像中各个方向上强度变化很大的区域。Chris Harris和Mike Stephens在1988年的论文《组合式拐角和边缘检测器》中做了一次尝试找到这些拐角的尝试,所以现在将其称为哈里斯拐角检测器。他把这个简单的想法变成了数学形式。它基本上找到了 ( u , v ) (u,v) (u,v)在所有方向上位移的强度差异。表示如下:
E ( u , v ) = ∑ x , y w ( x , y ) ⏟ window function [ I ( x + u , y + v ) ⏟ shifted intensity − I ( x , y ) ⏟ intensity ] 2 E(u,v) = \sum_{x,y} \underbrace{w(x,y)}\text{window function} \, [\underbrace{I(x+u,y+v)}\text{shifted intensity}-\underbrace{I(x,y)}_\text{intensity}]^2 E(u,v)=x,y∑ w(x,y)window function[ I(x+u,y+v)shifted intensity−intensity I(x,y)]2
窗口函数要么是一个矩形窗口,要么是高斯窗口,它在下面赋予了值。
我们必须最大化这个函数 E ( u , v ) E(u,v) E(u,v)用于角检测。这意味着,我们必须最大化第二个项。将泰勒扩展应用于上述方程,并使用一些数学步骤(请参考任何你喜欢的标准文本书),我们得到最后的等式:
E ( u , v ) ≈ [ u v ] M [ u v ] E(u,v) \approx \begin{bmatrix} u & v \end{bmatrix} M \begin{bmatrix} u \ v \end{bmatrix} E(u,v)≈[uv]M[u v]
其中
M = ∑ x , y w ( x , y ) [ I x I x I x I y I x I y I y I y ] M = \sum_{x,y} w(x,y) \begin{bmatrix}I_x I_x & I_x I_y \ I_x I_y & I_y I_y \end{bmatrix} M=x,y∑w(x,y)[IxIxIxIy IxIyIyIy]
在此, I x I_x Ix和 I y I_y Iy分别是在x和y方向上的图像导数。(可以使用cv.Sobel()轻松找到)。
然后是主要部分。之后,他们创建了一个分数,基本上是一个等式,它将确定一个窗口是否可以包含一个角。
R = d e t ( M ) − k ( t r a c e ( M ) ) 2 R = det(M) - k(trace(M))^2 R=det(M)−k(trace(M))2
其中
d e t ( M ) = λ 1 λ 2 det(M)=\lambda_1\lambda_2 det(M)=λ1λ2
t r a c e ( M ) = λ 1 + λ 2 trace(M)=\lambda_1+\lambda_2 trace(M)=λ1+λ2
λ 1 \lambda_1 λ1 and λ 2 \lambda_2 λ2 是 M M M 的特征值
因此,这些特征值的值决定了区域是拐角,边缘还是平坦。
当 ∣ R ∣ |R| ∣R∣较小,这在 λ 1 \lambda_1 λ1和 λ 2 \lambda_2 λ2较小时发生,该区域平坦。
当 R < 0 R<0 R<0时(当 λ 1 > > λ 2 \lambda_1 >>\lambda_2 λ1>>λ2时发生,反之亦然),该区域为边。
当 R R R很大时,这发生在 λ 1 \lambda_1 λ1和 λ 2 \lambda_2 λ2大且 λ 1 \lambda_1 λ1~ λ 2 \lambda_2 λ2时,该区域是角。
可以用如下图来表示:
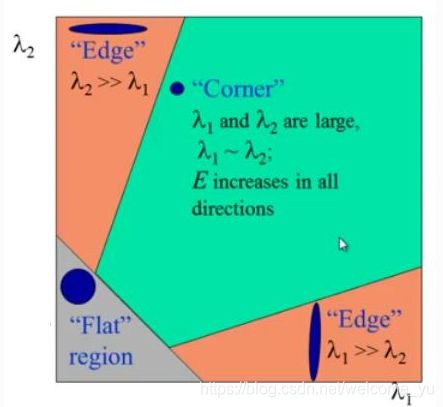
因此,Harris Corner Detection的结果是具有这些分数的灰度图像。合适的阈值可为您提供图像的各个角落。我们将以一个简单的图像来完成它。
OpenCV中的哈里斯角检测
为此,OpenCV具有函数cv.cornerHarris()。其参数为: - img - 输入图像,应为灰度和float32类型。 - blockSize - 是拐角检测考虑的邻域大小 - ksize - 使用的Sobel导数的光圈参数。 - k - 等式中的哈里斯检测器自由参数。
请参阅以下示例:
`import numpy as np
import cv2 as cv
filename = 'chessboard.png'
img = cv.imread(filename)
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
gray = np.float32(gray)
dst = cv.cornerHarris(gray,2,3,0.04)
#result用于标记角点,并不重要
dst = cv.dilate(dst,None)
#最佳值的阈值,它可能因图像而异。
img[dst>0.01*dst.max()]=[0,0,255]
cv.imshow('dst',img)
if cv.waitKey(0) & 0xff == 27:
cv.destroyAllWindows()`