【建模算法】Python调用Gurobi求解TSP问题

【建模算法】Python调用Gurobi求解TSP问题

TSP (traveling salesman problem，旅行商问题)是典型的NP完全问题，即其最坏情况下的时间复杂度随着问题规模的增大按指数方式增长，到目前为止还未找到一个多项式时间的有效算法。本文探讨了Python调用Gurobi优化器求解TSP问题。

一、问题描述

​ 本案例以31个城市为例，假定31个城市的位置坐标如表1所列。寻找出一条最短的遍历31个城市的路径。

城市编号	X坐标	Y坐标	城市编号	X坐标	Y坐标
1	1.304	2.312	17	3.918	2.179
2	3.639	1.315	18	4.061	2.37
3	4.177	2.244	19	3.78	2.212
4	3.712	1.399	20	3.676	2.578
5	3.488	1.535	21	4.029	2.838
6	3.326	1.556	22	4.263	2.931
7	3.238	1.229	23	3.429	1.908
8	4.196	1.044	24	3.507	2.376
9	4.312	0.79	25	3.394	2.643
10	4.386	0.57	26	3.439	3.201
11	3.007	1.97	27	2.935	3.24
12	2.562	1.756	28	3.14	3.55
13	2.788	1.491	29	2.545	2.357
14	2.381	1.676	30	2.778	2.826
15	1.332	0.695	31	2.37	2.975
16	3.715	1.678

二、Gurobi 求解器简介

Gurobi 是全球综合能力排名靠前的数学规划求解器。目前最新版本 9.5.1，可以求解的问题类型包括：

（1）线性约束和目标模型（连续变量、混合整数）

（2）二阶锥模型 （连续变量、混合整数）

（3）二次凸约束和目标模型（连续变量、混合整数）

（4）二次非凸（双线性、二次等式约束等）约束和目标模型（连续变量、混合整数）

（5）非线性模型（除式、高阶多项式、指数、对数、三角函数、范数等）（连续变量、混合整数）

对于以上模型，可以叠加的功能包括但不限于：

（1）约束和目标中带有 最大、最小、绝对值等数学函数，或者带有 AND、OR、INDICATOR 逻辑条件的模型 （连续变量、混合整数）

（2）多目标优化

（3）需要获得部分或者全部可行解或者最优解的模型

（4）不可行或者无界分析

（5）优化参数自动调优功能

（6）分布式计算或者多线程计算

更多Gurobi 功能参见 http://www.gurobi.cn/

三、TSP问题的数学模型

假设$d_{ij}$为第i个城市与第j个城市之间的距离，num为城市数，$x_{ij}$为第i个城市与第j个城市之间的决策变量，此为0-1变量，0代表第i个城市与第j个城市之间不相连、1代表第i个城市与第j个城市之间相连。

要建立的目标为经过所有城市距离最短，约束条件为每个城市只经过一次。可以建立如下模型：

$min\sum _{i=1}^{num}\sum _{j=1}^{num}{x}_{ij}{d}_{ij}$

s.t.

$\sum _{i=1}^{num}{x}_{ij}=1$ j=1,2,…,num

$\sum _{j=1}^{num}{x}_{ij}=1$ i=1,2,…,num

$u_i-u_j+num\times x_{ij}\le n-1$ $1<i\ne j\le num$

$x_{ij}$为0或1，$u_i$为实数。约束条件前两个就是保证每个城市只去一次，最后一个约束条件即为防止子回路的出现。

四、python调用Gurobi优化器求解TSP问题的步骤

安装gurobi可以自行网上找教程，此处不再赘述。

• 导入包

from gurobipy import *
import numpy as np

• 创建模型

model=Model("question1")

• 定义变量,计算矩阵

vtype=GRB.BINARY 二进制变量，0-1变量

vtype=GRB.CONTINUOUS 连续变量

vtype=GRB.INTEGER 整数变量

lb 是变量下限，ub是变量上限

在这个问题中，$x_{ij}$为31__31的矩阵0-1变量，$u_i$为311的实数变量。

sdpvar实型变量，intvar 整型变量 binvar 0-1型变量

对于此问题的变量可以定义为：

#读取31座城市坐标
coord = []
with open("data.txt", "r") as lines:
    lines = lines.readlines()
for line in lines:
    xy = line.split()
    coord.append(xy)
coord = np.array(coord)
w, h = coord.shape
coordinates = np.zeros((w, h), float)
for i in range(w):
    for j in range(h):
        coordinates[i, j] = float(coord[i, j])

# x点坐标
data_x=coordinates[:,0]
# y点坐标
data_y=coordinates[:,1]

data_num=len(data_x)
distance_juzheng=np.zeros((data_num,data_num))

for i in range(0,data_num):
    for j in range(0,data_num):
        if (i==j):
            distance_juzheng[i,j]=100000
        else:
            distance_juzheng[i,j]=np.sqrt(np.square((data_x[i]-data_x[j]))+np.square((data_y[i]-data_y[j])))

#定义变量
x=model.addMVar((data_num,data_num),lb=0,ub=1,vtype=GRB.BINARY)  #lb变量下限， ub变量上限 
u=model.addMVar((data_num),vtype=GRB.CONTINUOUS)  #lb变量下限， ub变量上限 

• 目标函数

  $min\sum _{i=1}^{num}\sum _{j=1}^{num}{x}_{ij}{d}_{ij}$

#构造目标函数
objsum=[]
for i in range(0,data_num):  
    for j in range(0,data_num):  
        objsum=objsum+x[i,j]*distance_juzheng[i,j]

model.setObjective(objsum,GRB.MINIMIZE)

• 约束条件

#构造约束条件
for i in range(0,data_num):  
    constrsum=sum(x[i,:])
    model.addConstr(constrsum==1)

for j in range(0,data_num):  
    constrsum1=sum(x[:,j])
    model.addConstr(constrsum1==1)

for i in range(1,data_num):  
    for j in range(1,data_num): 
        if(i!=j):
            model.addConstr((u[i]-u[j]+data_num*x[i,j])<=data_num-1)

• 优化求解

model.optimize()

五、求解结果

最优路径：
1-> 15-> 14-> 12-> 13-> 7-> 10-> 9-> 8-> 2-> 4-> 16-> 5-> 6-> 11-> 23-> 19-> 17-> 3-> 18-> 22-> 21-> 20-> 24-> 25-> 26-> 28-> 27-> 30-> 31-> 29-> 1

轨迹图：

完整代码

#求解31座城市的TSP问题完整代码

from gurobipy import *
import numpy as np

model=Model("question1")

#读取31座城市坐标
coord = []
with open("data.txt", "r") as lines:
    lines = lines.readlines()
for line in lines:
    xy = line.split()
    coord.append(xy)
coord = np.array(coord)
w, h = coord.shape
coordinates = np.zeros((w, h), float)
for i in range(w):
    for j in range(h):
        coordinates[i, j] = float(coord[i, j])
        
# x点坐标
data_x=coordinates[:,0]
# y点坐标
data_y=coordinates[:,1]

data_num=len(data_x)
distance_juzheng=np.zeros((data_num,data_num))

for i in range(0,data_num):
    for j in range(0,data_num):
        if (i==j):
            distance_juzheng[i,j]=100000
        else:
            distance_juzheng[i,j]=np.sqrt(np.square((data_x[i]-data_x[j]))+np.square((data_y[i]-data_y[j])))

#定义变量
x=model.addMVar((data_num,data_num),lb=0,ub=1,vtype=GRB.BINARY)  #lb变量下限， ub变量上限 
u=model.addMVar((data_num),vtype=GRB.CONTINUOUS)  #lb变量下限， ub变量上限 

#构造目标函数
objsum=[]
for i in range(0,data_num):  
    for j in range(0,data_num):  
        objsum=objsum+x[i,j]*distance_juzheng[i,j]

model.setObjective(objsum,GRB.MINIMIZE)


 #构造约束条件
for i in range(0,data_num):  
    constrsum=sum(x[i,:])
    model.addConstr(constrsum==1)

for j in range(0,data_num):  
    constrsum1=sum(x[:,j])
    model.addConstr(constrsum1==1)

for i in range(1,data_num):  
    for j in range(1,data_num): 
        if(i!=j):
            model.addConstr((u[i]-u[j]+data_num*x[i,j])<=data_num-1)

model.optimize()
best=(x.X).astype(int)
print(f"最优目标值为：{model.ObjVal}")
print(f"最优分配为：{best}")

运行结果：

Gurobi Optimizer version 9.5.1 build v9.5.1rc2 (win64)
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 932 rows, 992 columns and 4532 nonzeros
Model fingerprint: 0xbe4e71f7
Variable types: 31 continuous, 961 integer (961 binary)
Coefficient statistics:
  Matrix range     [1e+00, 3e+01]
  Objective range  [1e-01, 1e+05]
  Bounds range     [1e+00, 1e+00]
  RHS range        [1e+00, 3e+01]
Presolve removed 0 rows and 1 columns
Presolve time: 0.02s
Presolved: 932 rows, 991 columns, 4532 nonzeros
Variable types: 30 continuous, 961 integer (961 binary)
Found heuristic solution: objective 2900002.5107

Root relaxation: objective 1.242587e+01, 107 iterations, 0.00 seconds (0.00 work units)

    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

     0     0   12.42587    0   45 2900002.51   12.42587   100%     -    0s
H    0     0                    2900002.4836   12.42587   100%     -    0s
H    0     0                    2800004.9958   12.42587   100%     -    0s
     0     0   13.38934    0   65 2800005.00   13.38934   100%     -    0s
     0     0   13.52139    0   61 2800005.00   13.52139   100%     -    0s
     0     0   13.52274    0   69 2800005.00   13.52274   100%     -    0s
     0     0   13.52282    0   68 2800005.00   13.52282   100%     -    0s
     0     0   14.53402    0   59 2800005.00   14.53402   100%     -    0s
H    0     0                    1800012.4470   14.53402   100%     -    0s
     0     0   14.64368    0   60 1800012.45   14.64368   100%     -    0s
     0     0   14.64368    0   60 1800012.45   14.64368   100%     -    0s
     0     0   14.64882    0   62 1800012.45   14.64882   100%     -    0s
     0     0   14.65151    0   61 1800012.45   14.65151   100%     -    0s
H    0     0                    1600012.0222   14.65151   100%     -    0s
     0     0   14.65956    0   59 1600012.02   14.65956   100%     -    0s
H    0     0                    1100028.0719   14.65956   100%     -    0s
     0     0   14.65956    0   59 1100028.07   14.65956   100%     -    0s
     0     0   14.65956    0   59 1100028.07   14.65956   100%     -    0s
     0     0   14.65956    0   51 1100028.07   14.65956   100%     -    0s
H    0     0                      16.2382171   14.65956  9.72%     -    0s
     0     0   14.66899    0   45   16.23822   14.66899  9.66%     -    0s
     0     0   14.66899    0   54   16.23822   14.66899  9.66%     -    0s
     0     0   14.66899    0   61   16.23822   14.66899  9.66%     -    0s
     0     0   14.66899    0   61   16.23822   14.66899  9.66%     -    0s
     0     0   14.66899    0   59   16.23822   14.66899  9.66%     -    0s
     0     0   14.66899    0   59   16.23822   14.66899  9.66%     -    0s
     0     0   14.66899    0   59   16.23822   14.66899  9.66%     -    0s
H    0     0                      15.7186599   14.66899  6.68%     -    0s
     0     0   14.66899    0   51   15.71866   14.66899  6.68%     -    0s
     0     0   14.66899    0   51   15.71866   14.66899  6.68%     -    0s
     0     0   14.66899    0   51   15.71866   14.66899  6.68%     -    0s
     0     0   14.66899    0   51   15.71866   14.66899  6.68%     -    0s
     0     0   14.66899    0   51   15.71866   14.66899  6.68%     -    0s
     0     0   14.66899    0   51   15.71866   14.66899  6.68%     -    0s
     0     0   14.66899    0   45   15.71866   14.66899  6.68%     -    0s
     0     0   14.66899    0   61   15.71866   14.66899  6.68%     -    0s
     0     0   14.66899    0   60   15.71866   14.66899  6.68%     -    0s
     0     0   14.66899    0   60   15.71866   14.66899  6.68%     -    0s
     0     0   14.66899    0   58   15.71866   14.66899  6.68%     -    0s
     0     0   14.66899    0   58   15.71866   14.66899  6.68%     -    0s
     0     0   14.66899    0   58   15.71866   14.66899  6.68%     -    0s
     0     0   14.66899    0   58   15.71866   14.66899  6.68%     -    0s
     0     0   14.66899    0   58   15.71866   14.66899  6.68%     -    0s
     0     2   14.66899    0   58   15.71866   14.66899  6.68%     -    0s
H 1628  1026                      15.7186599   14.73997  6.23%   8.5    2s
*12769  8050              57      15.6996836   14.84307  5.46%   8.4    4s
 13210  8619   14.91088   24   32   15.69968   14.84449  5.45%   8.3    5s
*24056 15401              39      15.6721259   14.87890  5.06%   8.1    6s
*24057 15251              38      15.6493581   14.87890  4.92%   8.1    6s
H29434 17104                      15.4330841   14.89825  3.47%   8.1    7s
*33812 17603              83      15.4105727   14.89825  3.32%   8.6    8s
 44242 20220   15.18573   46   72   15.41057   14.93102  3.11%   8.7   10s
H46430 19702                      15.3874549   14.93102  2.97%   9.0   11s
 58661 22557   15.07210   56   56   15.38745   14.95224  2.83%   9.0   15s
H58816 21525                      15.3825444   14.95224  2.80%   9.0   18s
 67759 24235   15.04976   95   41   15.38254   14.95224  2.80%   9.1   20s
 117683 32944     cutoff  105        15.38254   14.99875  2.49%   9.1   25s
 157428 47324   15.37361   77   28   15.38254   15.03425  2.26%   9.1   30s
 201865 61834     cutoff   67        15.38254   15.06842  2.04%   9.2   35s
 243220 72133   15.26096   66   29   15.38254   15.09487  1.87%   9.3   40s
 279757 78847   15.30388   69   12   15.38254   15.11361  1.75%   9.4   45s
 309860 83532     cutoff   85        15.38254   15.12884  1.65%   9.5   50s
 338190 86252   15.37650   76    6   15.38254   15.14324  1.56%   9.5   55s
 368798 88155     cutoff   95        15.38254   15.15807  1.46%   9.6   60s
 398096 88732   15.25925   71   21   15.38254   15.17184  1.37%   9.6   65s
 426981 87036 infeasible   78        15.38254   15.18432  1.29%   9.6   70s
 456017 84800     cutoff   73        15.38254   15.19700  1.21%   9.7   75s
 483613 82030 infeasible   80        15.38254   15.20841  1.13%   9.7   80s
 509368 77406   15.28221   72   10   15.38254   15.22011  1.06%   9.8   85s
 537451 71269     cutoff   79        15.38254   15.23224  0.98%   9.8   90s
 568470 62502     cutoff   96        15.38254   15.24598  0.89%   9.8   95s
 593492 55036   15.35594   77   17   15.38254   15.25763  0.81%   9.8  100s
 625294 43717   15.32996   88    6   15.38254   15.27493  0.70%   9.8  105s
 656274 30390   15.30927   76    6   15.38254   15.29557  0.57%   9.8  110s
 691398  9606   15.35426   81   18   15.38254   15.33712  0.30%   9.7  115s

Cutting planes:
  Learned: 33
  Gomory: 51
  Cover: 197
  MIR: 35
  Flow cover: 241
  Inf proof: 142
  Zero half: 24

Explored 703817 nodes (6750483 simplex iterations) in 116.41 seconds (158.76 work units)
Thread count was 8 (of 8 available processors)

Solution count 10: 15.3825 15.3875 15.4106 ... 1.10003e+06

Optimal solution found (tolerance 1.00e-04)
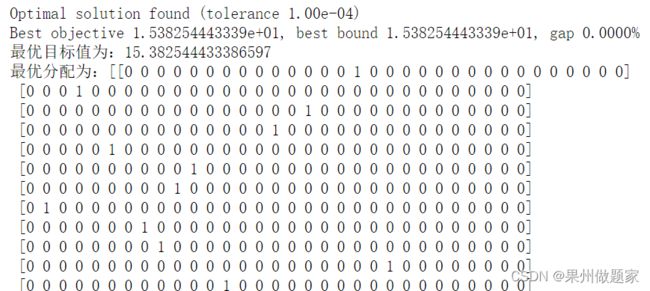
Best objective 1.538254443339e+01, best bound 1.538254443339e+01, gap 0.0000%
最优目标值为：15.382544433386597
最优分配为：[[0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]
 [1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0]]

输出最优路径：

#输出路径：
ans=np.where(best==1)
ans_x=ans[0]
ans_y=ans[1]
x=ans_x[0]
print("最优路径：")
print(x+1,end='')
for i in range(31):
    print('->',ans_y[x]+1,end='')
    x=ans_y[x]   

结果：

最优路径：
1-> 15-> 14-> 12-> 13-> 7-> 10-> 9-> 8-> 2-> 4-> 16-> 5-> 6-> 11-> 23-> 19-> 17-> 3-> 18-> 22-> 21-> 20-> 24-> 25-> 26-> 28-> 27-> 30-> 31-> 29-> 1

与LKH算法得到的结果完全一致，参见：https://blog.csdn.net/baidu/article/details/124723962