使用python实现随机正态分布数据，并导出到表格（超详细）

---

一、前言

最近需要大量的正态分布的数据，为了方便，使用python实现随机正态分布，画出理想正态分布图和实际的矩形分布，并导出到表格里面。

二、使用步骤

1.引入库

下面是编写代码所用到的库

import numpy as np   #随机数
import matplotlib.pyplot as plt   #画图
import xlwt    #导出表格

2.随机正态分布生成算法

生成的数据是100*100，且使用了两种生成正态分布的算法。

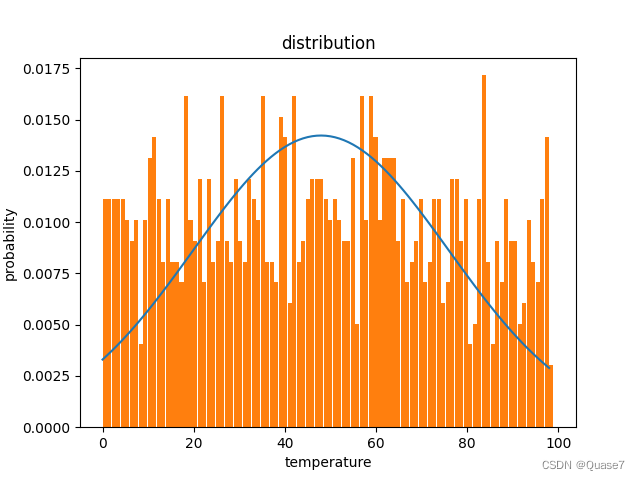
• 一种是基于最大值、最小值范围得到的随机分布。

result = np.random.randint(0, 100, size=100) # 最小值,最大值,数量

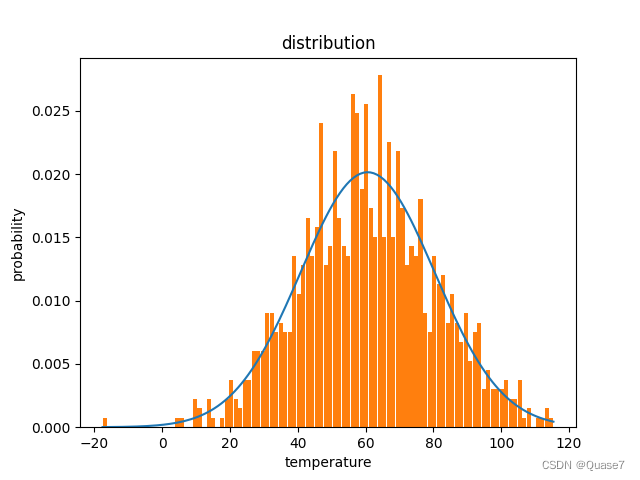
• 一种是基于均值和标准差得到的随机分布。

result = np.random.normal(60, 20, (row,cols))  # 均值,标准差,数量

可以看到，两种算法当中，基于均值和标准差得到的数据更接近正态分布，接下来以第二种做演示。

2.1.利用np.random.normal函数生成二维数据

# 根据均值、标准差,求指定范围的正态分布概率值
def normfun(x, mu, sigma):
  pdf = np.exp(-((x - mu)**2)/(2*sigma**2)) / (sigma * np.sqrt(2*np.pi))
  return pdf

row = 100  #行
cols = 100  #列

#随机生成，整体正态分布
# result = np.random.randint(0, 100, size=100) # 最小值,最大值,数量
result = np.random.normal(60, 20, (row,cols))  # 均值,标准差,数量
#print(result)

生成的数据

2.2.利用for循环生成100*100数据

# 根据均值、标准差,求指定范围的正态分布概率值
def normfun(x, mu, sigma):
  pdf = np.exp(-((x - mu)**2)/(2*sigma**2)) / (sigma * np.sqrt(2*np.pi))
  return pdf

row = 100  #行
cols = 84  #列
result_arr = [[0 for i in range(cols)] for j in range(row)]

#随机生成，行正态分布
for i in range(0,row):
    # result = np.random.randint(0, 100, size=100) # 最小值,最大值,数量
    result = np.random.normal(100, 50, cols)  # 均值,标准差,数量
    x = 0
    for j in result:
        result_arr[i][x] = round(j)   #取整
        x = x+1

for i in range(0,row):
    print(result_arr[i])

对数据做了取整，生成的部分数据

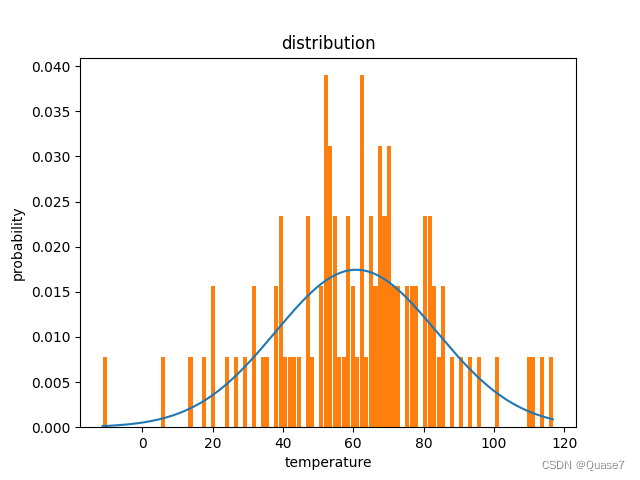
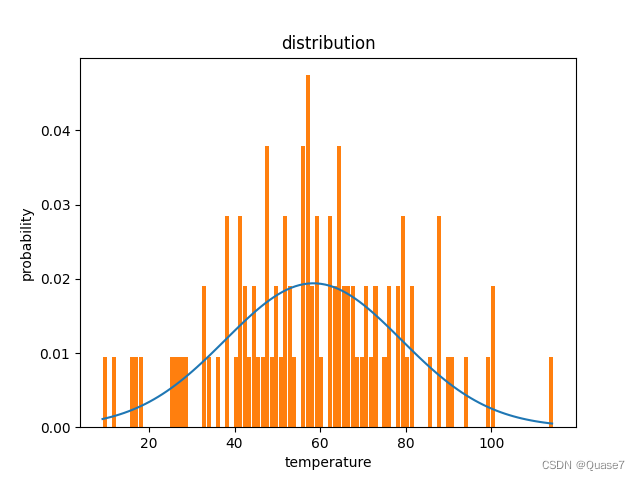
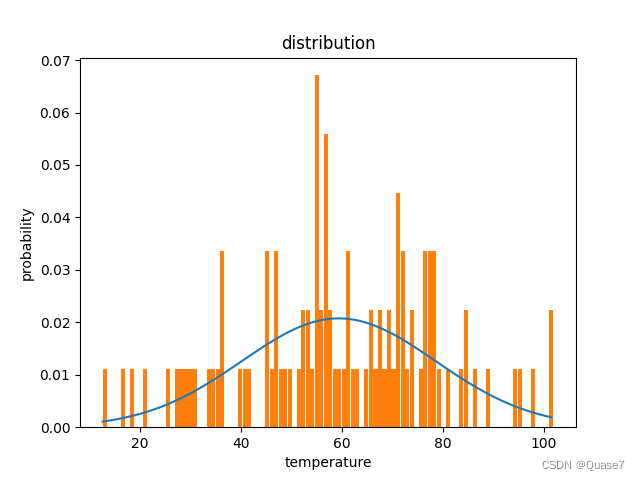
3.生成分布图

可以修改bins个数

#正态分布图
x = np.arange(min(result), max(result), 1)  #步长为1
# 设定 y 轴，载入刚才的正态分布函数
print("均值：",result.mean(), "标准差：",result.std())  #均值、标准差
y = normfun(x, result.mean(), result.std())
plt.plot(x, y) # 这里画出理论的正态分布概率曲线

# 这里画出实际的参数概率与取值关系
plt.hist(result, bins=100, rwidth=0.9, density=True) # bins个柱状图,宽度是rwidth(0~1),=1没有缝隙
plt.title('distribution')
plt.xlabel('temperature')
plt.ylabel('probability')
# 输出
plt.show() # 最后图片的概率和不为1是因为正态分布是从负无穷到正无穷,这里指截取了数据最小值到最大值的分布

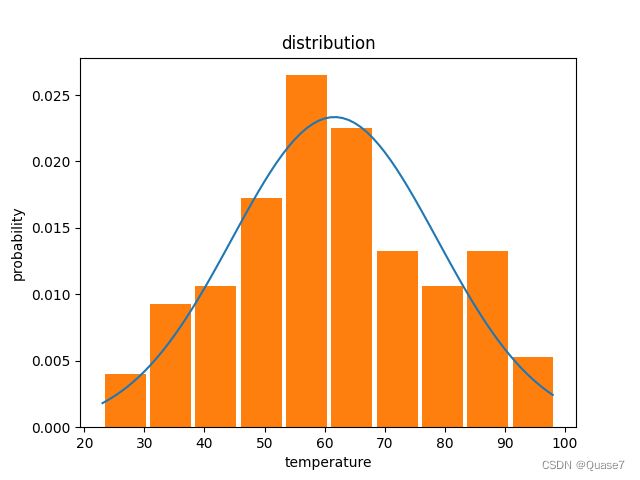
• 可以修改柱状图个数，个数=100，bins=10生成的图示：

• 个数=100，bins=100生成的图示：
  

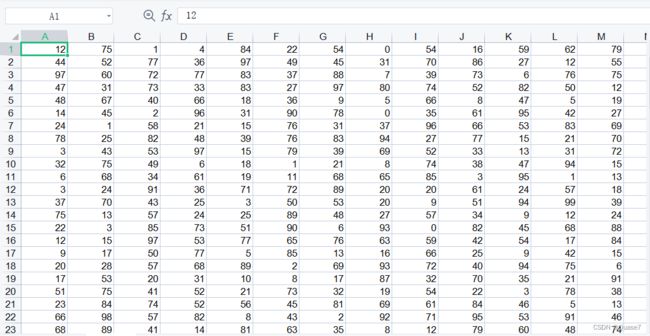
4. 导出到表格

不同的算法对应不同的导出格式

#导出为表格
workbook = xlwt.Workbook(encoding="utf-8")  # 创建workbook对象
worksheet = workbook.add_sheet('sheet1')  # 创建工作表
for i in range(0,row):
    for j in range(0,cols):
        worksheet.write(i, j, result_arr[i][j])
workbook.save('test.xls')

生成的部分数据

5. 完整算法

虽然采取了不同的算法，但总体思路是一样的，但是会有一些细节上的改动，下面将利用函数自身生成的数据算法与利用for循环算法生成的数据结果一并展示。

5.1.利用np.random.normal函数生成二维数据

import numpy as np
import matplotlib.pyplot as plt
import xlwt

# 根据均值、标准差,求指定范围的正态分布概率值
def normfun(x, mu, sigma):
  pdf = np.exp(-((x - mu)**2)/(2*sigma**2)) / (sigma * np.sqrt(2*np.pi))
  return pdf

row = 100  #行
cols = 100  #列

#随机生成，整体正态分布
#result = np.random.randint(0, 100, size=1000) # 最小值,最大值,数量
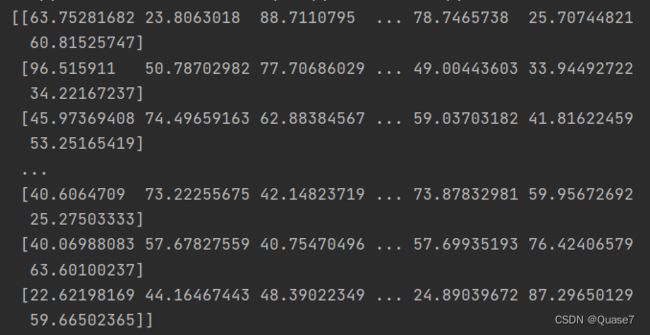
result = np.random.normal(60, 20, (row,cols))  # 均值,标准差,数量
print(result)

#导出为表格

n=0
workbook = xlwt.Workbook(encoding="utf-8")  # 创建workbook对象
worksheet = workbook.add_sheet('sheet1')  # 创建工作表
for i in range(0,row):
    for j in range(0,cols):
        worksheet.write(i, j, round(result[i][j]))
workbook.save('test_3.xls')

#正态分布图
result = result[2]
x = np.arange(min(result), max(result), 1)  #步长为1
# 设定 y 轴，载入刚才的正态分布函数
print("均值：",result.mean(), "标准差：",result.std())  #均值、标准差
y = normfun(x, result.mean(), result.std())
plt.plot(x, y) # 这里画出理论的正态分布概率曲线

# 这里画出实际的参数概率与取值关系
plt.hist(result, bins=100, rwidth=0.9, density=True) # bins个柱状图,宽度是rwidth(0~1),=1没有缝隙
plt.title('distribution')
plt.xlabel('temperature')
plt.ylabel('probability')
# 输出
plt.show() # 最后图片的概率和不为1是因为正态分布是从负无穷到正无穷,这里指截取了数据最小值到最大值的分布

5.2.利用for循环生成100*100数据

import numpy as np
import matplotlib.pyplot as plt
import xlwt

# 根据均值、标准差,求指定范围的正态分布概率值
def normfun(x, mu, sigma):
  pdf = np.exp(-((x - mu)**2)/(2*sigma**2)) / (sigma * np.sqrt(2*np.pi))
  return pdf

row = 100  #行
cols = 100  #列
result_arr = [[0 for i in range(cols)] for j in range(row)]

#随机生成，行正态分布
for i in range(0,row):
    # result = np.random.randint(0, 100, size=100) # 最小值,最大值,数量
    result = np.random.normal(60, 20, cols)  # 均值,标准差,数量
    #print(result)
    x = 0
    for j in result:
        result_arr[i][x] = round(j)
        x = x+1

for i in range(0,row):
    print(result_arr[i])

#导出为表格
workbook = xlwt.Workbook(encoding="utf-8")  # 创建workbook对象
worksheet = workbook.add_sheet('sheet1')  # 创建工作表
for i in range(0,row):
    for j in range(0,cols):
        worksheet.write(i, j, result_arr[i][j])
workbook.save('test_2.xls')


x = np.arange(min(result), max(result), 1)  #步长为1
# 设定 y 轴，载入刚才的正态分布函数
print(result.mean(), result.std())  #均值、标准差
y = normfun(x, result.mean(), result.std())
plt.plot(x, y) # 这里画出理论的正态分布概率曲线

# 这里画出实际的参数概率与取值关系
plt.hist(result, bins=100, rwidth=0.9, density=True) # bins个柱状图,宽度是rwidth(0~1),=1没有缝隙
plt.title('distribution')
plt.xlabel('temperature')
plt.ylabel('probability')
# 输出
plt.show() # 最后图片的概率和不为1是因为正态分布是从负无穷到正无穷,这里指截取了数据最小值到最大值的分布

总结

以上就是今天要讲的内容，本文仅仅简单介绍了使用python随机生成正态分布的数据，画图，并导出。正态分布是机器学习中很常见的一种需求，往往需要大量的数据进行测试，此时，本文的方法就可以大大减少因数据而花费的时间啦！
如有问题，欢迎评论区留言啊！