SSIM结构相似性算法

应用场景

结构相似性，是一种衡量两幅图像相似度的指标，通常用作图像质量评估，在图像重建、压缩领域，可以计算输出图像与原图的差距。

MSE

有很多算法可以计算输出图像与原图的差距，其中最常用的一种是 Mean Square Error loss（MSE）。它的计算公式很简单：

$MSE=\frac{1}{n}\sum [I_i-K_i{]}^2$

就是计算重建图像与输入图像的像素差的平方，然后在全图上求平均。
有时候两张图片只是亮度不同，但是之间的 MSE loss 相差很大。而一幅很模糊与另一幅很清晰的图，它们的 MSE loss 可能反而相差很小:

结合神经科学的研究，认为我们人类衡量两幅图的距离时，更偏重于两图的结构相似性，而不是逐像素计算两图的差异。

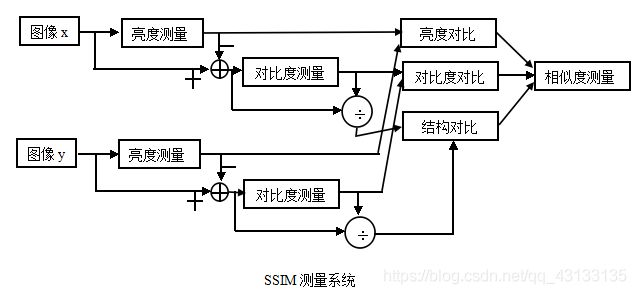
SSIM算法

SSIM使用的两张图像中，一张为未经压缩的无失真图像，另一张为失真后的图像。

相似性按三个维度进行比较：

1. 亮度（luminance）l(x,y)
2. 对比度（contrast）c(x,y)
3. 结构（structure）s(x,y)

最终相似度为这三者的函数：

亮度

以平均灰度来作为亮度测量的估计：

对比度

所谓对比度，就是图像明暗的变化剧烈程度，也就是像素值的标准差，测量系统知道要把平均灰度值从信号中去除，对于离散信号，可使用标准差来做对比度估量值。

结构

需要注意的是，对一幅图而言，其亮度和对比度都是标量，而其结构显然无法用一个标量表示，而是应该用该图所有像素组成的向量来表示。同时，研究结构相似度时，应该排除亮度和对比度的影响，即排除均值和标准差的影响，可用归一化图像向量$(x-{\mu }_x)$来做结构对比估计。该向量长度为

${\sum }_{i=1}^N(x_i-{\mu }_x{)}^2=\sqrt{N-1}\ast {\sigma }_x$

相似函数

三个公式定量计算这三者的相似性，公式的设计遵循三个原则：

1. 对称性：$S(x,y)=S(y,x)$
2. 有界性：$S(x,y)\le 1$
3. 极限值唯一：$S(x,y)=1$当且仅当 $x=y$

作者用如下公式衡量两幅图 x 和 y 的亮度相似度：

$l(x,y)=\frac{2{\mu }_x{\mu }_y+C1}{{\mu }_x^2+{\mu }_y^2+C_1}$

这里$C_1$ 是为了防止分母为零的情况，且：

$C_1={\left(K_{1}L\right)}^2$

其中$K_1\ll 1$是一个常数，具体代码中的取值为 0.01，L 是灰度的动态范围，由图像的数据类型决定，如果数据为 uint8 型，则 L=255。该公式对称且小于等于1，当 x = y 时等号成立。

对比度的相似度（标准差）公式和亮度（均值）公式极为相似，，所以相似度也可以借鉴过来，作者定义对比度相似度：
不过把均值换成了方差，作者定义：

$c(\mathrm{x},\mathrm{y})=\frac{2{\sigma }_{\mathrm{x}}{\sigma }_{\mathrm{y}}+C_2}{{\sigma }_{\mathrm{x}}^2+{\sigma }_{\mathrm{y}}^2+C_2}$
其中：

$C_2={\left(K_{2}L\right)}^2$

一般$K_2$在代码中取 0.03。该公式也对称且小于等于1，当 x = y 时等号成立。

对于结构相似度，可以采用是归一化的两个向量：$\frac{\mathrm{x}-{\mu }_x}{\sqrt{N-1}\ast {\sigma }_x}$和$\frac{\mathrm{y}-{\mu }_y}{\sqrt{N-1}\ast {\sigma }_y}$之间的关系来衡量。
它们的余弦相似度为：

$\begin{array}{r}s(\mathrm{x},\mathrm{y})=\left(\frac{1}{\sqrt{N-1}}\frac{\mathrm{x}-{\mu }_{\mathrm{x}}}{{\sigma }_{\mathrm{x}}}\right)\cdot \left(\frac{1}{\sqrt{N-1}}\frac{\mathrm{y}-{\mu }_{\mathrm{y}}}{{\sigma }_{\mathrm{y}}}\right)\\ =\frac{1}{{\sigma }_{\mathrm{x}}{\sigma }_{\mathrm{y}}}\left(\frac{1}{N-1}\sum _{i=1}^N\left(x_i-{\mu }_{\mathrm{x}}\right)\left(y_i-{\mu }_{\mathrm{y}}\right)\right)\end{array}$
​
上式中第二行括号内的部分为协方差公式：

${\sigma }_{\mathrm{x}\mathrm{y}}=\frac{1}{N-1}{\sum }_{i=1}^N\left(x_i-{\mu }_{\mathrm{x}}\right)\left(y_i-{\mu }_{\mathrm{y}}\right)$
为了防止分母为0，分子分母同时加$C_3$：

$s(\mathrm{x},\mathrm{y})=\frac{{\sigma }_{\mathrm{x}\mathrm{y}}+C_3}{{\sigma }_{\mathrm{x}}{\sigma }_{\mathrm{y}}+C_3}$

SSIM

根据上面三个公式，定义两幅图像的相似度为：
$SSIM(x,y)=l(x,y)\cdot c(x,y)\cdot s(x,y)$

可以巧妙的令$C_3=C_2/2$，使得$c(\mathrm{x},\mathrm{y})$的分子和 $s(\mathrm{x},\mathrm{y})$ 的分母可以约分，最终得到 SSIM 的公式：

$\mathrm{SSIM}(\mathrm{x},\mathrm{y})=\frac{\left(2{\mu }_{\mathrm{x}}{\mu }_{\mathrm{y}}+C_1\right)\left(2{\sigma }_{\mathrm{x}\mathrm{y}}+C_2\right)}{\left({\mu }_{\mathrm{x}}^2+{\mu }_{\mathrm{y}}^2+C_1\right)\left({\sigma }_{\mathrm{x}}^2+{\sigma }_{\mathrm{y}}^2+C_2\right)}$

MSSIM

上面的 SSIM 不能用于一整幅图，因为在整幅图的跨度上，均值和方差往往变化剧烈；同时，图像上不同区块的失真程度也有可能不同，不能一概而论；此外类比人眼睛每次只能聚焦于一处的特点，采用 sliding window 以步长为 1 计算两幅图各个对应 sliding window 下的 patch 的 SSIM，然后取平均值作为两幅图整体的 SSIM，称为 Mean SSIM。简写为 MSSIM（注意和后续出现的 multi-scale SSIM：MS-SSIM 作区分）。

假如整幅图有 M 个 patch，那么 MSSIM 公式为：

$\mathrm{MSSIM}(\mathrm{X},\mathrm{Y})=\frac{1}{M}{\sum }_{j=1}^M\mathrm{SSIM}\left({\mathrm{x}}_j,{\mathrm{y}}_j\right)$

优化技巧

需要知道的数学公式大概是：

${\sigma }_{\mathrm{x}}^2=E\left[{\mathrm{x}}^2\right]-E^2[\mathrm{x}]$

${\sigma }_{\mathrm{x}\mathrm{y}}^2=E[\mathrm{x}\mathrm{y}]-E[\mathrm{x}]E[\mathrm{y}]$