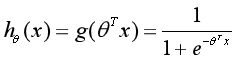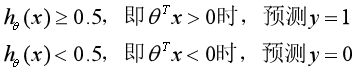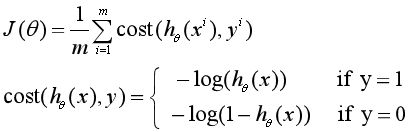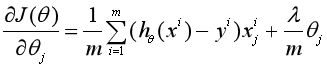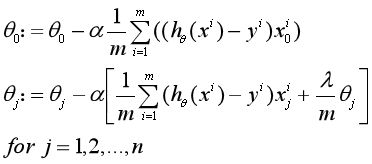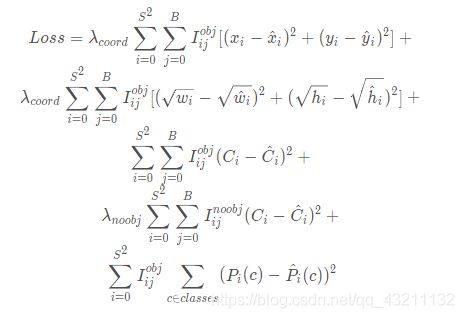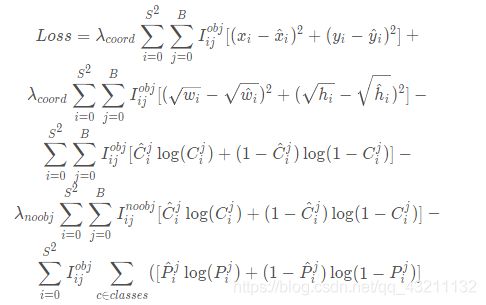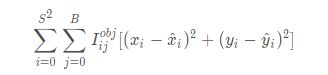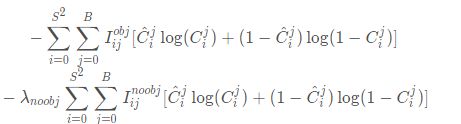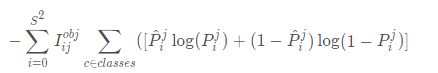logistic回归分类与softmax回归
目录
Logistic回归
逻辑回归的定义式：
损失函数
梯度下降
Logistic回归防止过拟合：
Softmax回归：
loss函数
逻辑回归与Softmax回归的联系
与神经网络的关系
logistic回归（多分类）和softmax的关系：
YOLOV3中的逻辑分类应用
Logistic回归
Logistic回归（LR）：是一种常用的处理二分类问题的模型。
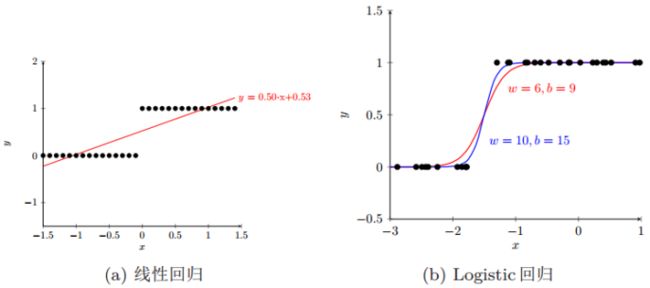
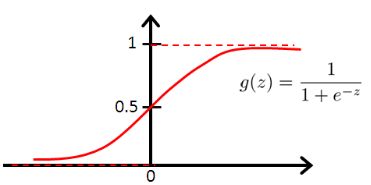
二分类问题中，把结果y分成两个类，正类和负类。因变量y∈{0, 1}，0是负类，1是正类。线性回归
的输出值在负无穷到正无穷的范围上，并不好区分是正类还是负类。因此引入非线性变换，把线性回归的输出值压缩到（0, 1）之间，那就成了Logistic回归
，使得
≥0.5时，预测y=1，而当
<0.5时，预测y=0。
逻辑回归的定义式：
，x代表样本的特征向量。
其中，
为sigmoid函数，
可以理解为预测为正类的概率，即后验概率
，
的取值范围是(0, 1)。。
所以Logistic回归模型就是：
判断类别：
对loss函数求导得到：
当类别y=1时，损失随着
的减小而增大，
为1时，损失为0；
当类别y=0时，损失随着的增大而增大，
为0时，损失为0。
损失函数
这个损失函数叫做对数似然损失函数，也叫：交叉熵损失函数（cross entropy loss）。这个损失函数是个凸函数，因此可以用梯度下降法求得使损失函数最小的参数。
梯度下降
Logistic回归防止过拟合：
在损失函数中加入参数θj的L2范数，限制θj的大小，以解决过拟合问题，那么加入正则化项的损失函数为：
相应的，此时的梯度下降算法为：
重复以下步骤直至收敛：
Softmax回归：
Softmax回归处理多分类问题，假设函数
形式如下：
和逻辑回归一样，得到：
loss函数
其中的1{.}是一个指示性函数，即当大括号中的值为真时，该函数的结果就为1，否则其结果就为0。
然后计算损失函数的偏导函数，得到：
之后就可以用如果要用梯度下降法，或者L-BFGS法求得未知参数。
看上面的推到我们可以发现，对每一个参数减去一个参数，最后的结果没有影响。其实softmax 回归中对参数的最优化解不只一个，每当求得一个优化参数时，如果将这个参数的每一项都减掉同一个数，其得到的损失函数值也是一样的，这说明解不是唯一的。
之所以会出现这样的现象，因为损失函数不是严格非凸的，也就是说在局部最小值点附近是一个”平坦”的，所以在这个参数附近的值都是一样的了。
为避免出现这样的情况，加入正则项（比如说，用牛顿法求解时，hession矩阵如果没有加入规则项，就有可能不是可逆的从而导致了刚才的情况，如果加入了规则项后该hession矩阵就不会不可逆了），加入正则项后的loss函数表达式为：
加入正则项后的loss函数
此时loss函数的偏导函数为：
同样的，我们在逻辑回归中，也可以加上正则项。
逻辑回归与Softmax回归的联系
softmax 回归是逻辑回归的一般形式，两者之间的联系：当类别数k = 2 时，softmax 回归退化为逻辑回归，softmax 回归的假设函数为：
利用softmax回归参数冗余的特点，我们令
，并且从两个参数向量中都减去向量
，得到:
因此，用
来表示
，我们就会发现 softmax 回归器预测其中一个类别的概率为
，另一个类别概率的为
，这与逻辑回归是一致的。
与神经网络的关系
神经网络是一个多层次的分类模型，其实logistic回归和softmax回归可以看出最简单的神经网络，结构如下图所示：
一般的神经网络有输入层，隐含层以及输出层构成，而上图中只有输入层和输出层，而没有隐含层。神经网络处理二分类时，输出层为一个节点，但处理K（K>2）分类问题时，数据节点为K个，这个logistic回归和softmax回归保持一致。值得注意的，在神经网络中的最后一层隐含层和输出层就可以看成是logistic回归或softmax回归模型，之前的层只是从原始输入数据从学习特征，然后把学习得到的特征交给logistic回归或softmax回归处理。
因此，可以把处理分类问题的神经网络分成两部分，特征学习和logistic回归或softmax回归。
logistic回归（多分类）和softmax的关系：
我们已经知道，普通的logistic回归只能针对二分类(Binary Classification)问题，要想实现多个类别的分类，我们必须要改进logistic回归，让其适应多分类问题。
关于这种改进，有两种方式可以做到。
第一种方式是直接根据每个类别，都建立一个二分类器，带有这个类别的样本标记为1，带有其他类别的样本标记为0。假如我们有k个类别，最后我们就得到了k个针对不同标记的普通的logistic分类器。
第二种方式是修改logistic回归的损失函数，让其适应多分类问题。这个损失函数不再笼统地只考虑二分类非1就0的损失，而是具体考虑每个样本标记的损失。这种方法叫做softmax回归，即logistic回归的多分类版本。
我们首先简单介绍第一种方式。
对于二分类问题，我们只需要一个分类器即可，但是对于多分类问题，我们需要多个分类器才行。假如给定数据集
，它们的标记
，即这些样本有k个不同的类别。
我们挑选出标记为
的样本，将挑选出来的带有标记c的样本的标记置为1，将剩下的不带有标记c的样本的标记置为0。然后就用这些数据训练出一个分类器，我们得到
（表示针对标记c的logistic分类函数）。
按照上面的步骤，我们可以得到k个不同的分类器。针对一个测试样本，我们需要找到这k个分类函数输出值最大的那一个，即为测试样本的标记：
下面我们介绍softmax回归。
对于有k个标记的分类问题，分类函数是下面这样：
在这里，我们将上式的所有的组合起来，用矩阵
来表示，即：\
这时候，softmax回归算法的代价函数如下所示（其中sign(expression is true)=1):
我们可以把logistic回归的损失函数改为如下形式：
很显然，softmax是logistic的推广，一般化。
但是，需要特别注意的是，对于
,softmax回归和logistic回归的计算方式是不同的（不大明白哪里不同），不管是二分类还是多分类，都是一个主要区别。
对于选择softmax分类器还是k个logistic分类器，取决于所有类别之间是否互斥。所有类别之间明显互斥用softmax分类器，所有类别之间不互斥有交叉的情况下最好用k个logistic分类器。
参考：logistic回归（二分类）和Softmax回归的关系、logistic回归（多分类）和Softmax的关系_hahaha_2017的博客-CSDN博客_softmax 逻辑回归
YOLOV3中的逻辑分类应用
先回顾下YOLOv1的损失函数：
yolov2的损失函数：
只是在yolov1基础上改动了关于bbox的w和h的损失计算方式 即从：
去掉了w和h的二次根号，作者认为没有必要。
YOLOv3的损失函数：
是在yolov2基础上改动的，最大的变动是分类损失换成了二分交叉熵，这是由于yolov3中剔除了softmax改用logistic。
一项一项分析损失函数：
-
中心坐标误差
- 置信度误差
首先需要知道，置信度误差使用交叉熵来表示。另外需要清楚不管anchor box是否负责某个目标，都会计算置信度误差。因为置信度表示：框出的box内确实有物体的自信程度和框出的box将整个物体的所有特征都包括进来的自信程度。具体可以参考博客。
损失函数分为两部分：有物体，没有物体，其中没有物体损失部分还增加了权重系数。添加权重系数的原因是，对于一幅图像，一般而言大部分内容是不包含待检测物体的，这样会导致没有物体的计算部分贡献会大于有物体的计算部分，这会导致网络倾向于预测单元格不含有物体。因此，我们要减少没有物体计算部分的贡献权重，比如取值为：0.5。
第一项是：存在对象的bounding box的置信度误差。带有
意味着只有"负责"（IOU比较大）预测的那个bounding box的置信度才会计入误差。
第二项是：不存在对象的bounding box的置信度误差。因为不存在对象的bounding box应该老老实实的说"我这里没有对象"，也就是输出尽量低的置信度。如果它不恰当的输出较高的置信度，会与真正"负责"该对象预测的那个bounding box产生混淆。其实就像对象分类一样，正确的对象概率最好是1，所有其它对象的概率最好是0。
- 分类误差
首先需要知道分类误差也是选择了交叉熵作为损失函数。当第i个网格的第j个anchor box负责某一个真实目标时，那么这个anchor box所产生的bounding box才会去计算分类损失函数。
参考：【论文理解】yolov3损失函数_DLUT_yan的博客-CSDN博客_yolov3损失函数