教你几招搞定 LSTMS 的独门绝技—理解与代码校正
雷锋网翻译了一篇技术博客(标题:Taming LSTMs: Variable-sized mini-batches and why PyTorch is good for your health,作者:William Falcon, 翻译 | 赵朋飞 马力群 涂世文 整理 | MY),该博客主要讲述了pytorch下输入为变长序列的LSTM的处理方式,文中所举案例简单,描述详尽,语言通俗易懂,可作为变长序列处理的最好的入门案例。然而,不知何故,代码中存在很多错误,使得其作为入门教材的效果大打折扣。另一方面,该博客没有输出一些关键方法的结果,加大了初学者的理解难度。因此,本文以翻译稿为主要蓝本,结合自己的理解,给出本人改正后的代码及关键中间结果,以期能够更好地理解和处理变长序列。
如果你用过 PyTorch 进行深度学习研究和实验的话,你可能经历过欣喜愉悦、能量爆棚的体验,甚至有点像是走在阳光下,感觉生活竟然如此美好 。但是直到你试着用 PyTorch 实现可变大小的 mini-batch RNNs 的时候,瞬间一切又回到了解放前。
不怕,我们还是有希望的。读完这篇文章,你又会找回那种感觉,你和 PyTorch步入阳光中,此时你的循环神经网络模型的准确率又创新高,而这种准确率你只在 Arxiv 上读到过。真让人觉得兴奋!
我们将告诉你几个独门绝技:
1.如何在PyTorch中采用 mini-batch 中的可变大小序列实现 LSTM 。
2. PyTorch中pack_padded_sequence 和 pad_packed_sequence 的原理和作用。
3.在基于时间维度的反向传播算法中屏蔽(Mask Out)用于填充的符号。
Tips: 文本填充,使所有文本长度相等;pack_padded_sequence , 运行LSTM;使用pad_packed_sequence;扁平化所有输出和标签, 屏蔽填充输出, 计算交叉熵损失函数(Cross-Entropy)。
为何知其难而为之?
当然是速度和性能啦。
将可变长度元素同时输入到 LSTM 曾经可是一个艰巨的技术挑战,不过像 PyTorch 这样的框架已经基本解决了( Tensorflow 也有一个很好的解决方案,但它看起来非常非常复杂)。
此外,文档也没有很清楚的解释,用例也很老旧。正确的做法是使用来自多个示样本的梯度,而不是仅仅来自一个样本。这将加快训练速度,提高梯度下降的准确性 。
尽管 RNNs 很难并行化,因为每一步都依赖于上一步,但是使用 mini-batch 在速度上将会使其得到很大的提升。
序列标注
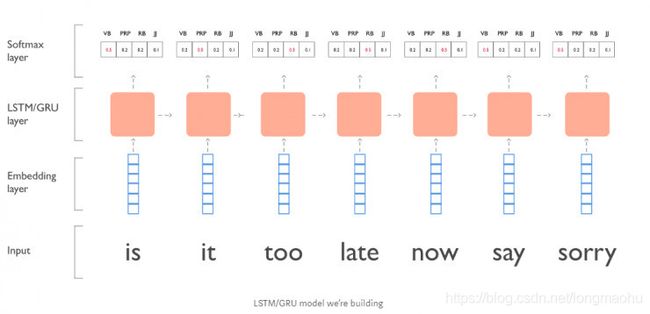
先来尝试一个简单的序列标注问题,在这里我们会创建一个 LSTM/GRU 模型 对贾斯汀·比伯的歌词做词性标注。譬如:“is it too late now to say sorry?” (移除 ’to’ 和 ’?’ )。
数据格式化
在实际情况中你会做大量的格式化处理,但在这里由于篇幅限制我们不会这样做。为简单起见,让我们用不同长度的序列来制作这组人造数据。
sent_1_x = ['is', 'it', 'too', 'late', 'now', 'say', 'sorry']
sent_1_y = ['VB', 'PRP', 'RB', 'RB', 'RB', 'VB', 'JJ']
sent_2_x = ['ooh', 'ooh']
sent_2_y = ['NNP', 'NNP']
sent_3_x = ['sorry', 'yeah']
sent_3_y = ['JJ', 'NNP']
X = [sent_1_x, sent_2_x, sent_3_x]
Y = [sent_1_y, sent_2_y, sent_3_y]
当我们将每个句子输入到嵌入层(Embedding Layer)的时候,每个单词(word)将会映射(mapping)到一个索引(index),所以我们需要将他们转换成整数列表(list)。
这里我们将这些句子映射到相应的词汇表(V)索引。
# map sentences to vocab
vocab = {'': 0, 'is': 1, 'it': 2, 'too': 3, 'late': 4, 'now': 5, 'say': 6, 'sorry': 7, 'ooh': 8, 'yeah': 9}
# fancy nested list comprehension
X = [[vocab[word] for word in sentence] for sentence in X]
print(X)
[[1, 2, 3, 4, 5, 6, 7], [8, 8], [7, 9]]对于分类标签也是一样的(在我们的例子中是 POS 标记),这些不会嵌入 。
tags = {'': 0, 'VB': 1, 'PRP': 2, 'RB': 3, 'JJ': 4, 'NNP': 5}
# fancy nested list comprehension
Y = [[tags[tag] for tag in sentence] for sentence in Y]
print(Y)
[[1, 2, 3, 3, 3, 1, 4], [5, 5], [4, 5]]技巧1:利用填充(Padding)使 mini-batch 中中所有的序列具有相同的长度。
在模型里有着不同长度的是什么?当然不会是我们的每批数据!
利用 PyTorch 处理时,在填充之前,我们需要保存每个序列的长度。我们需要利用这些信息去掩盖(mask out)损失函数,使其不对填充元素进行计算。
import numpy as np
# get the length of each sentence
X_lengths = [len(sentence) for sentence in X]
# create an empty matrix with padding tokens
pad_token = vocab['']
longest_sent = max(X_lengths)
batch_size = len(X)
padded_X = np.ones((batch_size, longest_sent)) * pad_token
# copy over the actual sequences
for i, x_len in enumerate(X_lengths):
sequence = X[i]
padded_X[i, 0:x_len] = sequence[:x_len]
print(padded_X)
[[1. 2. 3. 4. 5. 6. 7.]
[8. 8. 0. 0. 0. 0. 0.]
[7. 9. 0. 0. 0. 0. 0.]]
我们用同样的方法处理标签 :
Y_lengths = [len(sentence) for sentence in Y]
# create an empty matrix with padding tokens
pad_token = tags['']
longest_sent = max(Y_lengths)
batch_size = len(Y)
padded_Y = np.ones((batch_size, longest_sent)) * pad_token
# copy over the actual sequences
for i, y_len in enumerate(Y_lengths):
sequence = Y[i]
padded_Y[i, 0:y_len] = sequence[:y_len]
print(padded_Y)
[[1. 2. 3. 3. 3. 1. 4.]
[5. 5. 0. 0. 0. 0. 0.]
[4. 5. 0. 0. 0. 0. 0.]]
数据处理总结:
我们将这些元素转换成索引序列并通过加入 0 元素对每个序列进行填充(Zero Padding),这样每批数据就可以拥有相同的长度。
构建模型
借助 PyTorch 我们可以搭建一个非常简单的 LSTM 网络。模型的层结构如下:
1. 词嵌入层(Embedding Layer)
2. LSTM 层
3. 线性全连接层
4. Softmax 层
import torch
import torch.nn as nn
import torch.nn.functional as F
nb_tags = len(tags) - 1
nb_vocab_words = len(vocab)
batch_size, seq_len=padded_X.shape
embedding_dim=3
nb_lstm_units=10
nb_layers=2
padding_idx = vocab['']
word_embedding = nn.Embedding(
num_embeddings=nb_vocab_words,
embedding_dim=embedding_dim,
padding_idx=padding_idx
)
# design LSTM
lstm = nn.LSTM(
input_size=embedding_dim,
hidden_size=nb_lstm_units,
num_layers=nb_layers,
batch_first=True
)
# output layer which projects back to tag space
hidden_to_tag = nn.Linear(nb_lstm_units, nb_tags)
hidden_a = torch.randn(nb_layers, batch_size, nb_lstm_units).float()
hidden_b = torch.randn(nb_layers, batch_size, nb_lstm_units).float()
技巧2:使用 PyTorch 中的 pack_padded_sequence 和 pad_packed_sequence API
再次重申一下,现在我们输入的一批数据中的每组数据均已被填充为相同长度。
在前向传播中,我们将:
1. 对序列进行词嵌入(Word Embedding)操作
2. 使用 pack_padded_sequence 来确保 LSTM 模型不会处理用于填充的元素。
3. 在 LSTM 上运行 packed_batch
4. 使用 pad_packed_sequence 解包(unpack)pack_padded_sequence 操作后的序列
5. 对 LSTM 的输出进行变换,从而可以被输入到线性全连接层中
6. 再通过对序列计算 log_softmax
7. 最后将数据维度转换回来,最终的数据维度为 (batch_size, seq_len, nb_tags)
# 1. embed the input
# Dim transformation: (batch_size, seq_len) -> (batch_size, seq_len, embedding_dim)
X = torch.tensor(padded_X).long()
X = word_embedding(X)
print('embedded', X)
embedded tensor([[[ 1.3190, 0.0872, -0.2742],
[-0.1677, 1.1510, 0.4656],
[-0.8435, -0.5562, 0.9256],
[-0.8396, -0.0076, -1.5482],
[-0.5656, -1.3909, -0.7842],
[-0.5416, 1.7457, 0.4726],
[ 1.1060, 0.8440, -0.5556]],
[[ 0.6334, -1.5088, 1.0840],
[ 0.6334, -1.5088, 1.0840],
[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000]],
[[ 1.1060, 0.8440, -0.5556],
[ 1.2046, -1.6742, 0.6964],
[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000]]], grad_fn=)
将填充好的tensor根据所输入地参数压缩成实际地数据,同时数据格式变为PackedSequence。它有三个主要的参数, 分别是input, lengths, batch_first. 其中input就是我们填充过的数据, 而lengths就是数据的实际长度, batch_first就简单了, 就是把数据的batch_first放到最前面。
Tips:但是为啥我们需要使用pack_padded_sequence呢? 直接把填充好的数据输入到RNN中不可以吗?实际上是当然可以的, 但是在实际情况中, 数据是这样输入的, 下面给出一个batch的例子。
tensor([[1, 2, 3, 4, 5, 6, 7],
[2, 3, 4, 5, 6, 7, 0]])
输入到RNN的实际上是按照这样的顺序[1, 2], [2, 3], [3, 4], [4, 5], [5, 6], [6, 7], [7, 0]依次输入到RNN中的. 但是我们发现最后一个是[7, 0], 这里的0输入到RNN中, 实际上并没有输出有用的数据, 这样的话就会浪费算力资源, 所以我们使用pack_padded_sequence进行压缩一下。
# Dim transformation: (batch_size, seq_len, embedding_dim) -> (batch_size, seq_len, nb_lstm_units)
# pack_padded_sequence so that padded items in the sequence won't be shown to the LSTM
X = torch.nn.utils.rnn.pack_padded_sequence(X, X_lengths, batch_first=True)
print('pack_padded',X)
pack_padded: PackedSequence(data=tensor([[ 1.3190, 0.0872, -0.2742],
[ 0.6334, -1.5088, 1.0840],
[ 1.1060, 0.8440, -0.5556],
[-0.1677, 1.1510, 0.4656],
[ 0.6334, -1.5088, 1.0840],
[ 1.2046, -1.6742, 0.6964],
[-0.8435, -0.5562, 0.9256],
[-0.8396, -0.0076, -1.5482],
[-0.5656, -1.3909, -0.7842],
[-0.5416, 1.7457, 0.4726],
[ 1.1060, 0.8440, -0.5556]], grad_fn=), batch_sizes=tensor([3, 3, 1, 1, 1, 1, 1]), sorted_indices=None, unsorted_indices=None)
现在,运行LSTM。
X, hidden = lstm(X, (hidden_a, hidden_b))
print('lstm ouput shape in packed seq: ', X[0].size())
print(X)
lstm ouput shape in packed seq: torch.Size([11, 10])
PackedSequence(data=tensor([[ 1.5307e-01, 6.7684e-02, 6.4468e-02, -2.2887e-01, 2.0291e-01,
1.6192e-02, 9.1459e-03, 1.6604e-01, 2.4689e-01, 2.1277e-01],
[-2.0542e-01, -6.3485e-02, 2.1305e-02, -1.8940e-01, 3.6822e-01,
-4.2697e-04, -1.2188e-02, 1.4914e-01, -1.9662e-01, 4.1007e-03],
[-1.8556e-01, 5.8267e-01, -5.5726e-02, 3.2447e-01, -5.6095e-02,
1.0067e-01, 1.5416e-02, -6.1702e-01, -3.9697e-02, 3.5665e-03],
[ 1.1510e-01, -3.5210e-02, 1.6324e-01, -1.1573e-01, 1.2481e-01,
-1.3048e-01, 1.2843e-02, 2.3278e-03, 5.5453e-02, 1.4491e-01],
[-1.8321e-01, -1.2067e-01, 5.8485e-02, -1.5943e-01, 2.3355e-01,
-1.0162e-01, -2.4926e-02, -7.1134e-02, -1.7803e-01, 3.8604e-02],
[-7.5403e-02, 1.5720e-01, 5.6410e-02, 4.4938e-02, -3.5079e-02,
-1.0616e-02, 6.9829e-02, -3.6775e-01, -4.3459e-02, 7.8495e-02],
[ 6.3267e-03, -1.0364e-01, 1.5995e-01, -1.1714e-01, 8.7210e-02,
-1.7794e-01, -6.6597e-03, -9.0191e-02, 3.0669e-03, 1.1943e-01],
[-4.8220e-02, -1.3315e-01, 1.5506e-01, -1.2272e-01, 7.2997e-02,
-1.8515e-01, -3.2535e-02, -1.3140e-01, -2.9254e-02, 1.0733e-01],
[-7.8605e-02, -1.4908e-01, 1.4581e-01, -1.3867e-01, 6.2283e-02,
-1.9139e-01, -5.0125e-02, -1.5407e-01, -4.2093e-02, 9.7522e-02],
[-9.3640e-02, -1.4058e-01, 1.4463e-01, -1.4144e-01, 7.2176e-02,
-1.7028e-01, -4.0201e-02, -1.7073e-01, -6.1939e-02, 1.0614e-01],
[-1.0190e-01, -1.3188e-01, 1.3591e-01, -1.2254e-01, 8.6571e-02,
-1.6958e-01, -4.1146e-02, -1.7248e-01, -8.0702e-02, 9.7578e-02]],
grad_fn=), batch_sizes=tensor([3, 3, 1, 1, 1, 1, 1]), sorted_indices=None, unsorted_indices=None)
从上面输出的结果中可以看出,由于lstm运行时没有计算pading, lstm的输出是(11,10),而常规的lstm的输出应该是(3,7,10),所以需要把原来的padding加上,还原成(3,7,10)。pad_packed_sequence方法可以完成这个工作。
# undo the packing operation
X, _ = torch.nn.utils.rnn.pad_packed_sequence(X, batch_first=True)
print('un packed:', X.size())
print(X)
un packed: torch.Size([3, 7, 10])
tensor([[[ 1.5307e-01, 6.7684e-02, 6.4468e-02, -2.2887e-01, 2.0291e-01,
1.6192e-02, 9.1459e-03, 1.6604e-01, 2.4689e-01, 2.1277e-01],
[ 1.1510e-01, -3.5210e-02, 1.6324e-01, -1.1573e-01, 1.2481e-01,
-1.3048e-01, 1.2843e-02, 2.3278e-03, 5.5453e-02, 1.4491e-01],
[ 6.3267e-03, -1.0364e-01, 1.5995e-01, -1.1714e-01, 8.7210e-02,
-1.7794e-01, -6.6597e-03, -9.0191e-02, 3.0669e-03, 1.1943e-01],
[-4.8220e-02, -1.3315e-01, 1.5506e-01, -1.2272e-01, 7.2997e-02,
-1.8515e-01, -3.2535e-02, -1.3140e-01, -2.9254e-02, 1.0733e-01],
[-7.8605e-02, -1.4908e-01, 1.4581e-01, -1.3867e-01, 6.2283e-02,
-1.9139e-01, -5.0125e-02, -1.5407e-01, -4.2093e-02, 9.7522e-02],
[-9.3640e-02, -1.4058e-01, 1.4463e-01, -1.4144e-01, 7.2176e-02,
-1.7028e-01, -4.0201e-02, -1.7073e-01, -6.1939e-02, 1.0614e-01],
[-1.0190e-01, -1.3188e-01, 1.3591e-01, -1.2254e-01, 8.6571e-02,
-1.6958e-01, -4.1146e-02, -1.7248e-01, -8.0702e-02, 9.7578e-02]],
[[-2.0542e-01, -6.3485e-02, 2.1305e-02, -1.8940e-01, 3.6822e-01,
-4.2697e-04, -1.2188e-02, 1.4914e-01, -1.9662e-01, 4.1007e-03],
[-1.8321e-01, -1.2067e-01, 5.8485e-02, -1.5943e-01, 2.3355e-01,
-1.0162e-01, -2.4926e-02, -7.1134e-02, -1.7803e-01, 3.8604e-02],
[ 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00,
0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00],
[ 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00,
0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00],
[ 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00,
0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00],
[ 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00,
0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00],
[ 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00,
0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00]],
[[-1.8556e-01, 5.8267e-01, -5.5726e-02, 3.2447e-01, -5.6095e-02,
1.0067e-01, 1.5416e-02, -6.1702e-01, -3.9697e-02, 3.5665e-03],
[-7.5403e-02, 1.5720e-01, 5.6410e-02, 4.4938e-02, -3.5079e-02,
-1.0616e-02, 6.9829e-02, -3.6775e-01, -4.3459e-02, 7.8495e-02],
[ 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00,
0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00],
[ 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00,
0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00],
[ 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00,
0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00],
[ 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00,
0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00],
[ 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00,
0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00]]],
grad_fn=)
运行线性连接层。
# 3. Project to tag space
# Dim transformation: (batch_size, seq_len, nb_lstm_units) -> (batch_size * seq_len, nb_lstm_units)
# this one is a bit tricky as well. First we need to reshape the data so it goes into the linear layer
X = X.contiguous()
X = X.view(-1, X.shape[2])
# run through actual linear layer
X = hidden_to_tag(X)
print(X)
tensor([[-0.2492, -0.0340, 0.2604, -0.1128, 0.1133],
[-0.2084, 0.0336, 0.1851, -0.1483, 0.1951],
[-0.1816, 0.0132, 0.1213, -0.1773, 0.2254],
[-0.1661, 0.0026, 0.0929, -0.1934, 0.2455],
[-0.1564, -0.0099, 0.0747, -0.2039, 0.2592],
[-0.1581, -0.0089, 0.0738, -0.2018, 0.2586],
[-0.1506, -0.0080, 0.0705, -0.1919, 0.2626],
[-0.0720, 0.0107, 0.0915, -0.0448, 0.2584],
[-0.0969, -0.0102, 0.0507, -0.1165, 0.2872],
[-0.1556, 0.0033, 0.1379, -0.1076, 0.1813],
[-0.1556, 0.0033, 0.1379, -0.1076, 0.1813],
[-0.1556, 0.0033, 0.1379, -0.1076, 0.1813],
[-0.1556, 0.0033, 0.1379, -0.1076, 0.1813],
[-0.1556, 0.0033, 0.1379, -0.1076, 0.1813],
[-0.2086, -0.2195, 0.1842, -0.1434, 0.1055],
[-0.2085, -0.0694, 0.1326, -0.1655, 0.1689],
[-0.1556, 0.0033, 0.1379, -0.1076, 0.1813],
[-0.1556, 0.0033, 0.1379, -0.1076, 0.1813],
[-0.1556, 0.0033, 0.1379, -0.1076, 0.1813],
[-0.1556, 0.0033, 0.1379, -0.1076, 0.1813],
[-0.1556, 0.0033, 0.1379, -0.1076, 0.1813]],
grad_fn=)
最后,运行log_softmax函数,以便分类。
Tips:log_softmax函数等价于log(softmax(x)),对应的损失函数为nn.NLLLoss。 nn.NLLLoss的输入是一个对数概率向量和一个目标标签。nn.NLLLoss的结果就是将输出与Label对应的那个值拿出来,再去掉负号,然后求均值。(参考:Pytorch损失函数torch.nn.NLLLoss()详解 https://blog.csdn.net/Jeremy_lf/article/details/102725285)。
# 4. Create softmax activations bc we're doing classification
# Dim transformation: (batch_size * seq_len, nb_lstm_units) -> (batch_size, seq_len, nb_tags)
X = F.log_softmax(X, dim=1)
# I like to reshape for mental sanity so we're back to (batch_size, seq_len, nb_tags)
X = X.view(batch_size, seq_len, nb_tags)
Y_hat = X
print(Y_hat)
tensor([[[-1.8699, -1.6547, -1.3603, -1.7335, -1.5074],
[-1.8429, -1.6009, -1.4494, -1.7828, -1.4395],
[-1.8042, -1.6095, -1.5014, -1.7999, -1.3972],
[-1.7854, -1.6166, -1.5264, -1.8126, -1.3738],
[-1.7727, -1.6262, -1.5416, -1.8202, -1.3571],
[-1.7743, -1.6251, -1.5424, -1.8180, -1.3576],
[-1.7702, -1.6276, -1.5490, -1.8115, -1.3570]],
[[-1.7375, -1.6548, -1.5739, -1.7103, -1.4071],
[-1.7402, -1.6535, -1.5926, -1.7598, -1.3561],
[-1.7856, -1.6267, -1.4921, -1.7376, -1.4487],
[-1.7856, -1.6267, -1.4921, -1.7376, -1.4487],
[-1.7856, -1.6267, -1.4921, -1.7376, -1.4487],
[-1.7856, -1.6267, -1.4921, -1.7376, -1.4487],
[-1.7856, -1.6267, -1.4921, -1.7376, -1.4487]],
[[-1.7761, -1.7870, -1.3833, -1.7109, -1.4620],
[-1.8014, -1.6624, -1.4603, -1.7584, -1.4240],
[-1.7856, -1.6267, -1.4921, -1.7376, -1.4487],
[-1.7856, -1.6267, -1.4921, -1.7376, -1.4487],
[-1.7856, -1.6267, -1.4921, -1.7376, -1.4487],
[-1.7856, -1.6267, -1.4921, -1.7376, -1.4487],
[-1.7856, -1.6267, -1.4921, -1.7376, -1.4487]]],
grad_fn=)
技巧 3 : 屏蔽(Mask Out )我们并不想在损失函数中处理的网络输出
最终,我们准备要计算损失函数了。这里的重点在于我们并不想让用于填充的元素影响到最终的输出。
Tips:最好的方法是将所有的网络输出和标签展平。然后计算其所在序列的损失值。
定义损失函数如下。
def loss(Y_hat, Y, X_lengths):
# before we calculate the negative log likelihood, we need to mask out the activations
# this means we don't want to take into account padded items in the output vector
# simplest way to think about this is to flatten ALL sequences into a REALLY long sequence
# and calculate the loss on that.
# flatten all the labels
Y = Y.view(-1)
# flatten all predictions
Y_hat = Y_hat.view(-1, nb_tags)
# create a mask by filtering out all tokens that ARE NOT the padding token
tag_pad_token = tags['']
mask = (Y > tag_pad_token).float()
print('mask:', mask)
# count how many tokens we have
nb_tokens = int(torch.sum(mask).item()) #torch.sum(mask).data[0]
print('tokens number:', nb_tokens)
# pick the values for the label and zero out the rest with the mask
_,ix = torch.topk(Y_hat,1,dim=1)
print('Y_hat max', ix.view(-1))
Y = Y – 1 # the code is none in original article, added by me.
print('Y',Y)
# calculate curracy
count = 0
for i in range(21):
if (Y.numpy())[i] == (ix.view(-1).numpy())[i]:
count += 1
print('accuracy:', str(count / nb_tokens * 100) + '%')
Y_hat = Y_hat[range(Y_hat.shape[0]), Y] * mask
# compute cross entropy loss which ignores all tokens
ce_loss = -torch.sum(Y_hat) / nb_tokens
return ce_loss
最后,计算损失。
Y = torch.tensor(padded_Y).long()
loss = loss(Y_hat, Y, X_lengths)
print('loss', loss)mask: tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 0., 0., 0., 0., 1., 1., 0., 0., 0., 0., 0.])
tokens number: 11
Y_hat max tensor([2, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 2, 4, 4, 4, 4, 4, 4])
Y tensor([ 0, 1, 2, 2, 2, 0, 3, 4, 4, -1, -1, -1, -1, -1, 3, 4, -1, -1, -1, -1, -1])
accuracy: 27.27272727272727%
loss tensor(1.5931, grad_fn=) 总结一下:
这便是在 PyTorch 中解决 LSTM 变长批输入的最佳实践。
1. 将序列从长到短进行排序
2. 通过序列填充使得输入序列长度保持一致
3. 使用 pack_padded_sequence 确保 LSTM 不会额外处理序列中的填充项(Facebook 的 Pytorch 团队真应该考虑为这个绕口的 API 换个名字 !)
4. 使用 pad_packed_sequence 对步骤 3的操作进行还原
5. 将输出和标记展平为一个长的向量
6. 屏蔽(Mask Out) 你不想要的输出
7. 计算其 Cross-Entropy (交叉熵)
上面给出的是jupyter notebook版本。如果想实现多次训练,可以用.py版本(lstm_pad_pack.py)(https://download.csdn.net/download/longmaohu/12561087)。