机器学习：Python中如何使用最小二乘法

机器学习：Python中如何使用最小二乘法

  之所以说”使用”而不是”实现”，是因为python的相关类库已经帮我们实现了具体算法，而我们只要学会使用就可以了。随着对技术的逐渐掌握及积累，当类库中的算法已经无法满足自身需求的时候，我们也可以尝试通过自己的方式实现各种算法。

  言归正传，什么是”最小二乘法”呢？

  定义：最小二乘法（又称最小平方法）是一种数学优化技术，它通过最小化误差的平方和寻找数据的最佳函数匹配。

  作用：利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

  原则：以”残差平方和最小”确定直线位置(在数理统计中，残差是指实际观察值与估计值之间的差)

  数学公式：



  基本思路：对于一元线性回归模型, 假设从总体中获取了n组观察值（X1，Y1），（X2，Y2）， …，（Xn，Yn），对于平面中的这n个点，可以使用无数条曲线来拟合。而线性回归就是要求样本回归函数尽可能好地拟合这组值，也就是说，这条直线应该尽可能的处于样本数据的中心位置。因此，选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。

  实现代码如下，代码中已经详细的给了注释：

复制代码

最小二乘法

import numpy as np ##科学计算库
import scipy as sp ##在numpy基础上实现的部分算法库
import matplotlib.pyplot as plt ##绘图库
from scipy.optimize import leastsq ##引入最小二乘法算法

”’
设置样本数据，真实数据需要在这里处理
”’

样本数据(Xi,Yi)，需要转换成数组(列表)形式

Xi=np.array([6.19,2.51,7.29,7.01,5.7,2.66,3.98,2.5,9.1,4.2])
Yi=np.array([5.25,2.83,6.41,6.71,5.1,4.23,5.05,1.98,10.5,6.3])

”’
设定拟合函数和偏差函数
函数的形状确定过程：
1.先画样本图像
2.根据样本图像大致形状确定函数形式(直线、抛物线、正弦余弦等)
”’

需要拟合的函数func :指定函数的形状

def func(p,x):
k,b=p
return k*x+b

偏差函数：x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的

def error(p,x,y):
return func(p,x)-y

”’
主要部分：附带部分说明
1.leastsq函数的返回值tuple，第一个元素是求解结果，第二个是求解的代价值(个人理解)
2.官网的原话（第二个值）：Value of the cost function at the solution
3.实例：Para=>(array([ 0.61349535, 1.79409255]), 3)
4.返回值元组中第一个值的数量跟需要求解的参数的数量一致
”’

k,b的初始值，可以任意设定,经过几次试验，发现p0的值会影响cost的值：Para[1]

p0=[1,20]

把error函数中除了p0以外的参数打包到args中(使用要求)

Para=leastsq(error,p0,args=(Xi,Yi))

读取结果

k,b=Para[0]
print(“k=”,k,”b=”,b)
print(“cost：”+str(Para[1]))
print(“求解的拟合直线为:”)
print(“y=”+str(round(k,2))+”x+”+str(round(b,2)))

”’
绘图，看拟合效果.
matplotlib默认不支持中文，label设置中文的话需要另行设置
如果报错，改成英文就可以
”’

画样本点

plt.figure(figsize=(8,6)) ##指定图像比例： 8：6
plt.scatter(Xi,Yi,color=”green”,label=”样本数据”,linewidth=2)

画拟合直线

x=np.linspace(0,12,100) ##在0-15直接画100个连续点
y=k*x+b ##函数式
plt.plot(x,y,color=”red”,label=”拟合直线”,linewidth=2)
plt.legend(loc=’lower right’) #绘制图例
plt.show()

复制代码

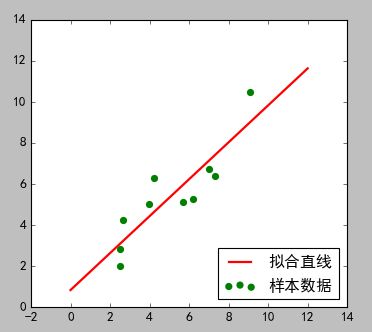
结果如下所示：

输出结果：

  k= 0.900458420439 b= 0.831055638877
  cost：1
  求解的拟合直线为:
  y=0.9x+0.83

绘图结果：

补充说明：简单的列举了直线的情况，曲线的求解方式类似(在另一篇博文中举例了抛物线)，
但是曲线会存在过度拟合的情况，在以后的博客中会讲到。