python中的最小二乘拟合

假设有一组实验数据(x[i], y[i])，我们知道它们之间的函数关系:y = f(x)，通过这些已知信息，需要确定
函数中的一些参数项。例如，如果f是一个线型函数f(x) = k*x+b，那么参数k和b就是我们需要确定的

值。如果将这些参数用p 表示的话，那么我们就是要找到一组p 值使得如下公式中的S函数最小：

这种算法被称之为最小二乘拟合(Least-square fitting)。
scipy中的子函数库optimize已经提供了实现最小二乘拟合算法的函数leastsq。下面是用leastsq进行

数据拟合的一个例子：

# -*- coding: utf-8 -*-
import numpy as np
from scipy.optimize import leastsq
import matplotlib.pyplot as plt

def func(x, p):
    """
    数据拟合所用的函数: A*sin(2*pi*k*x + theta)
    """
    A, k, theta = p#给A,k,theta赋值,其中x作为输入,
    return A*np.sin(2*np.pi*k*x+theta)

def residuals(p, y, x):
    """
    实验数据x, y和拟合函数之间的差，p为拟合需要找到的系数
    """
    return y - func(x, p)
x = np.linspace(0, -2*np.pi, 100)
A, k, theta = 10, 0.34, np.pi/6 # 真实数据的函数参数
y0 = func(x, [A, k, theta]) # 真实数据
y1 = y0 + 2 * np.random.randn(len(x)) # 加入噪声之后的实验数据

#numpy.random.randn(d0, d1, …, dn)是从标准正态分布中返回一个或多个样本值。 
#numpy.random.rand(d0, d1, …, dn)的随机样本位于[0, 1)中。 

p0 = [7, 0.2, 0] # 第一次猜测的函数拟合参数
# 调用leastsq进行数据拟合
# residuals为计算误差的函数
# p0为拟合参数的初始值
# args为需要拟合的实验数据
plsq = leastsq(residuals, p0, args=(y1, x))

print (u"真实参数:", [A, k, theta])
print (u"拟合参数", plsq[0] )# 实验数据拟合后的参数

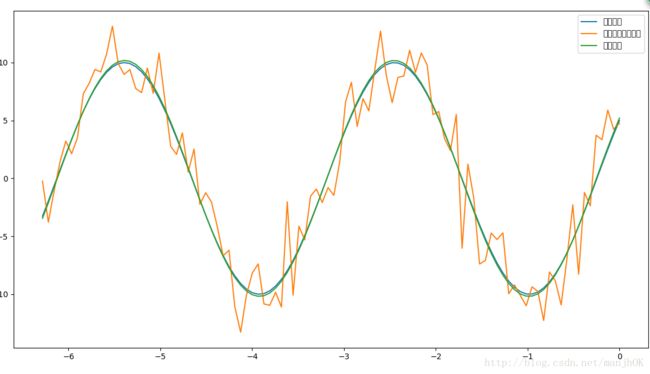
plt.plot(x, y0, label="真实数据")
plt.plot(x, y1, label="带噪声的实验数据")
plt.plot(x, func(x, plsq[0]), label="拟合数据")
plt.legend()
plt.show()

这个例子中我们要拟合的函数是一个正弦波函数，它有三个参数A, k, theta ，分别对应振幅、频率、
相角。假设我们的实验数据是一组包含噪声的数据x, y1，其中y1是在真实数据y0的基础上加入噪声的
到了。
通过leastsq函数对带噪声的实验数据x, y1进行数据拟合，可以找到x和真实数据y0之间的正弦关系的

三个参数： A, k, theta