NNDL 实验六 卷积神经网络(1)卷积
目录
5.1 卷积
5.1.1 二维卷积运算
5.1.2 二维卷积算子
5.1.3 二维卷积的参数量和计算量
5.1.4 感受野
5.1.5 卷积的变种
5.1.6 带步长和零填充的二维卷积算子
5.1.7 使用卷积运算完成图像边缘检测任务
卷积神经网络(Convolutional Neural Network,CNN)
- 受生物学上感受野机制的启发而提出。
- 一般是由卷积层、汇聚层和全连接层交叉堆叠而成的前馈神经网络
- 有三个结构上的特性:局部连接、权重共享、汇聚。
- 具有一定程度上的平移、缩放和旋转不变性。
- 和前馈神经网络相比,卷积神经网络的参数更少。
- 主要应用在图像和视频分析的任务上,其准确率一般也远远超出了其他的神经网络模型。
- 近年来卷积神经网络也广泛地应用到自然语言处理、推荐系统等领域。
5.1 卷积
考虑到使用全连接前馈网络来处理图像时,会出现如下问题:
(1)模型参数过多,容易发生过拟合。 在全连接前馈网络中,隐藏层的每个神经元都要跟该层所有输入的神经元相连接。随着隐藏层神经元数量的增多,参数的规模也会急剧增加,导致整个神经网络的训练效率非常低,也很容易发生过拟合。
(2)难以提取图像中的局部不变性特征。 自然图像中的物体都具有局部不变性特征,比如尺度缩放、平移、旋转等操作不影响其语义信息。而全连接前馈网络很难提取这些局部不变性特征。
卷积神经网络有三个结构上的特性:局部连接、权重共享和汇聚。这些特性使得卷积神经网络具有一定程度上的平移、缩放和旋转不变性。和前馈神经网络相比,卷积神经网络的参数也更少。因此,通常会使用卷积神经网络来处理图像信息。
卷积是分析数学中的一种重要运算,常用于信号处理或图像处理任务。本节以二维卷积为例来进行实践。
5.1.1 二维卷积运算
在机器学习和图像处理领域,卷积的主要功能是在一个图像(或特征图)上滑动一个卷积核,通过卷积操作得到一组新的特征。在计算卷积的过程中,需要进行卷积核的翻转,而这也会带来一些不必要的操作和开销。因此,在具体实现上,一般会以数学中的互相关运算来代替卷积。
在神经网络中,卷积运算的主要作用是抽取特征,卷积核是否进行翻转并不会影响其特征抽取的能力。特别是当卷积核是可学习的参数时,卷积和互相关在能力上是等价的。因此很多时候,为方便起见,会直接用互相关来代替卷积。
![]()
经过卷积运算后,最终输出矩阵大小则为
M′=M−U+1,(5.2)
N′=N−V+1.(5.3)
可以发现,使用卷积处理图像,会有以下两个特性:
1、在卷积层(假设是第层)中的每一个神经元都只和前一层(第层)中某个局部窗口内的神经元相连,构成一个局部连接网络,这也就是卷积神经网络的局部连接特性。
2、由于卷积的主要功能是在一个图像(或特征图)上滑动一个卷积核,所以作为参数的卷积核W\in \mathbb{R} ^{U\times V}对于第层的所有的神经元都是相同的,这也就是卷积神经网络的权重共享特性。
5.1.2 二维卷积算子
算子都继承paddle.nn.Layer飞桨API进行实现,这样我们就可以不用手工写backword()的代码实现。
import torch
import torch.nn as nn
class Conv2D(nn.Module):
def __init__(self, kernel_size, weight_attr=torch.tensor([[0., 1.],[2., 3.]])): # 类初始化,初始化权重属性为默认值
super(Conv2D, self).__init__() # 继承torch.nn.Module中的Conv2D卷积算子
self.weight = torch.nn.Parameter(weight_attr)
def forward(self, X):
u, v = self.weight.shape
output = torch.zeros([X.shape[0], X.shape[1] - u + 1, X.shape[2] - v + 1])
for i in range(output.shape[1]):
for j in range(output.shape[2]):
output[:, i, j] = torch.sum(X[:, i:i+u, j:j+v]*self.weight, dim=[1, 2])
return output
# 随机构造一个二维输入矩阵
torch.manual_seed(100)
inputs = torch.tensor([[[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]])
conv2d = Conv2D(kernel_size=2)
outputs = conv2d(inputs)
print("input: {}, \noutput: {}".format(inputs, outputs))
5.1.3 二维卷积的参数量和计算量
随着隐藏层神经元数量的变多以及层数的加深,
使用全连接前馈网络处理图像数据时,参数量会急剧增加。
如果使用卷积进行图像处理,相较于全连接前馈网络,参数量少了非常多。
参数量
由于二维卷积的运算方式为在一个图像(或特征图)上滑动一个卷积核,通过卷积操作得到一组新的特征。所以参数量仅仅与卷积核的尺寸有关,对于一个输入矩阵![]() 和一个滤波器
和一个滤波器![]() ,卷积核的参数量为
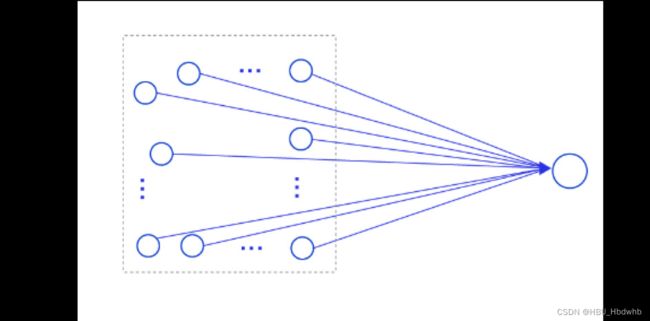
,卷积核的参数量为![]() 。假设有一幅大小为32×32的图像,如果使用全连接前馈网络进行处理,即便第一个隐藏层神经元个数为1,此时该层的参数量也高达1025个,此时该层的计算过程如下图所示。
。假设有一幅大小为32×32的图像,如果使用全连接前馈网络进行处理,即便第一个隐藏层神经元个数为1,此时该层的参数量也高达1025个,此时该层的计算过程如下图所示。
可以想象,随着隐藏层神经元数量的变多以及层数的加深,使用全连接前馈网络处理图像数据时,参数量会急剧增加。如果使用卷积进行图像处理,当卷积核为3×3时,参数量仅为9相较于全连接前馈网络,参数量少了非常多。
计算量
在卷积神经网络中运算时,通常会统计网络总的乘加运算次数作为计算量(FLOPs,floating point of operations),来衡量整个网络的运算速度。对于单个二维卷积,计算量的统计方式为:
FLOPs=M′×N′×U×V。(5.4)
其中M′×N′表示输出特征图的尺寸,即输出特征图上每个点都要与卷积核![]() 进行U×V
进行U×V
次乘加运算。对于一幅大小为32×32的图像,使用3×3的卷积核进行运算可以得到以下的输出特征图尺寸:
M′=M−U+1=30M′=M−U+1=30
N′=N−V+1=30N′=N−V+1=30
此时,计算量为:
FLOPs=M′×N′×U×V=30×30×3×3=8100
5.1.4 感受野
输出特征图上每个点的数值,是由输入图片上大小为U×V的区域的元素与卷积核每个元素相乘再相加得到的,所以输入图像上U×V区域内每个元素数值的改变,都会影响输出点的像素值。我们将这个区域叫做输出特征图上对应点的感受野。感受野内每个元素数值的变动,都会影响输出点的数值变化。比如3×3卷积对应的感受野大小就是3×3,如下图所示。
而当通过两层3×3的卷积之后,感受野的大小将会增加到5×5,如下图所示。
因此,当增加卷积网络深度的同时,感受野将会增大,输出特征图中的一个像素点将会包含更多的图像语义信息。
5.1.5 卷积的变种
在卷积的标准定义基础上,还可以引入卷积核的滑动步长和零填充来增加卷积的多样性,从而更灵活地进行特征抽取。
5.1.5.1 步长(Stride)
在卷积运算的过程中,有时会希望跳过一些位置来降低计算的开销,也可以把这一过程看作是对标准卷积运算输出的下采样。
在计算卷积时,可以在所有维度上每间隔S个元素计算一次,S称为卷积运算的步长(Stride),也就是卷积核在滑动时的间隔。
此时,对于一个输入矩阵![]() 和一个滤波器
和一个滤波器![]() ,它们的卷积为
,它们的卷积为
![]()
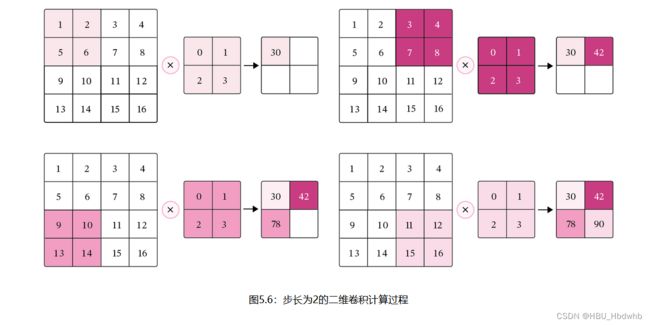
在二维卷积运算中,当步长S=2时,计算过程如下图所示。
5.1.5.2 零填充(Zero Padding)
在卷积运算中,还可以对输入用零进行填充使得其尺寸变大。根据卷积的定义,如果不进行填充,当卷积核尺寸大于1时,输出特征会缩减。对输入进行零填充则可以对卷积核的宽度和输出的大小进行独立的控制。
在二维卷积运算中,零填充(Zero Padding)是指在输入矩阵周围对称地补上P个0。图5.7 为使用零填充的示例。
对于一个输入矩阵![]() 和一个滤波器
和一个滤波器![]() ,,步长为S,对输入矩阵进行零填充,那么最终输出矩阵大小则为:
,,步长为S,对输入矩阵进行零填充,那么最终输出矩阵大小则为:
![]()
![]()
引入步长和零填充后的卷积,参数量和计算量的统计方式与之前一致,参数量与卷积核的尺寸有关,为:U×V,计算量与输出特征图和卷积核的尺寸有关,为:
![]()
一般常用的卷积有以下三类:
1.窄卷积:步长S=1,两端不补零P=0,卷积后输出尺寸为:
M′=M−U+1,
N′=N−V+1.
2.宽卷积:步长S=1,两端补零P=U−1=V−1,卷积后输出尺寸为:
M′=M+U−1,
N′=N+V−1.
3.等宽卷积:步长S=1,两端补零![]() ,卷积后输出尺寸为:
,卷积后输出尺寸为:
M′=M,
N′=N.
通常情况下,在层数较深的卷积神经网络,比如:VGG、ResNet中,会使用等宽卷积保证输出特征图的大小不会随着层数的变深而快速缩减。例如:当卷积核的大小为3×3时,会将步长设置为S=1,两端补零P=1,此时,卷积后的输出尺寸就可以保持不变。在本章后续的案例中,会使用ResNet进行实验。
5.1.6 带步长和零填充的二维卷积算子
引入步长和零填充后,二维卷积算子代码实现如下:
class Conv2D(nn.Module):
def __init__(self, kernel_size, stride=1, padding=0, weight_attr=torch.ones([3, 3])):
super(Conv2D, self).__init__()
self.weight = torch.nn.Parameter(weight_attr)
# 步长
self.stride = stride
# 零填充
self.padding = padding
def forward(self, X):
# 零填充
new_X = torch.zeros([X.shape[0], X.shape[1]+2*self.padding, X.shape[2]+2*self.padding])
new_X[:, self.padding:X.shape[1]+self.padding, self.padding:X.shape[2]+self.padding] = X
u, v = self.weight.shape
output_w = (new_X.shape[1] - u) // self.stride + 1
output_h = (new_X.shape[2] - v) // self.stride + 1
output = torch.zeros([X.shape[0], output_w, output_h])
for i in range(0, output.shape[1]):
for j in range(0, output.shape[2]):
output[:, i, j] = torch.sum(new_X[:, self.stride*i:self.stride*i+u, self.stride*j:self.stride*j+v]*self.weight, dim=[1, 2])
return output
inputs = torch.randn([2, 8, 8])
conv2d_padding = Conv2D(kernel_size=3, padding=1)
outputs = conv2d_padding(inputs)
print("When kernel_size=3, padding=1 stride=1, input's shape: {}, output's shape: {}".format(inputs.shape, outputs.shape))
conv2d_stride = Conv2D(kernel_size=3, stride=2, padding=1)
outputs = conv2d_stride(inputs)
print("When kernel_size=3, padding=1 stride=2, input's shape: {}, output's shape: {}".format(inputs.shape, outputs.shape))从运行结果看出,使用3×3大小卷积,
padding为1,
当stride=1时,模型的输出特征图与输入特征图保持一致;
当stride=2时,模型的输出特征图的宽和高都缩小一倍。
5.1.7 使用卷积运算完成图像边缘检测任务
在图像处理任务中,常用拉普拉斯算子对物体边缘进行提取,拉普拉斯算子为一个大小为3×3的卷积核,中心元素值是8,其余元素值是−1。
考虑到边缘其实就是图像上像素值变化很大的点的集合,因此可以通过计算二阶微分得到,当二阶微分为0时,像素值的变化最大。此时,对x方向和y方向分别求取二阶导数:![]()
![]()
完整的二阶微分公式为:
![]()
上述公式也被称为拉普拉斯算子,对应的二阶微分卷积核为:
![]()
对上述算子全部求反也可以起到相同的作用,此时,该算子可以表示为:
![]()
也就是一个点的四邻域拉普拉斯的算子计算结果是自己像素值的四倍减去上下左右的像素的和,将这个算子旋转45°后与原算子相加,就变成八邻域的拉普拉斯算子,也就是一个像素自己值的八倍减去周围一圈八个像素值的和,做为拉普拉斯计算结果,此时,该算子可以表示为:
![]()
下面我们利用上面定义的Conv2D算子,构造一个简单的拉普拉斯算子,并对一张输入的灰度图片进行边缘检测,提取出目标的外形轮廓。
代码实现
import matplotlib.pyplot as plt
from PIL import Image
import numpy as np
# 读取图片
img = Image.open('小草神.jpg').convert('L')#转成灰度图
img.resize((256,256))
# 设置卷积核参数
w = np.array([[-1,-1,-1], [-1,8,-1], [-1,-1,-1]], dtype='float32')
# 创建卷积算子,卷积核大小为3x3,并使用上面的设置好的数值作为卷积核权重的初始化参数
conv = Conv2D(kernel_size=3, stride=1, padding=0, weight_attr=torch.tensor(w))
# 将读入的图片转化为float32类型的numpy.ndarray
inputs = np.array(img).astype('float32')
print("bf to_tensor, inputs:",inputs)
# 将图片转为Tensor
inputs = torch.tensor(inputs)
print("bf unsqueeze, inputs:",inputs)
inputs = torch.unsqueeze(inputs, dim=0)
print("af unsqueeze, inputs:",inputs)
outputs = conv(inputs)
# 可视化结果
plt.figure(figsize=(8, 4))
f = plt.subplot(121)
f.set_title('input image', fontsize=15)
plt.imshow(img)
f = plt.subplot(122)
f.set_title('output feature map', fontsize=15)
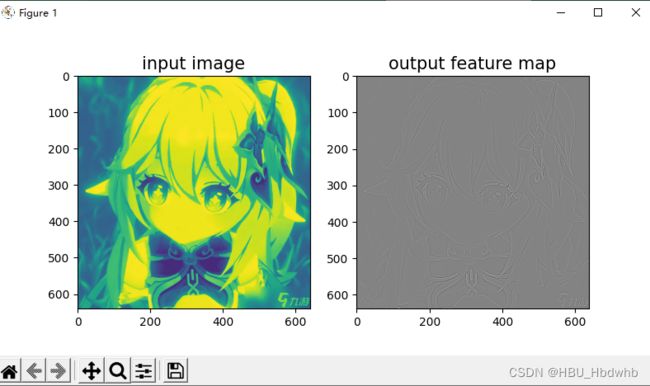
plt.imshow(outputs.detach().numpy().squeeze(), cmap='gray')
plt.savefig('conv-vis.pdf')
plt.show()从输出结果看,使用拉普拉斯算子,目标的边缘可以成功被检测出来。
体会
学习了常见的传统边缘检测的卷积核,并实现了实例化。
参考
NNDL 实验5(上) - HBU_DAVID - 博客园 (cnblogs.com)
五元钱的博客_CSDN博客-深度学习,深度学习作业领域博主