注意力机制详解

Attention机制由来

注意力机制借鉴了人类注意力的说法，比如我们在阅读过程中，会把注意集中在重要的信息上。在训练过程中，输入的权重也都是不同的，注意力机制就是学习到这些权重。最开始attention机制在CV领域被提出来，但后面广泛应用在NLP领域。

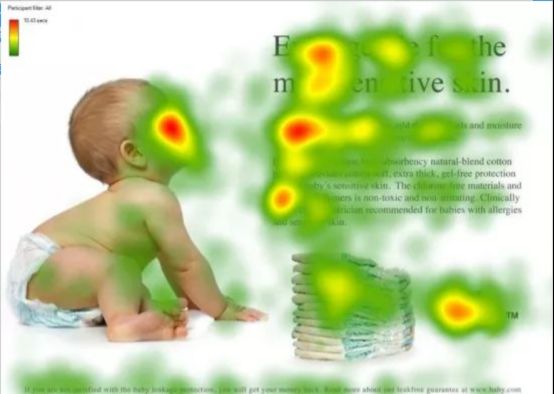
图1形象化展示了人类在看到一副图像时是如何高效分配有限的注意力资源的，其中红色区域表明视觉系统更关注的目标，很明显对于图1所示的场景，人们会把注意力更多投入到人的脸部，文本的标题以及文章首句等位置。

深度学习中的注意力机制从本质上讲和人类的选择性视觉注意力机制类似，核心目标也是从众多信息中选择出对当前任务目标更关键的信息。

Attention定义

Attention的本质就是加权，一般没有严格的定义。
Google 2017年论文Attention is All you need中，为Attention做了一个抽象定义：

An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.
注意力是将一个查询和键值对映射到输出的方法，Q、K、V均为向量，输出通过对V进行加权求和得到，权重就是Q、K相似度。

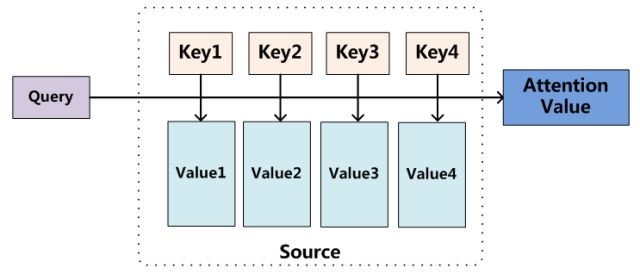
我们可以这样来看待Attention机制：
将Source中的构成元素想象成是由一系列的数据对构成，此时给定Target中的某个元素Query，通过计算Query和各个Key的相似性或者相关性，得到每个Key对应Value的权重系数，然后对Value进行加权求和，即得到了最终的Attention数值。所以本质上Attention机制是对Source中元素的Value值进行加权求和，而Query和Key用来计算对应Value的权重系数。即可以将其本质思想改写为如下公式：
$$\text{ Attention (Query, Source) }=\sum _{i=1}^{L_x}\text{ Similarity }\left(\text{ Query },{\text{ Key }}_i\right)\ast {\text{ Value }}_i$$
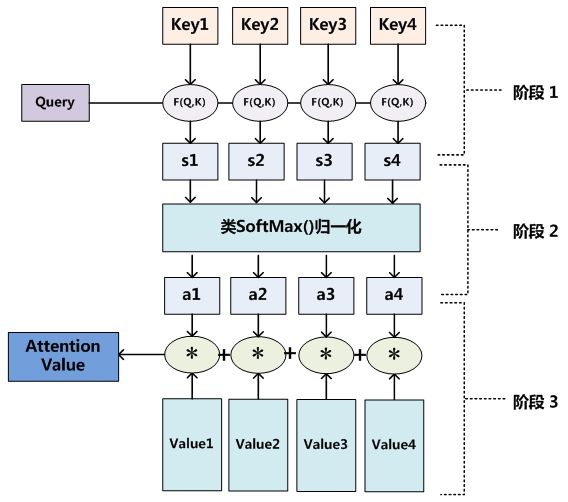
至于Attention机制的具体计算过程，如果对目前大多数方法进行抽象的话，可以将其归纳为三个过程：

• 第一个阶段根据Query和Key计算两者的相似性或者相关性。可以引入不同的函数和计算机制，根据Query和某个Key_i，计算两者的相似性或者相关性，最常见的方法包括：求两者的向量点积、求两者的向量Cosine相似性或者通过再引入额外的神经网络来求值，即如下方式：

  • 点积 ：$\text{ Similarity }\left({\text{ Query, Key }}_i\right)=\text{ Query }\cdot {\text{ Key }}_i$
  • Cosine相似性：$\mathrm{Similarity}\left(\text{ Query, }{\text{ Key}}_i\right)=\frac{Query\cdot Ke{y}_i}{\Vert Query\Vert \cdot \Vert Ke{y}_i\Vert }$
  • MLP网络：$\text{ Similarity }\left(\text{ Query },{\text{ Key }}_i\right)=\text{ MLP }\left({\text{ Query, Key }}_i\right)$

• 第二个阶段对第一阶段的原始分值进行归一化处理；引入类似 SoftMax 的计算方式对第一阶段的得分进行数值转换，一方面可以进行归一化，将原始计算分值整理成所有元素权重之和为1的概率分布；另一方面也可以通过SoftMax的内在机制更加突出重要元素的权重。即一般采用如下公式计算：
  $$a_i=\mathrm{Softmax}\left({\mathrm{Sim}}_i\right)=\frac{e^{{\mathrm{Sim}}_i}}{{\sum }_{j=1}^{L_x}{e}^{\mathrm{Sim}j}}$$

• 第三个阶段根据权重系数对Value进行加权求和。
  $$\text{ Attention(Query, Source) }=\sum _{i=1}^{L_x}{a}_i\cdot {\text{ Value }}_i$$
  通过如上三个阶段的计算，即可求出针对Query的Attention数值，目前绝大多数具体的注意力机制计算方法都符合上述的三阶段抽象计算过程。

Encoder-Decoder框架

要了解深度学习中的注意力模型，就不得不先谈Encoder-Decoder框架，因为目前大多数注意力模型附着在Encoder-Decoder框架下，当然，其实注意力模型可以看作一种通用的思想，本身并不依赖于特定框架，这点需要注意。

Encoder-Decoder框架可以看作是一种深度学习领域的研究模式，应用场景异常广泛。

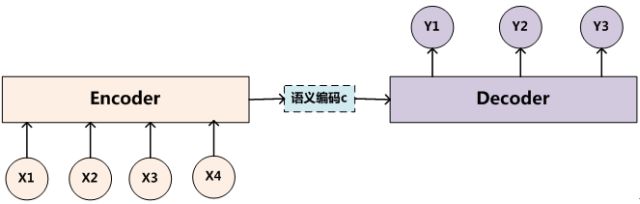
文本处理领域的Encoder-Decoder框架可以这么直观地去理解：
可以把它看作适合处理由一个句子（或篇章）生成另外一个句子（或篇章）的通用处理模型。对于句子对，我们的目标是给定输入句子Source，期待通过Encoder-Decoder框架来生成目标句子Target。Source和Target可以是同一种语言，也可以是两种不同的语言。而Source和Target分别由各自的单词序列构成：
$$\begin{array}{rl}& \text{ Source }=⟨{\mathrm{x}}_1,{\mathrm{x}}_2\dots {\mathrm{x}}_{\mathrm{m}}⟩\\ & \text{ Target }=⟨{\mathrm{y}}_1,{\mathrm{y}}_2\dots {\mathrm{y}}_{\mathrm{n}}⟩\end{array}$$
Encoder顾名思义就是对输入句子Source进行编码，将输入句子通过非线性变换转化为中间语义表示$C$：
$$\mathrm{C}=\mathcal{F}\left({\mathrm{x}}_1,{\mathrm{x}}_2\dots {\mathrm{x}}_{\mathrm{m}}\right)$$
对于解码器Decoder来说，其任务是根据句子Source的中间语义表示 $C$ 和之前已经生成的历史信息来生成 $i$ 时刻要生成的单词 $y_i$。
$${\mathrm{y}}_{\mathrm{i}}=\mathcal{G}\left(\mathbf{C},{\mathbf{y}}_1,{\mathbf{y}}_2\dots {\mathrm{y}}_{\mathrm{i}-1}\right)$$
每个 $y_i$ 都依次这么产生，那么看起来就是整个系统根据输入句子Source生成了目标句子Target。
如果Source是中文句子，Target是英文句子，那么这就是解决机器翻译问题的Encoder-Decoder框架；如果Source是一篇文章，Target是概括性的几句描述语句，那么这是文本摘要的Encoder-Decoder框架；如果Source是一句问句，Target是一句回答，那么这是问答系统或者对话机器人的Encoder-Decoder框架。由此可见，在文本处理领域，Encoder-Decoder的应用领域相当广泛。

Attenion机制的引入

上图展示的Encoder-Decoder框架是没有体现出“注意力模型”的，所以可以把它看作是注意力不集中的分心模型。为什么说它注意力不集中呢？请观察下目标句子Target中每个单词的生成过程如下：
$$\begin{array}{rl}& {\mathbf{y}}_1=\mathbf{f}(\mathbf{C})\\ & {\mathbf{y}}_2=\mathbf{f}\left(\mathbf{C},{\mathbf{y}}_1\right)\\ & {\mathbf{y}}_3=\mathbf{f}\left(\mathbf{C},{\mathbf{y}}_1,{\mathbf{y}}_2\right)\end{array}$$
其中 $f$ 是Decoder的非线性变换函数。从这里可以看出，在生成目标句子的单词时，不论生成哪个单词，它们使用的输入句子Source的语义编码C都是一样的，没有任何区别。

而语义编码C是由句子Source的每个单词经过Encoder编码产生的，这意味着不论是生成哪个单词，$y_1$, $y_2$ 还是$y_3$ ，其实句子Source中任意单词对生成某个目标单词yi来说影响力都是相同的，这是为何说这个模型没有体现出注意力的缘由。

目标句子中的每个单词都应该学会其对应的源语句子中单词的注意力分配概率信息。这意味着在生成每个单词 $y_i$ 的时候，原先都是相同的中间语义表示 $C$ 会被替换成根据当前生成单词而不断变化的$C_i$。理解Attention模型的关键就是这里，即由固定的中间语义表示 $C$ 换成了根据当前输出单词来调整成加入注意力模型的变化的 $C_i$ 。增加了注意力模型的Encoder-Decoder框架理解起来如图所示。

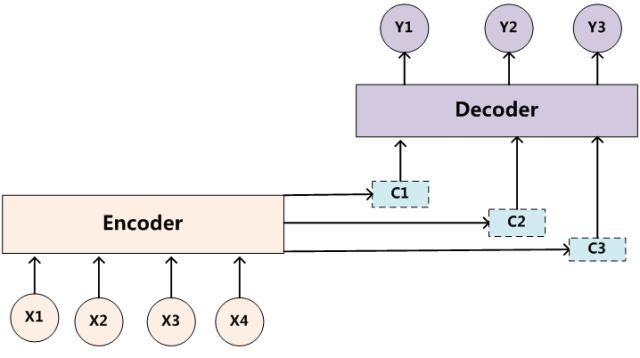
即生成目标句子单词的过程成了下面的形式：
$$\begin{array}{rl}& {\mathbf{y}}_1=\mathbf{f}1\left({\mathbf{C}}_1\right)\\ & {\mathbf{y}}_2=\mathbf{f}1\left({\mathbf{C}}_2,{\mathbf{y}}_1\right)\\ & {\mathbf{y}}_3=\mathbf{f}1\left({\mathbf{C}}_3,{\mathbf{y}}_1,{\mathbf{y}}_2\right)\end{array}$$
如果拿机器翻译来解释，比如输入的是英文句子：Tom chase Jerry，Encoder-Decoder框架逐步生成中文单词：“汤姆”，“追逐”，“杰瑞”。

在翻译“杰瑞”这个中文单词的时候，模型里面的每个英文单词对于翻译目标单词“杰瑞”贡献是不相同的，显然“Jerry”对于翻译成“杰瑞”更重要，如果引入Attention模型的话，应该在翻译“杰瑞”的时候，体现出英文单词对于翻译当前中文单词不同的影响程度，比如给出类似下面一个概率分布值：（Tom,0.3）(Chase,0.2) (Jerry,0.5）

而每个Ci可能对应着不同的源语句子单词的注意力分配概率分布，比如对于上面的英汉翻译来说，其对应的信息可能如下：
$$\begin{array}{rl}& {\mathrm{C}}_{\text{汤姆 }}=\mathrm{g}(0.6\ast \mathrm{f}2(\text{ "Tom" }),0.2\ast \mathrm{f}2(\text{ Chase }),0.2\ast \mathrm{f}2(\text{ "Jerry" }))\\ & {\mathrm{C}}_{\text{追逐 }}=\mathrm{g}(0.2\ast \mathrm{f}2(\text{ "Tom" }),0.7\ast \mathrm{f}2(\text{ Chase }),0.1\ast \mathrm{f}2(\text{ "Jerry" }))\\ & {\mathrm{C}}_{\text{杰瑞 }}=\mathrm{g}(0.3\ast \mathrm{f}2(\text{ "Tom" }),0.2\ast \mathrm{f}2\text{ (Chase), }0.5\ast \mathrm{f}2(\text{ "Jerry" }))\end{array}$$
其中，$f2$ 函数代表Encoder对输入英文单词的某种变换函数，比如如果Encoder是用的RNN模型的话，这个 $f2$ 函数的结果往往是某个时刻输入$x_i$ 后隐层节点的状态值；$g$ 代表Encoder根据单词的中间表示合成整个句子中间语义表示的变换函数，一般的做法中，$g$ 函数就是对构成元素加权求和，即下列公式：
$${\mathbf{C}}_i=\sum _{j=1}^{L_x}{\mathbf{a}}_{ij}{\mathbf{h}}_j$$
翻译中文单词“汤姆”的时候，数学公式对应的中间语义表示 $C_i$ 的形成过程类似下图：

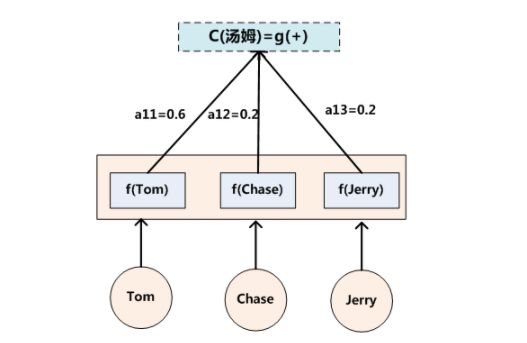
这里还有一个问题：生成目标句子某个单词，比如“汤姆”的时候，如何知道Attention模型所需要的输入句子单词注意力分配概率分布值呢？就是说“汤姆”对应的输入句子Source中各个单词的概率分布：(Tom,0.6)(Chase,0.2)(Jerry,0.2) 是如何得到的呢？

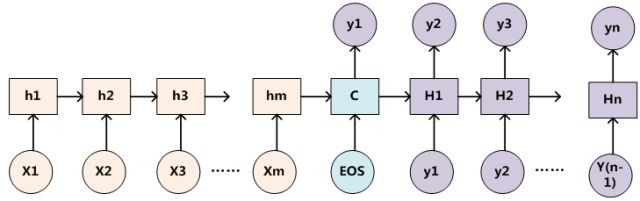
为了便于说明，我们假设对图2的非Attention模型的Encoder-Decoder框架进行细化，Encoder采用RNN模型，Decoder也采用RNN模型，这是比较常见的一种模型配置，则框架转换为下图：

那么用图6可以较为便捷地说明注意力分配概率分布值的通用计算过程。

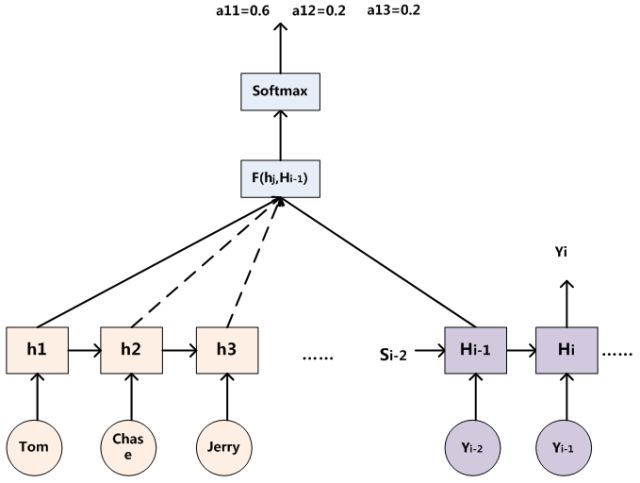
对于采用RNN的Decoder来说，在时刻i，如果要生成 $y_i$ 单词，我们是可以知道Target在生成 $Y_i$ 之前的时刻$i-1$时，隐层节点 $i-1$ 时刻的输出值 $H_{i-1}$ 的，而我们的目的是要计算生成 $Y_i$ 时输入句子中的单词“Tom”、“Chase”、“Jerry”对Yi来说的注意力分配概率分布，那么可以用Target输出句子 $i-1$ 时刻的隐层节点状态 $H_{i-1}$ 去一一和输入句子Source中每个单词对应的RNN隐层节点状态 $h_j$ 进行对比，即通过函数 $F(h_j,H_{i-1})$ 来获得目标单词 $Y_i$ 和每个输入单词对应的对齐可能性，这个 $F$ 函数在不同论文里可能会采取不同的方法，然后函数 $F$ 的输出经过Softmax进行归一化就得到了符合概率分布取值区间的注意力分配概率分布数值。

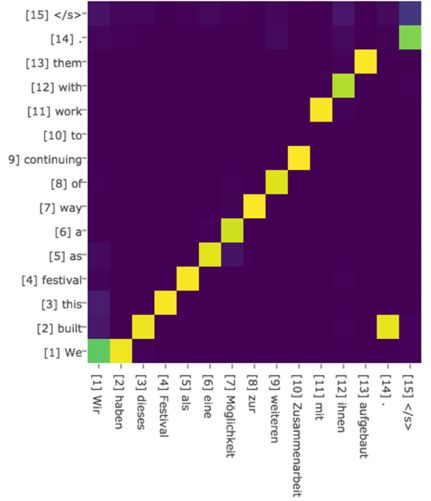
绝大多数Attention模型都是采取上述的计算框架来计算注意力分配概率分布信息，区别只是在F的定义上可能有所不同。图7可视化地展示了在英语-德语翻译系统中加入Attention机制后，Source和Target两个句子每个单词对应的注意力分配概率分布。

Attention机制的类别

根据Attention的计算区域，可以将Attention划分为Hard Attention, Soft Attention, Global Attention 和Local Attention，通俗来说：

• Hard Attention 表示精准定位某个位置，并给该位置的权重赋1，其他都为0，对齐方式要求较高。
• Soft Attention 和Global Attention都表示对所有位置信息计算权重，参考了全局的信息加权，目前大多数Attention机制都是采用这个，但计算量较大。
• Local Attention 表示上面二者的折中，先定位一个窗口，在对窗口内的每个位置计算权重。

同时，Attention Is All You Need 一文又提出了Self Attention 和 Multi-head Attention的概念。

下面对这几种注意力机制进行讲解。

Hard Attention

论文：Show, Attend and Tell：Neural Image Caption Generation with Visual Attention

• 记$s_t$为decoder第 t 个时刻的attention所关注的位置编号
• $s_{ti}$表示第 t 时刻 attention 是否关注位置 i
• $s_{ti}$服从多元伯努利分布(multinoulli distribution)， 对于任意的 t , $s_{ti}$, $i=1,2,...,L$中有且只有取1，其余全部为0，所以$[s_{t1},s_{t2},...,s_{tL}]$是one-hot形式。如翻译任务中，“I have a cat”，对于最后一个时刻（猫）的输出，attention 值为$[0,0,0,1]$，表示只关注最后一个位置cat。
• 存在问题：hard attention不可微分，需要更加复杂的处理，在论文中使用的是蒙特卡洛采样。

Soft Attention

论文：Show, Attend and Tell：Neural Image Caption Generation with Visual Attention

• soft attention每次会照顾到全部的位置，只是不同位置的权重不同。这时$z_t$即为 $a_i$的加权求和 :
  $$z_t=\sum _{i=1}^L{\alpha }_{ti}\ast a_i$$
• 故soft attention是光滑的且可微的（即目标函数，也就是LSTM的目标函数对权重${\alpha }_{ti}$是可微的，原因很简单，因为目标函数对ztzt可微，而$z_t$ 对 ${\alpha }_{ti}$ 可微，根据chain rule可得目标函数对${\alpha }_{ti}$ 可微）。
• 同时可以再做调整，加入${\beta }_t$：
  $$\begin{array}{rl}{z}_t& ={\beta }_t\sum _{i=1}^L{\alpha }_{ti}\ast a_i\\ {\beta }_t& =\sigma \left(f_{\beta }\left(h_{t-1}\right)\right)\end{array}$$
  即根据上一时刻的隐状态决定下一时刻attention相对于$h_{t-1}$和$y_{t-1}$比重
• loss function中还加入了${\alpha }_{ti}$ 的正则项：
  $$L_d=-\log (P(y\mid x))+\lambda \sum _t^C{\left(1-{\alpha }_{ti}\right)}^2$$

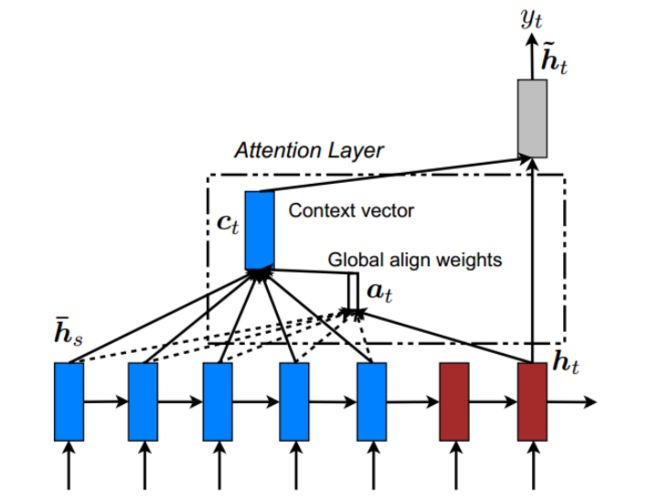
Global Attention

论文：Show, Attend and Tell：Neural Image Caption Generation with Visual Attention

主要思想是考虑所有的编码器的隐藏层状态。

• 记decoder时刻 t 的target hidden为$h_t$ ，encoder的全部hidden state为${\bar{h}}_s$,$s=1,2,...,n$，对于其中任意 ${\bar{h}}_s$，其权重 $a_t(s)$为
  $$a_t(s)=\mathrm{align}\left(h_t,h_s\right)=\frac{\exp \left(\mathrm{score}\left(h_t,h_s\right)\right)}{{\sum }_{s^{\prime }}\exp \left(\mathrm{score}\left(h_t,h_s^{\prime }\right)\right)}$$
  其中，socre是一个基于内容的函数，可以通过如下三个方法实现：
  $$\mathrm{score}\left(h_t,{\bar{h}}_s\right)=\{\begin{array}{ll}{h}_t^{\top }{\bar{h}}_s& \text{ dot }\\ h_t^{\top }{\mathbf{W}}_a{\bar{h}}_s& \text{ general }\\ v_a^{\top }\tanh \left({\mathbf{W}}_a\left[h_t;{\bar{h}}_s\right]\right)& \text{ concat }\end{array}$$
• 通过将所有的整合成一个权重矩阵，得到$Wa$，即可计算得到：
  $$a_t=\mathrm{softmax}\left(W_a{h}_t\right)$$
• 对$a_t$做一个加权平均操作即可得到contex向量$C_t$ ，然后继续进行后续步骤。

Local Attention

论文：Show, Attend and Tell：Neural Image Caption Generation with Visual Attention

主要思想是选择性的关注于上下文所在的一个小窗口，减少计算代价。

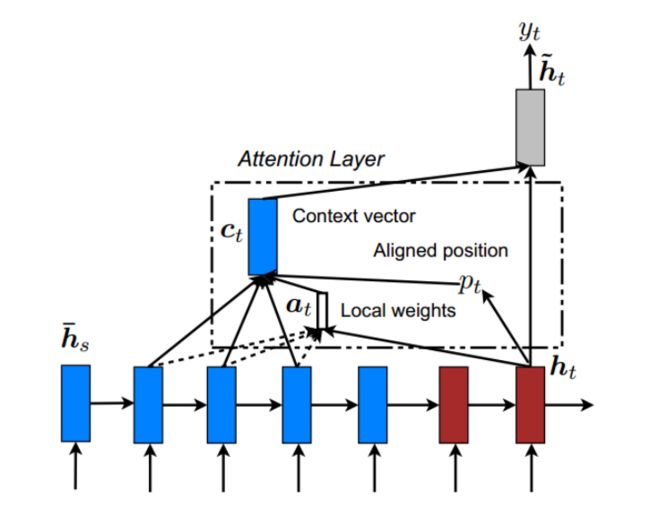
• 对于是时刻 $t$ 的每一个目标词汇，模型首先产生一个对齐的位置（aligned position）$p_t$，context向量 $C_t$ 由编码器中一个集合的隐藏层状态计算得到，编码器中的隐藏层包含在窗口 $[p_t-D,p_t+D]$中，D的大小通过经验选择。
• 因此，global attention和local attention中一个区别就是：前者中对齐向量 $a_t$ 的大小是可变的，大小决定于编码器部分输入序列的长度，而后者中context向量 $a_t$ 的大小是固定的，$a_t\in R^{2D+1}$。文章中提出了模型的两个变种：
  • Monotonic alignment(local-m):
    设置 $p_t=t$，假设源序列和目标序列大致单调对齐，那么对齐向量 可以定义为：
    $$a_t(s)=\mathrm{align}\left(h_t,{\bar{h}}_s\right)=\frac{\exp \left(s\mathrm{core}\left(h_t,{\bar{h}}_s\right)\right)}{{\sum }_{s^{\prime }}\exp \left(\mathrm{score}\left(h_t,h_{s^{\prime }}\right)\right)}$$
  • Predictive alignment(local-p):
    在这种模型中，模型预测了一个对齐位置，而不是假设源序列和目标序列单调对齐。
    $$p_t=S\cdot \mathrm{sigmoid}\left(v_p^T\tanh \left(W_p{h}_t\right)\right)$$
    $W_p$ 和 $v_p$ 是模型的参数，通过训练来预测位置。S是源句子的长度，这样计算之后，$p_t\in [0,S]$。为了支持 $p_t$ 附近的对齐点，设置一个围绕 $p_t$ 的高斯分布，这样，对齐权重就可以表示为：
    $$a_t=\mathrm{align}\left(h_t,{\bar{h}}_s\right)\exp \left(-\frac{{\left(s-p_t\right)}^2}{2{\sigma }^2}\right)$$
    这里的对齐函数和global中的对齐函数相同，其中 $\sigma =\frac{D}{2}$ , $p_t$ 是一个真实的数字，$s$ 在以为中心的窗口中的整数。

Self Attention

论文：attention is all you need

在一般任务的Encoder-Decoder框架中，输入Source和输出Target内容是不一样的，比如对于英-中机器翻译来说，Source是英文句子，Target是对应的翻译出的中文句子，Attention机制发生在Target的元素Query和Source中的所有元素之间。

而Self Attention顾名思义，指的不是Target和Source之间的Attention机制，而是Source内部元素之间或者Target内部元素之间发生的Attention机制，也可以理解为Target=Source这种特殊情况下的注意力计算机制。其具体计算过程是一样的，只是计算对象发生了变化而已，所以此处不再赘述其计算过程细节。

如在翻译任务中，Attention表示在同一个英语句子内单词间产生的联系。

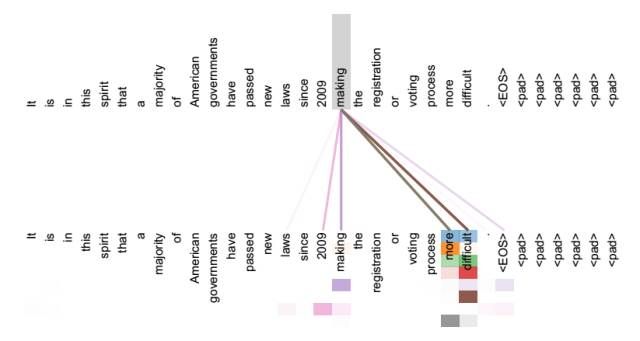
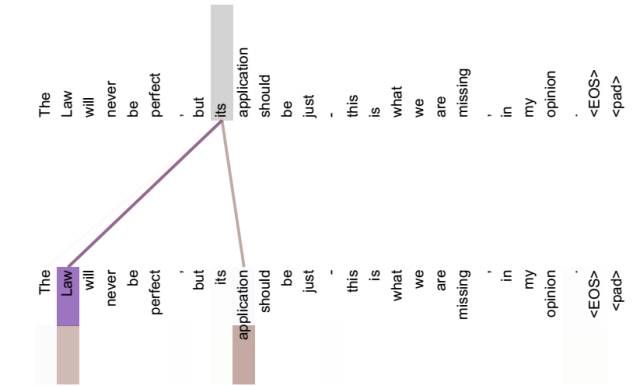
从图中可以看出，Self Attention可以捕获同一个句子中单词之间的一些句法特征（如第一个图中展示的有一定距离的短语结构）或者语义特征（比如第二个图展示的its的指代对象Law）。

很明显，引入Self Attention后会更容易捕获句子中长距离的相互依赖的特征，因为如果是RNN或者LSTM，需要依次序序列计算，对于远距离的相互依赖的特征，要经过若干时间步步骤的信息累积才能将两者联系起来，而距离越远，有效捕获的可能性越小。

但是Self Attention在计算过程中会直接将句子中任意两个单词的联系通过一个计算步骤直接联系起来，所以远距离依赖特征之间的距离被极大缩短，有利于有效地利用这些特征。除此外，Self Attention对于增加计算的并行性也有直接帮助作用，这主要体现在self attention的矩阵计算过程中。这是为何Self Attention逐渐被广泛使用的主要原因。

Multi-head Attention

Multi-head Attention注意力的思想比较直接，把计算Attention的过程重复 $h$ 次，将结果拼接起来就行，以常见的Scaled Dot-Product Attention计算为例：

• 把 Q,K,V 通过参数矩阵映射一下，然后再做 Attention，把这个过程重复做 $h$ 次，每个头的输出为：
  $${\text{ head }}_i=\mathrm{Attention}\left(Q{W}_i^Q,K{W}_i^K,V{W}_i^V\right)$$
  这里$W_i^Q,W_i^K,W_i^V\in R^{d_{\text{mode }}K{d}_k}$
• 将多个头的输出拼接起来：
  $$\mathrm{MultiHead}(\mathbf{Q},\mathbf{K},\mathbf{V})=\text{ Concat }\left({\text{ head }}_1,\dots ,{\text{ head }}_h\right)$$
• 最后得到一个 $n\times (h\tilde{d}v)$ 的序列。所谓“多头”（Multi-Head），就是只多做几次同样的事情（参数不共享），然后把结果拼接。这里如果要生成 $h$ 个平行的Attention，则$d_k=d_{\text{model }}/h$，通过头部维度减少，使得其运算代价仍和单头差不多。

Self attention 和 Multi-head Attention这里只提到其核心思想，具体的运算实现可参考附录中的Transformer。

Attention机制的应用

自然语言处理领域

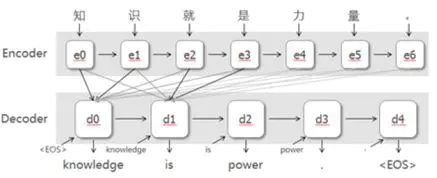
Attention机制在自然语言处理领域有较多的应用，包括以下这几个方向：

• 机器翻译：encoder用于对原文建模，decoder用于生成译文，attention用于连接原文和译文，在每一步翻译的时候关注不同的原文信息。

• 摘要生成：encoder用于对原文建模，decoder用于生成新文本，从形式上和机器翻译都是seq2seq任务，但是从任务特点上看，机器翻译可以具体对齐到某几个词，但这里是由长文本生成短文本，decoder可能需要capture到encoder更多的内容，进行总结。

• 图文互搜：encoder对图片建模，decoder生成相关文本，在decoder生成每个词的时候，用attention机制来关注图片的不同部分。

• 文本蕴含：判断前提和假设是否相关，attention机制用来对前提和假设进行对齐。

• 阅读理解：可以对文本进行self attention，也可以对文章和问题进行对齐。

• 文本分类：一般是对一段句子进行attention，得到一个句向量去做分类。

• 序列标注：Deep Semantic Role Labeling with Self-Attention，这篇论文在softmax前用到了self attention，学习句子结构信息，和利用到标签依赖关系的CRF进行pk。

• 关系抽取：也可以用到self attention

计算机视觉领域

如上图所示，每个例子上方左侧是输入的原图，下方句子是人工智能系统自动产生的描述语句，上方右侧图展示了当AI系统产生语句中划横线单词的时候，对应图片中聚焦的位置区域。比如当输出单词dog的时候，AI系统会将注意力更多地分配给图片中小狗对应的位置。

在计算机视觉的相关应用中大概可以分为两种：

• 学习权重分布：输入数据或特征图上的不同部分对应的专注度不同
  • 这个加权可以是保留所有分量均做加权（即soft attention）；也可以是在分布中以某种采样策略选取部分分量（即hard attention），此时常用RL来做。
  • 这个加权可以作用在原图上，也就是《Recurrent Model of Visual Attention》（RAM）和《Multiple Object Recognition with Visual Attention》（DRAM）；也可以作用在特征图上，如后续的好多文章（例如image caption中的《 Show, Attend and Tell: Neural Image Caption Generation with Visual Attention》)。
  • 这个加权可以作用在空间尺度上，给不同空间区域加权；也可以作用在channel尺度上，给不同通道特征加权；甚至特征图上每个元素加权。
  • 这个加权还可以作用在不同时刻历史特征上，如Machine Translation。
• 任务聚焦：通过将任务分解，设计不同的网络结构（或分支）专注于不同的子任务，重新分配网络的学习能力，从而降低原始任务的难度，使网络更加容易训练。

语音识别领域

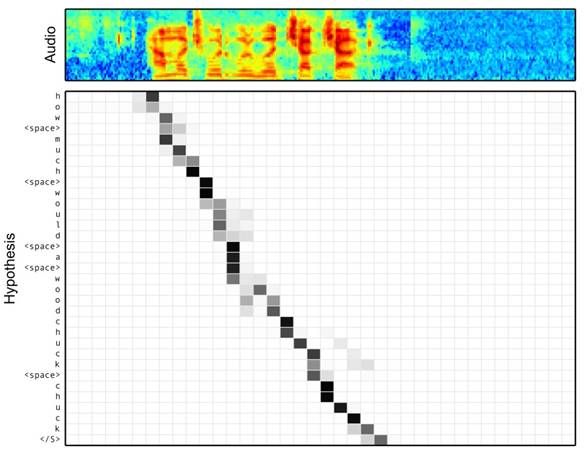
语音识别的任务目标是将语音流信号转换成文字，所以也是Encoder-Decoder的典型应用场景。Encoder部分的Source输入是语音流信号，Decoder部分输出语音对应的字符串流。

上图可视化地展示了在Encoder-Decoder框架中加入Attention机制后，当用户用语音说句子how much would a woodchuck chuck
时，输入部分的声音特征信号和输出字符之间的注意力分配概率分布情况，颜色越深代表分配到的注意力概率越高。从图中可以看出，在这个场景下，Attention机制起到了将输出字符和输入语音信号进行对齐的功能。

图领域

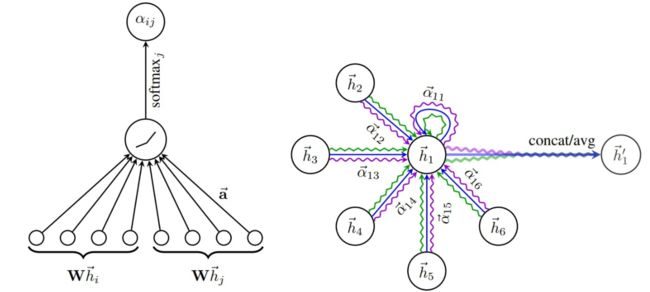
Attention机制在图领域的应用也越来越广泛，主要体现在推荐系统和社交网络等方向上。如 GAT 根据邻居对中心节点重要性的不同，在聚合邻域特征表示时给不同节点分配不同的注意力权重。

附录—Transformer

近年来，随着Transformer的提出，NLP和CV等各个领域都取得了突破性的进展，可以说是万物皆可Transformer, Transformer中有关注意力的部分包括Self Attention 和 Multi-head Attention，主要思想都在上文提及，但运算细节未提及，所以这里作为补充，同学们可根据自身需要选择。

Transformer是在"Attention is All You Need"中提出的，其中的TF应用是Tensor2Tensor的子模块。哈佛的NLP团队专门制作了对应的PyTorch的指南说明。该博客讲解得特别清晰，强烈推荐观看，原文链接

为方便阅读，这里选择了翻译版本进行讲解。

全局视角

我们先将整个模型视为黑盒，比如在机器翻译中，接收一种语言的句子作为输入，然后将其翻译成其他语言输出。

细看下，其中由编码组件、解码组件和它们之间的连接层组成。

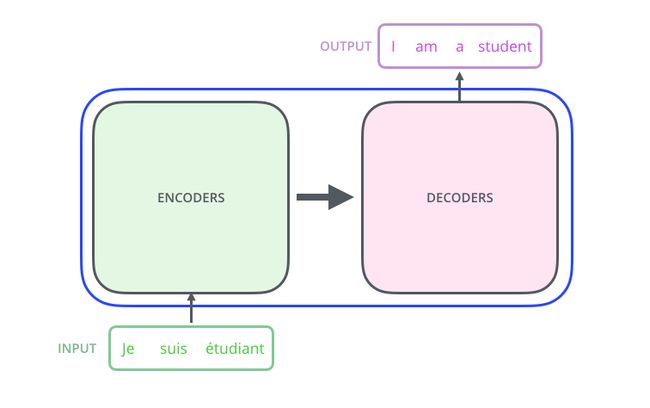
编码组件是六层编码器首位相连堆砌而成，解码组件也是六层解码器堆成的。

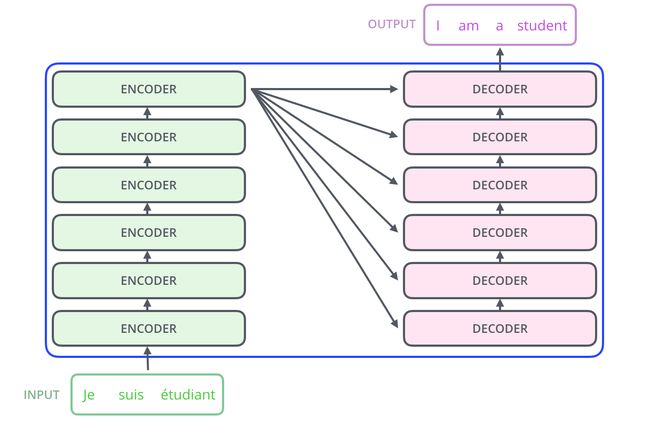
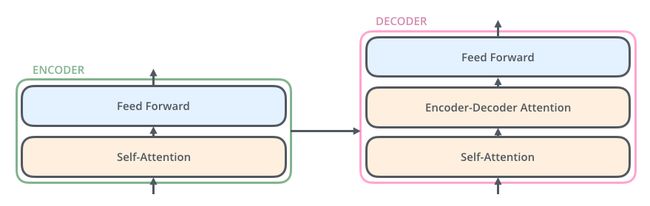
编码器是完全结构相同的，但是并不共享参数，每一个编码器都可以拆解成以下两个部分。

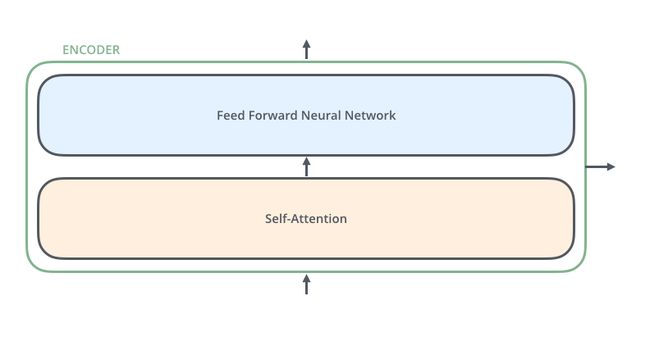
编码器的输入首先流过一个self-attention层，该层帮助编码器能够看到输入序列中的其他单词当它编码某个词时。后面，我们会细看self-attention的内部结构。

self-attention的输出流向一个前馈网络，每个输入位置对应的前馈网络是独立互不干扰的。
解码器同样也有这些子层，但是在两个子层间增加了attention层，该层有助于解码器能够关注到输入句子的相关部分，与 seq2seq model 的attention作用相似。

Tensor视角

现在，我们解析下模型最主要的组件，从Tensor开始，然后是它们如何流经各个组件们并输出的。
正如NLP应用的常见例子，先将输入单词使用embedding 算法转成向量。

词的向量化仅仅发生在最底层的编码器的输入时，这样每个编码器的都会接收到一个list（每个元素都是512维的词向量），只不过其他编码器的输入是上个编码器的输出。list的尺寸是可以设置的超参，通常是训练集的最长句子的长度。
在对输入序列做词的向量化之后，它们流经编码器的如下两个子层。

这里能看到Transformer的一个关键特性，每个位置的词仅仅流过它自己的编码器路径。在self-attention层中，这些路径两两之间是相互依赖的。前馈网络层则没有这些依赖性，但这些路径在流经前馈网络时可以并行执行。

Encoder部分

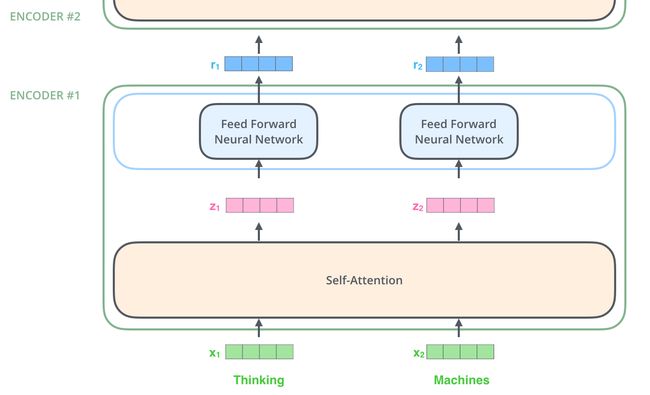
正如之前所提，编码器接收向量的list作输入。然后将其送入self-attention处理，再之后送入前馈网络，最后将输入传入下一个编码器。

Self-Attention

以下面这句话为例，作为我们想要翻译的输入语句“The animal didn’t cross the street because it was too tired”。句子中"it"指的是什么呢？“it"指的是"street” 还是“animal”？对人来说很简单的问题，但是对算法而言并不简单。

当模型处理单词“it”时，self-attention允许将“it”和“animal”联系起来。当模型处理每个位置的词时，self-attention允许模型看到句子的其他位置信息作辅助线索来更好地编码当前词。如果你对RNN熟悉，就能想到RNN的隐状态是如何允许之前的词向量来解释合成当前词的解释向量。Transformer使用self-attention来将相关词的理解编码到当前词中。

上图是Tensor2Tensor notebook的可视化例子

Self-Attention向量计算

我们先看下如何计算self-attention的向量，再看下如何以矩阵方式计算。

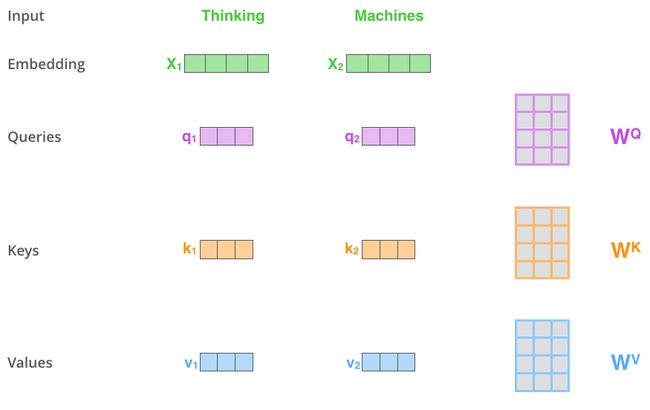
• 第一步，根据编码器的输入向量，生成三个向量，比如，对每个词向量，生成query-vec, key-vec, value-vec，生成方法为分别乘以三个矩阵，这些矩阵在训练过程中需要学习。【注意：不是每个词向量独享3个matrix，而是所有输入共享3个转换矩阵；权重矩阵是基于输入位置的转换矩阵；有个可以尝试的点，如果每个词独享一个转换矩阵，会不会效果更厉害呢？】
  注意到这些新向量的维度比输入词向量的维度要小（512–>64），并不是必须要小的，是为了让多头attention的计算更稳定。
  
• 第二步，计算attention就是计算一个score。对“Thinking Matchines”这句话，对“Thinking”（pos#1）计算attention score。我们需要计算每个词与“Thinking”的score，这个score决定着编码“Thinking”时（某个固定位置时），每个输入词需要集中多少关注度。这个score，通过“Thing”对应query-vector与所有词的key-vec依次做点积得到。所以当我们处理位置#1时，第一个score是q1和k1的点积，第二个score是q1和k2的点积。
  
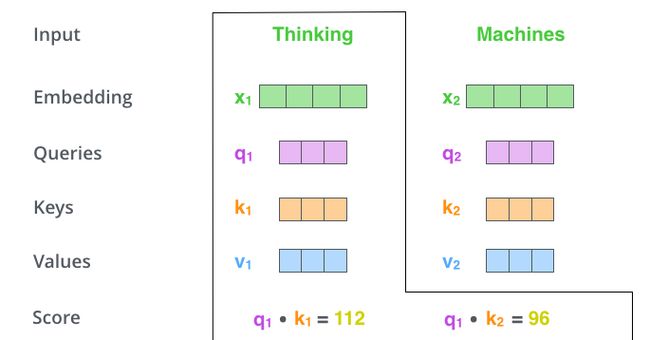
• 第三步和第四步，除以$8=\left(\sqrt{{\text{ dim }}_{key}}\right)$，梯度会更稳定。然后加上softmax操作，归一化score使得全为正数且加和为1。
  
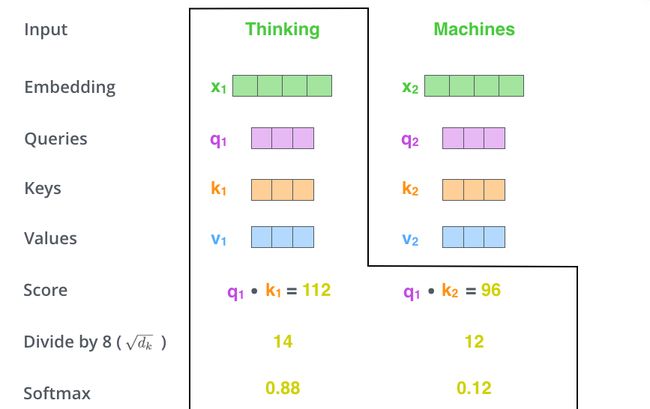
  softmax值决定着在这个位置，每个词的表达程度（关注度）。
• 第五步，将softmax值与value-vec按位相乘。保留关注词的value值，削弱非相关词的value值。
• 第六步，将所有加权向量加和，产生该位置的self-attention的输出结果。
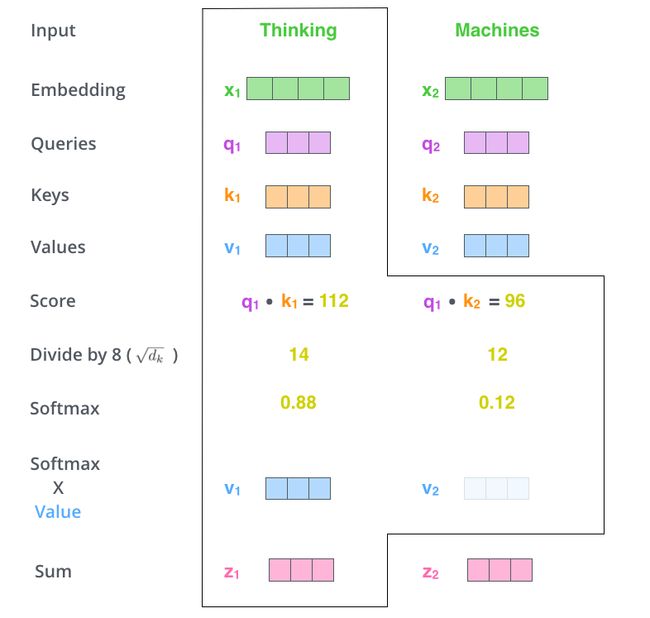  上述就是self-attention的计算过程，生成的向量流入前馈网络。在实际应用中，上述计算是以速度更快的矩阵形式进行的。下面我们看下在词级别的矩阵计算。

Self-Attention的矩阵运算

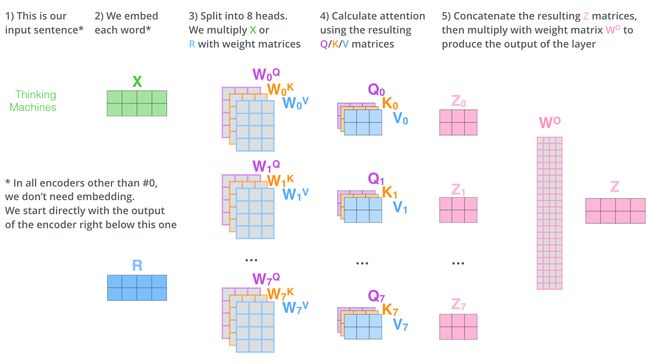
• 第一步，计算query/key/value矩阵，将所有输入词向量合并成输入矩阵$X$，并且将其分别乘以权重矩阵$W^q$ ,$W^k$, $W^v$。
  
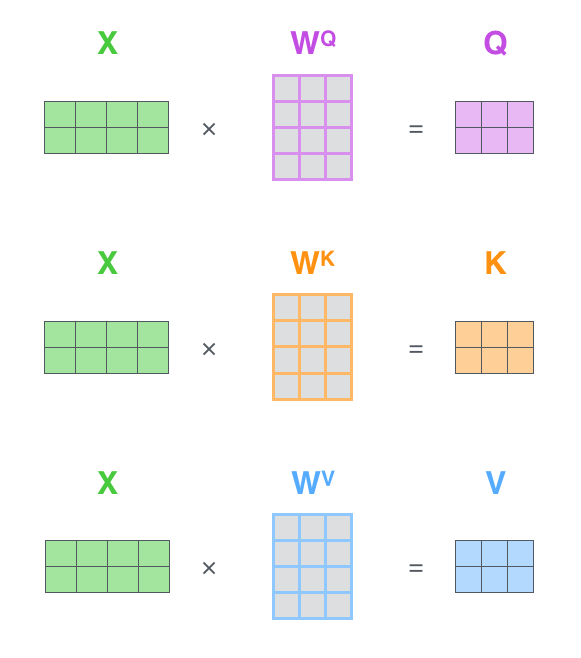
• 最后，鉴于我们使用矩阵处理，将步骤2~6合并成一个计算self-attention层输出的公式。
  

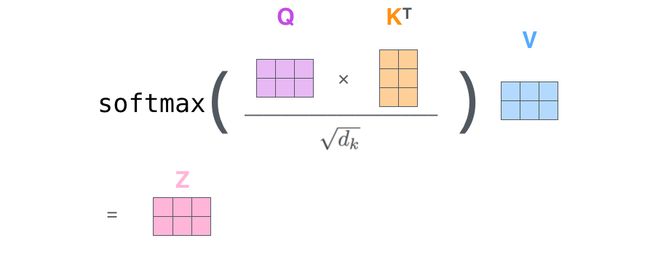
Multi-head Attention

论文进一步增加了multi-head的机制到self-attention上，在如下两个方面提高了attention层的效果：

• 多头机制扩展了模型集中于不同位置的能力。在上面的例子中，$z1$只包含了其他词的很少信息，仅由实际自己词决定。在其他情况下，比如翻译 “The animal didn’t cross the street because it was too tired”时，我们想知道单词"it"指的是什么。
• 多头机制赋予attention多种子表达方式。像下面的例子所示，在多头下有多组query/key/value矩阵，而非仅仅一组（论文中使用8-heads）。每一组都是随机初始化，经过训练之后，输入向量可以被映射到不同的子表达空间中。

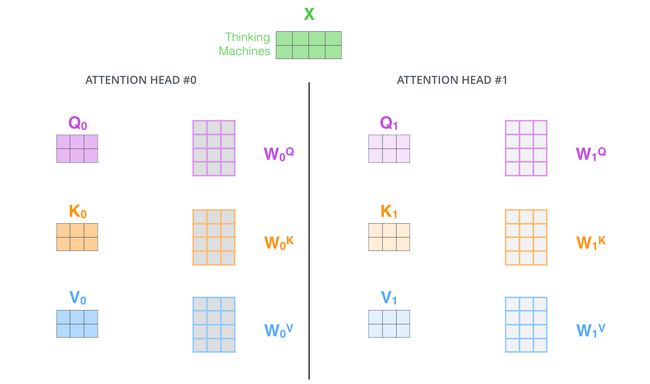
如果我们计算multi-headed self-attention，分别有八组不同的Q/K/V矩阵，我们得到八个不同的矩阵。

这会带来点麻烦，前馈网络并不能接收八个矩阵，而是希望输入是一个矩阵，所以要有种方式处理下八个矩阵合并成一个矩阵。

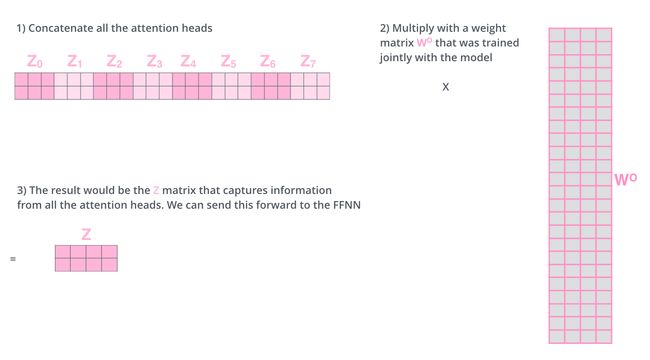
上述就是多头自注意机制的内容，下面尝试着将它们放到一个图上可视化如下：

现在加入attention heads之后，重新看下当编码“it”时，哪些attention head会被集中。

编码"it"时，一个attention head集中于"the animal"，另一个head集中于“tired”，某种意义上讲，模型对“it”的表达合成了的“animal”和“tired”两者如果我们将所有的attention heads都放入到图中，就很难直观地解释了。

Positional Encoding

截止到目前为止，我们还没有讨论如何理解输入语句中词的顺序。
为解决词序的利用问题，Transformer新增了一个向量对每个词，这些向量遵循模型学习的指定模式，来决定词的位置，或者序列中不同词的举例。对其理解，增加这些值来提供词向量间的距离，当其映射到Q/K/V向量以及点乘的attention时。
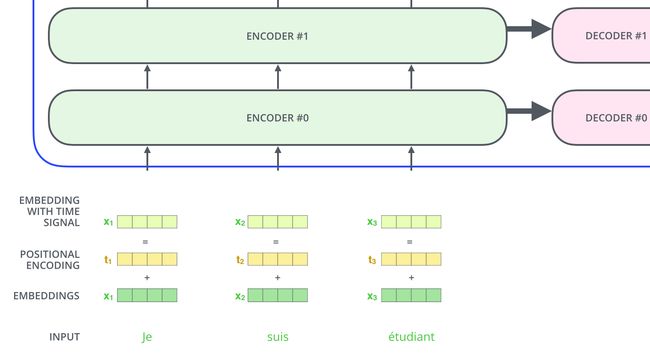如果假设位置向量有4维，实际的位置向量将如下所示：

所谓的指定模式是什么样的呢？
在下图中，每一行表示一个位置的pos-emb，所以第一行是我们将要加到句子第一个词向量上的vector。每个行有512值，每个值范围在[-1,1]，我们将要涂色以便于能够将模式可视化。

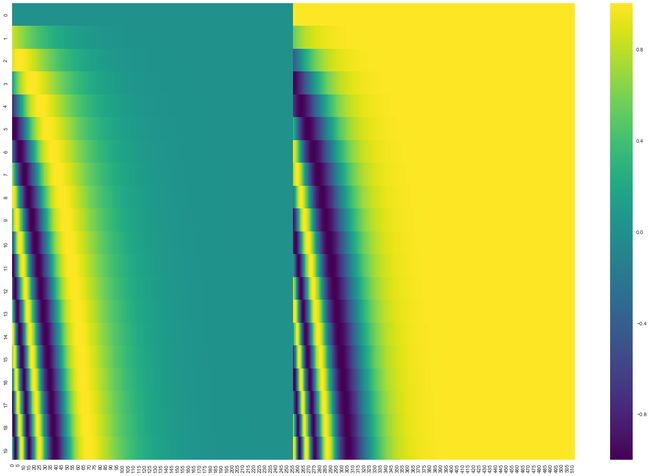
一个真实的例子有20个词，每个词512维。可以观察中间显著的分隔，那是因为左侧是用sine函数生成，右侧是用cosine生成。

位置向量编码方法在论文的3.5节有提到，也可以看代码get_timing_signal_ld()，对位置编码而言并不只有一种方法。需要注意的是，编码方法必须能够处理未知长度的序列。

Residuals

编码器结构中值得提出注意的一个细节是，在每个子层中（self-attention, ffn），都有残差连接，并且紧跟着layer-normalization。

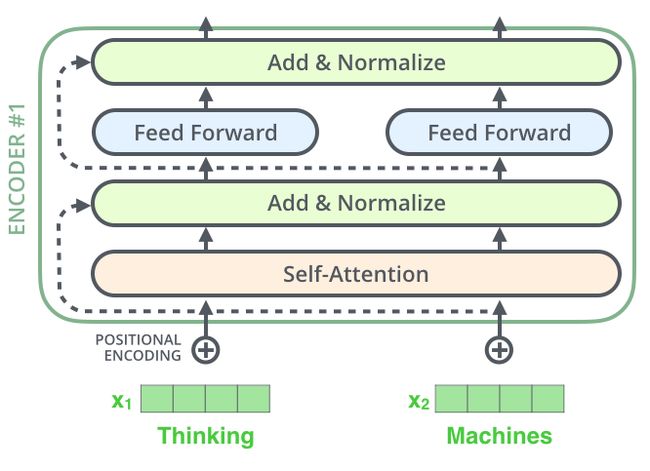
如果我们可视化向量和layer-norm操作，将如下所示：

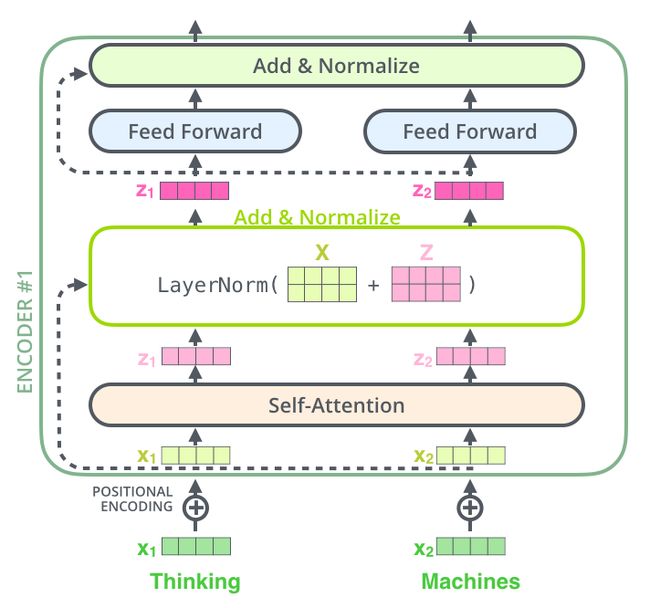
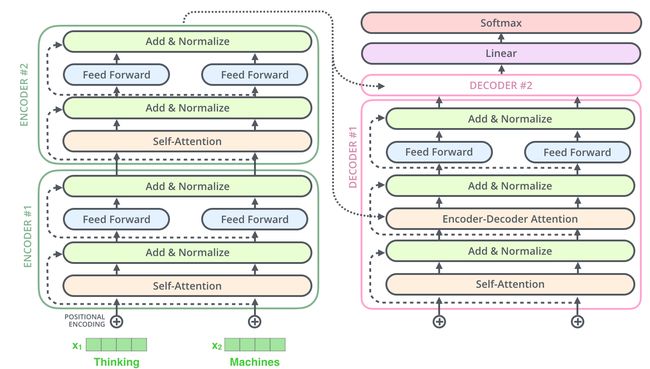
在解码器中也是如此，假设两层编码器+两层解码器组成Transformer，其结构如下：

Decoder部分

现在我们已经了解了编码器侧的大部分概念，也基本了解了解码器的工作方式，下面看下他们是如何共同工作的。
编码器从输入序列的处理开始，最后的编码器的输出被转换为K和V，它俩被每个解码器的"encoder-decoder atttention"层来使用，帮助解码器集中于输入序列的合适位置。

下面的步骤一直重复直到一个特殊符号出现表示解码器完成了翻译输出。每一步的输出被喂到下一个解码器中。正如编码器的输入所做的处理，对解码器的输入增加位置向量。

在解码器中的self attention 层与编码器中的稍有不同，在解码器中，self-attention 层仅仅允许关注早于当前输出的位置。在softmax之前，通过遮挡未来位置（将它们设置为-inf）来实现。

"Encoder-Decoder Attention "层工作方式跟multi-headed self-attention是一样的，除了一点，它从前层获取输出转成query矩阵，接收最后层编码器的key和value矩阵做key和value矩阵。

输出

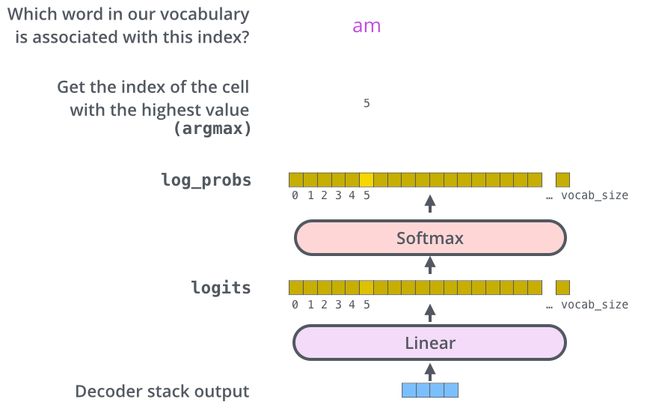
解码器最后输出浮点向量，如何将它转成词？这是最后的线性层和softmax层的主要工作。

线性层是个简单的全连接层，将解码器的最后输出映射到一个非常大的logits向量上。假设模型已知有1万个单词（输出的词表）从训练集中学习得到。那么，logits向量就有1万维，每个值表示是某个词的可能倾向值。

softmax层将这些分数转换成概率值（都是正值，且加和为1），最高值对应的维上的词就是这一步的输出单词。

参考：
深度学习中的注意力模型
attention各种形式总结
Attention机制论文阅读——global attention和local attention
Attention在NLP上的应用
Attention机制【图像】
Attention Is All You Need
The Illustrated Transformer
The Illustrated Transformer【译】