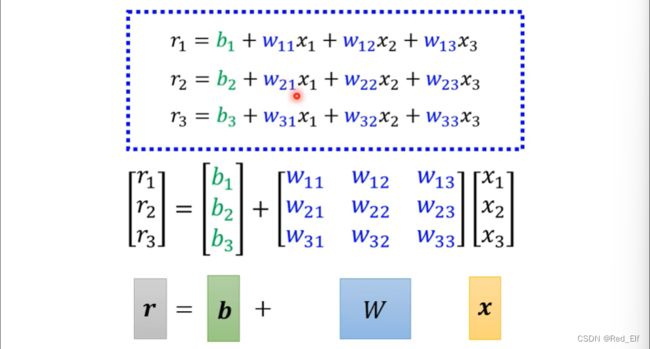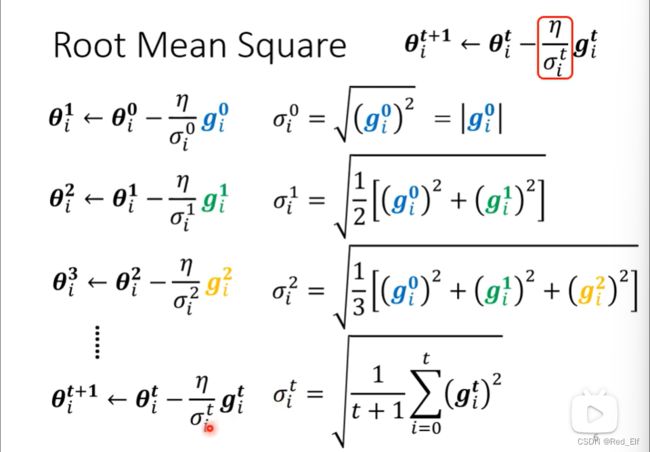李宏毅深度学习笔记——呕心整理版
李宏毅深度学习笔记——呕心整理版
闲谈叨叨叨:
之前看过吴恩达的一部分课程,所以有一定理论基础,再看李宏毅的课程会有新的理解。我先以有基础的情况写完学习过程,后续再以零基础的角度补充细节概念(估计不会啦,因为懒~)。长篇预警!可以慢慢看。多数只是自己的笔记,不会太有语言的概念解释,建议自己看一遍视频(往后字可能会越来越多,听我慢慢叨咕吧)。笔记只是提供回忆、巩固理解的工具。若有问题,欢迎评论讨论,有时间我会改正哒!
经过我多年学习经验(没有啦~),预习真的很重要,其实更多是重复记忆,加深理解。我的建议是先看吴恩达的课程了解机器学习和深度学习的基本知识框架和概念,还有理论推导,理解就可以,这就相当于预习;然后看李宏毅的课程,换个思路,以实际应用加深理解,就会感觉吴恩达的课程缘由不太清楚的自然而然就通了;看李宏毅的课程同时,看刘二大人的pytorch课程,动手操作,学会后完成李宏毅的作业;pytorch需要线性代数和概率论(这些课上要好好学,忘了的可以速学一下考研课程)以及python基础,我会整理一些推荐课程和学习路线。
关于李宏毅课程的视频顺序,我大多是先看2021年,用2022年视频作为补充,快速过一遍,选修部分也看。视频链接还有一位大佬整理的资源我会附在正文的引入部分。
目录附上:
文章目录
- 李宏毅深度学习笔记——呕心整理版
-
- 1 引入
-
- 1.1 机器学习&深度学习
- 1.2 课程规划
- 1.3 机器学习例子
-
- 1.3.1 训练过程(training)
- 1.3.2 改进(很牛逼,建议有基础后回看)
- 1.3.3 激活函数
- 1.3.4 神经网络Neural Network
- 1.4 深度学习简介
-
- 1.4.1 反向传播(back propagation)
- 1.4.2 回归 Regression
- 1.4.3 分类(classification)
- 1.4.4 逻辑回归(Logistic Regression)
- 1.5 Homework
- 2 优化分析
-
- 2.1 局部最小值(local minima)与鞍点(saddle point)
- 2.2 批次(Batch)与动量(Momentum)
- 2.3 自动调整学习率 (Learning Rate)
- 2.4 损失函数(Loss)也会有影响
- 2.5 批次标准化(Batch Normalization)
- 2.6 深度学习
- 3 卷积神经网络(CNN)
-
- 3.1 卷积神经网络(CNN)
- 3.2 Spatial Transformer Layer
- 4 自注意力机制(Self-attention)
-
- 4.1 引入
- 4.2 self-attention
- 4.3 Multi-head Self-attention
- 5 Transformer
正片开始:
1 引入
- 视频资料整理:李宏毅2021&2022机器学习
- 视频:2022-机器学习相关规定
1.1 机器学习&深度学习
机器学习就是寻找一个复杂函数。
深度学习的函数就是类神经网络。
- 函数的输入可以是向量、矩阵、序列等等;
- 函数的输出可以是数值(称为regression 回归)、类别(classification 分类)、文本、图片等等
回归 regression:
分类 classification:
structured learning:
1.2 课程规划
——————————先更新到前5章——————————
Lecture1-5: Supervised Learning 监督学习
训练数据要有标注,数据集要知道输出值
缺点:耗费人工
Lecture 7: Self-supervised Learning
无标注资料——Pre-train
Lecture 6: Generative Adversarial Network(GAN)
Lecture 12: Reinforcement Learning(RL)强化学习
不知道怎么标注
Lecture 8: Anomaly detection 异常检测
Lecture 9: Explainable AI 可解释性AI
Lecture 10: Model attack 模型攻击
Lecture 11: Domain adaptation 域适应
Lecture 13: Network Compression
Lecture 14: life-long learning
Lecture 15: Meta learning
1.3 机器学习例子
- 传送门:
- (上)机器学习基本概念简介
- (下)机器学习基本概念简介
根据过往观看次数预测明天的观看次数
1.3.1 训练过程(training)
-
标签 label:已知的对应结果
求出 e 1 e_1 e1到 e N e_N eN
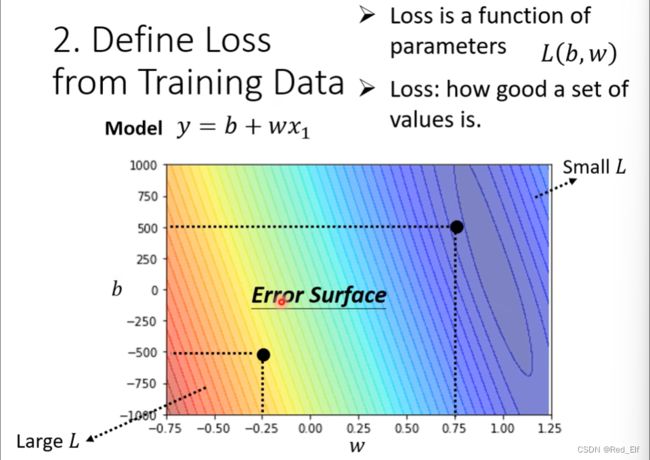
L o s s : L = 1 N ∑ n e n Loss: L=\frac{1}{N}\sum _ne_n Loss:L=N1n∑en误差曲面(error surface):
-
优化
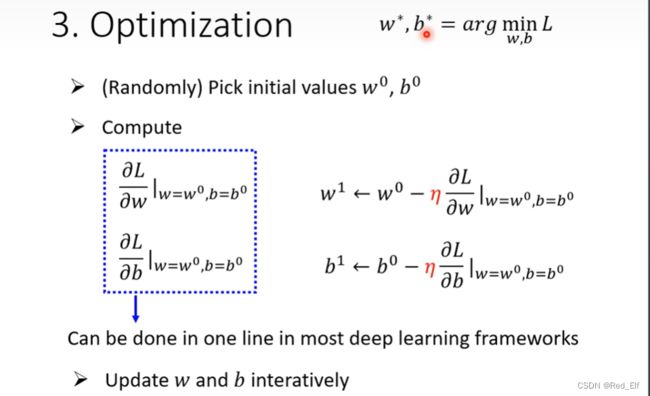
w ∗ , b ∗ = a r g min w , b L w^*, b^* = arg \min_{w,b}L w∗,b∗=argw,bminLa r g m i n argmin argmin:使后面的公式最小的参数
梯度下降 gradient descent
假设只有 w w w一个参数
带上 b b b嘞
超参数(hyper parameter):机器学习中,需要自己设定的参数
学习率
全局最小值与局部最小值的问题。后续补充,在2.1部分(手动跳转吧~ 无法页面内部跳转,气死我啦ヽ(*。>Д<)o゜)
这个问题并不是最主要的,最常见的。其实是学习率!
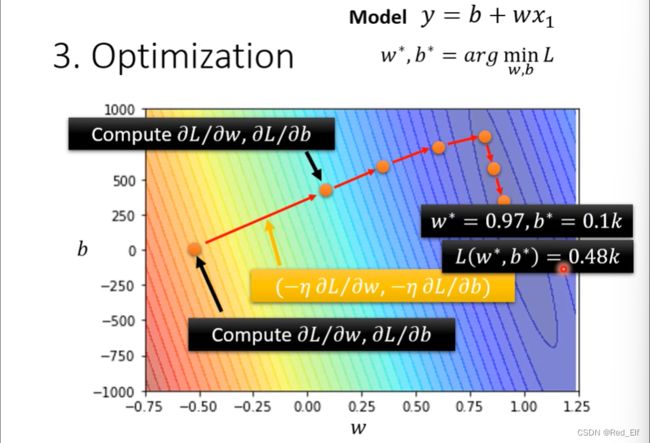
找到使loss最小的 w , b w,b w,b的值
1.3.2 改进(很牛逼,建议有基础后回看)
线性模型太过简单。
model bias:线性模型具有很大的限制
怎么避免model bias?需要更复杂的含有未知参数的函数。
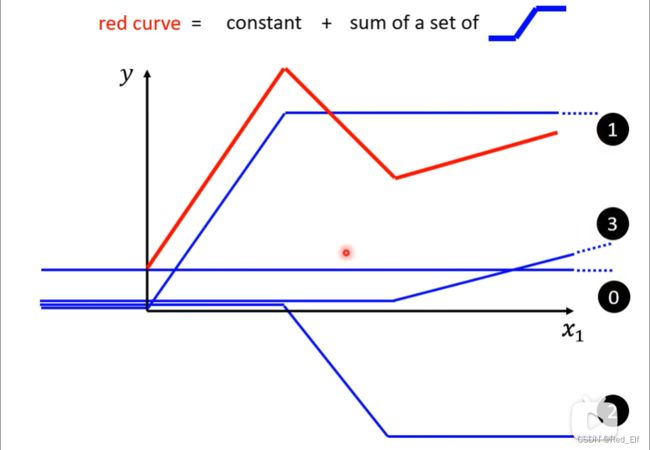
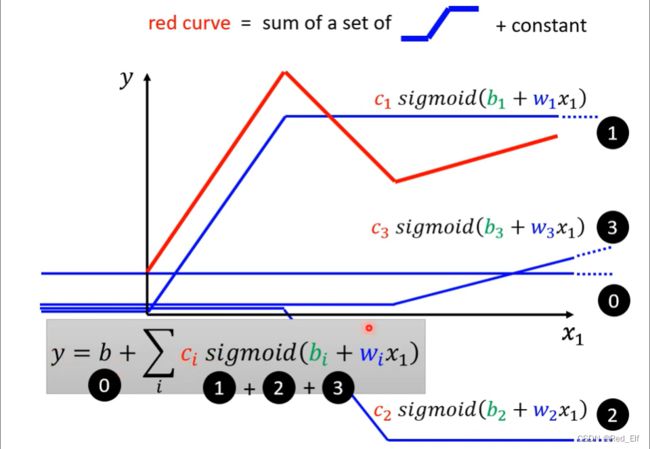
线性函数都可以用一段一段的函数组成,即可用常数+若干个蓝色函数表示。
那怎么表示蓝色函数呢?
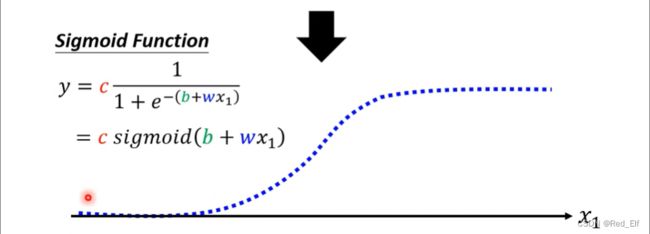
sigmoid function(S函数):
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ y &= c\frac{1}…
调整sigmoid函数的 c , b , w c, b, w c,b,w制作各式各样的蓝色函数
![]()
所以…
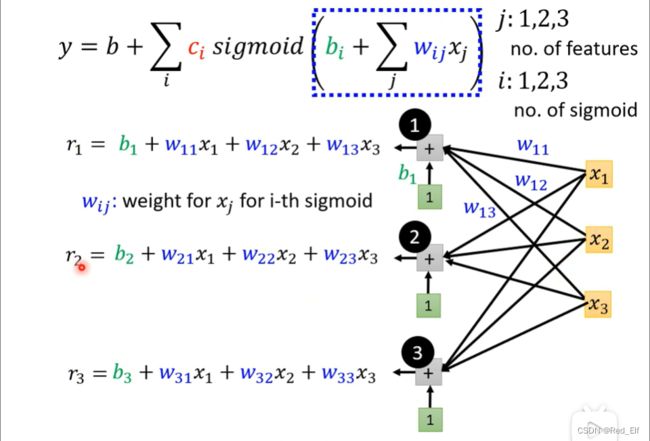
y = b + ∑ i c i s i g m o i d ( b i + w i x 1 ) y=b+\sum_i{c_i\ sigmoid(b_i+w_ix_1)} y=b+i∑ci sigmoid(bi+wix1)
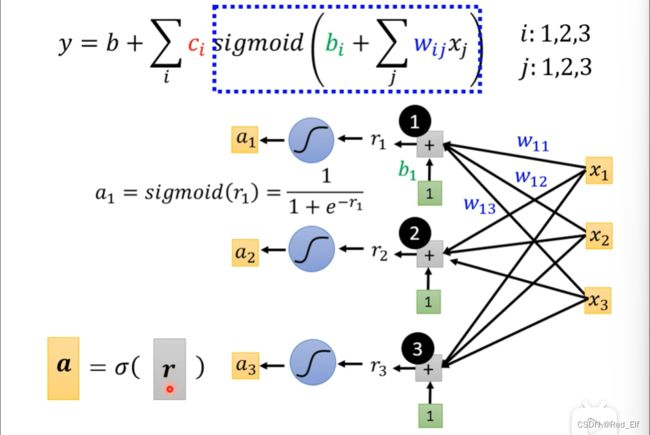
延伸一下(前方高能!!!):
若 y = b + ∑ j w j x j y=b+\sum_j{w_jx_j} y=b+∑jwjxj,则 y = b + ∑ i c i s i g m o i d ( b i + ∑ j w i j x j ) y=b+\sum_i{c_i\ sigmoid(b_i+\sum_j{w_{ij}x_j})} y=b+∑ici sigmoid(bi+∑jwijxj)
绝了哇!!!这不就是神经网络的隐藏层计算嘛!!!
用矩阵表示一下
然后对每个 r r r计算sigmoid
α = σ ( r ) \alpha=\sigma(r) α=σ(r)
最后求y
y = b + c T α y=b+c^T\alpha y=b+cTα

整理一下
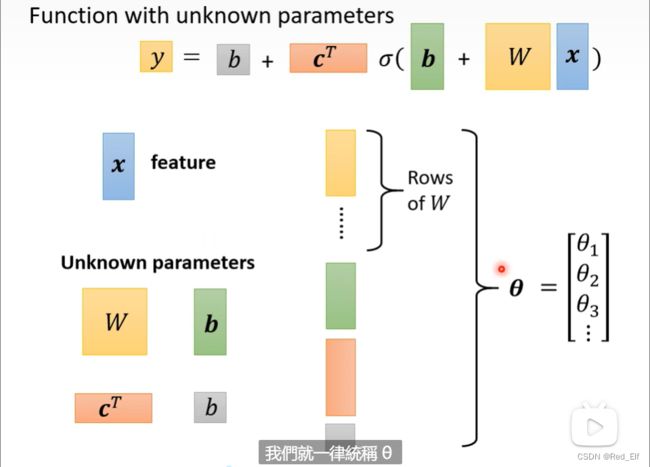
y = b + c T σ ( b + W x ) y = b+c^T\sigma(b+Wx) y=b+cTσ(b+Wx)
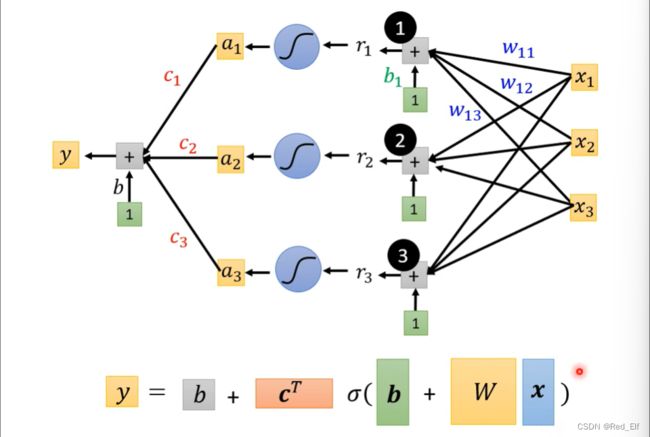
其中 x x x是特征向量(feature), W , b , c T , b W,b,c^T,b W,b,cT,b(注意两个b不是一个意思哦~)是未知参数 ,将未知参数列成一列,统称为 θ \theta θ.
完美,更新了训练过程的第一步!!!
接下来,就是计算loss咯,没有什么变化,只是参数用 θ \theta θ表示,因为参数太多啦。所以loss函数为 L ( θ ) L(\theta) L(θ).
最后是优化,
梯度 gradient。一般不会有梯度为零的情况。
可能数据很多,不方便训练,可以将数据分为几个batch(后续补充,为什么这样做,在2.2部分),用一个batch计算损失值,然后**更新(update)**参数,再选下一个batch,继续更新,直到最后一个batch。
把所有的batch看过一遍,称为一个epoch。
1.3.3 激活函数
ReLU (Rectified Linear Unit)
y = c m a x ( 0 , b + w x 1 ) y=c\ max(0,b+wx_1) y=c max(0,b+wx1)
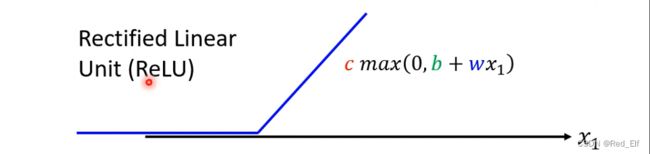
Hard Sigmoid就可以用ReLU组合表示
y = b + ∑ 2 i c i m a x ( 0 , b i + ∑ j w i j x j ) y=b+\sum_{2i}{c_i\ max(0,b_i+\sum_j{w_{ij}x_j)}} y=b+2i∑ci max(0,bi+j∑wijxj)
ReLU、Sigmoid就称为激活函数(activation function)
还有很多激活函数,后续补充…
对于激活函数还有一种解释:
如果都是线性关系,无论有多少层,最后都会化简成一个线性关系式,那前面的那么多层有什么用嘞,所以用激活函数将线性关系转化为非线性关系,让每一层都可以起到提取特征的作用
其实本质上都是让函数更加复杂。
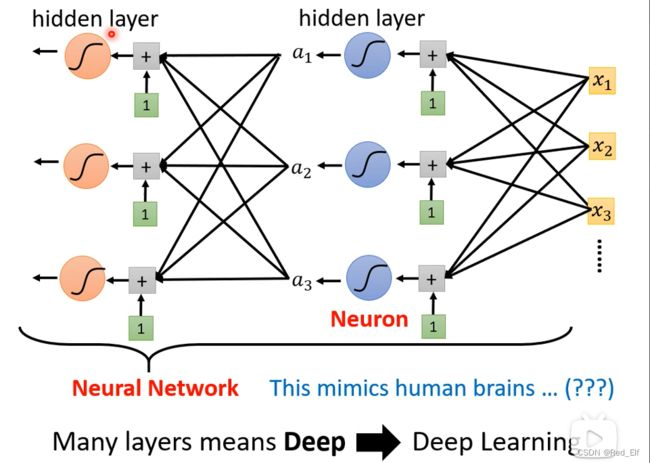
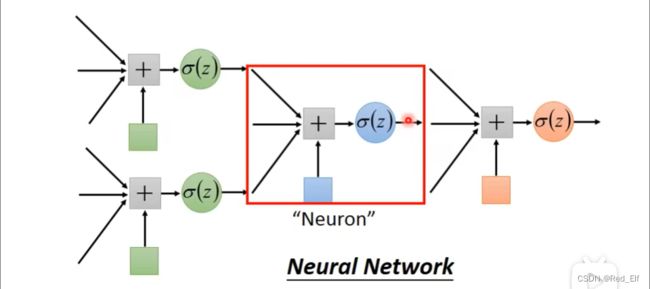
1.3.4 神经网络Neural Network
可以再经历一**层(layer)**计算,层数自己设定,为超参数。
Neuron 神经元
Neural network 神经网络
换个高大上的名字
hidden layer 隐藏层
deep learning 深度学习
之后网络越来越深,贼多层。
但是为什么要更深,而不是更宽呢,后续补充。
越深就越好吗?不是,会出现过拟合(Overfitting),简单来说就是,练习题都会做,全对,一到考试就不会,错的离谱。
1.4 深度学习简介
- 传送门:深度学习简介
全连接前向传播神经网络 Fully connect feedforward network
层数和神经元数的确定,嗯~,靠直觉(经验啦)。当然这个结构也是可以靠自动学习出来的(e.g. evolutionary artificial neural network)
1.4.1 反向传播(back propagation)
- 传送门:反向传播
快速计算梯度的方法而已
链式法则会吧?不会百度一下喽。
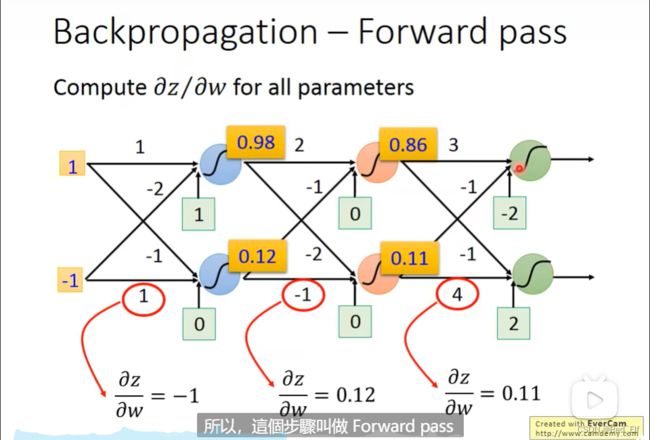
接下来是反向传播求loss值对每个参数的偏导的过程:
局部放大
想求C对w的偏导,是不是可以用链式法则展开一下
∂ C ∂ w = ∂ z ∂ w ∂ C ∂ z \frac{\partial C}{\partial w}=\frac{\partial z}{\partial w}\frac{\partial C}{\partial z} ∂w∂C=∂w∂z∂z∂C
那就分步求呗,先求前面的 ∂ z ∂ w \frac{\partial z}{\partial w} ∂w∂z,用forward pass;再求后面的 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C,用backward pass。
-
Forward pass过程
-
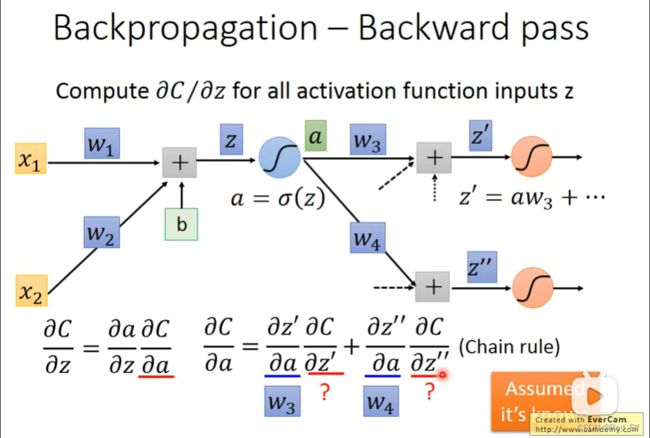
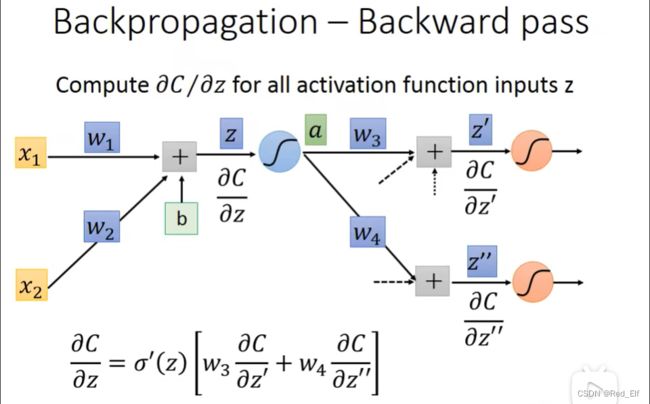
Backward pass过程
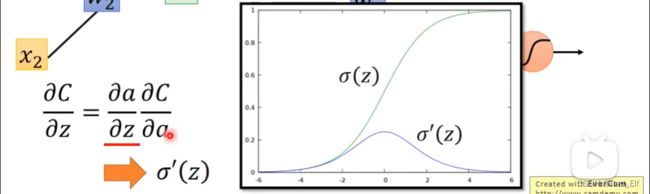
不要忘记中间z到a经历了sigmoid激励函数哦~
∂ a ∂ z = σ ′ ( z ) \frac{\partial a}{\partial z}=\sigma'(z) ∂z∂a=σ′(z)
函数图像是这个样子:好,回到求偏导。那 ∂ C ∂ z ′ \frac{\partial C}{\partial z'} ∂z′∂C和 ∂ C ∂ z ′ ′ \frac{\partial C}{\partial z''} ∂z′′∂C怎么求呢?我们假设已经通过某种方法求出来了
那 ∂ C ∂ z ′ \frac{\partial C}{\partial z'} ∂z′∂C和 ∂ C ∂ z ′ ′ \frac{\partial C}{\partial z''} ∂z′′∂C可以怎么求呢,主要分两种
总结一下反向传播的两个计算过程:
- 用forward pass计算 ∂ z ∂ w = α \frac{\partial z}{\partial w}=\alpha ∂w∂z=α;
- 用backward pass计算 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C
- 两者相乘,即 ∂ C ∂ w = ∂ z ∂ w ∂ C ∂ z \frac{\partial C}{\partial w}=\frac{\partial z}{\partial w}\frac{\partial C}{\partial z} ∂w∂C=∂w∂z∂z∂C
1.4.2 回归 Regression
- 传送门:预测神奇宝贝
著名的宝可梦例子(虽然我不知道宝可梦到底是森么,但是老师举的这种可爱的例子真的很容易理解欸)
基本内容与播放量的例子差不多,有几个补充的点。
-
函数可以是多次式
但是注意【过拟合】的问题。
函数不是越复杂越好,要适合恰当的函数
-
宝可梦的数据与它的种类有关系,意外发现!!!,加上
也有可能存在其他因素对分数有影响,加上
不断的修改函数…
但是其他因素加上后发现,还是存在过拟合的情况,解决办法就是正则化…
-
正则化(regularization)
这其实可以让函数变得平滑,因为w越小,输入的变化对函数的影像就越小,换句话说就是函数不会被输入值所含不确定的因素影响。我们希望得到一个平滑的函数,但是太平滑也不好,loss也会增加。
1.4.3 分类(classification)
- 传送门:分类神奇宝贝
又是宝可梦的例子啦~
其实分类可以理解为回归,比如有两个类别:-1和1,更接近回归结果更接近-1为一类,更接近1为另一类。但不建议实际应用哈。(因为假如是1,2,3类别,1和2是比较像的,到底属于哪个类别并不是很好判断,1和3又不像,所以有时候行,有时候不行,就说明这种方法不建议使用啦。后面会提到如何避免这种情况,在1.4.4的多元分类会提到one-hot vector的方法)
比较好的方法: perceptron;SVM;…(后续再说)
那先用概率的方法研究一下这个问题:
二元分类:两种类别的情况(后续会有多类别分类的例子,在会补充到,不要着急,先把二分类了解个大概)
- 输入属于某一类别的概率:贝叶斯概率公式
- 生成模型 Generative Model:全概率公式
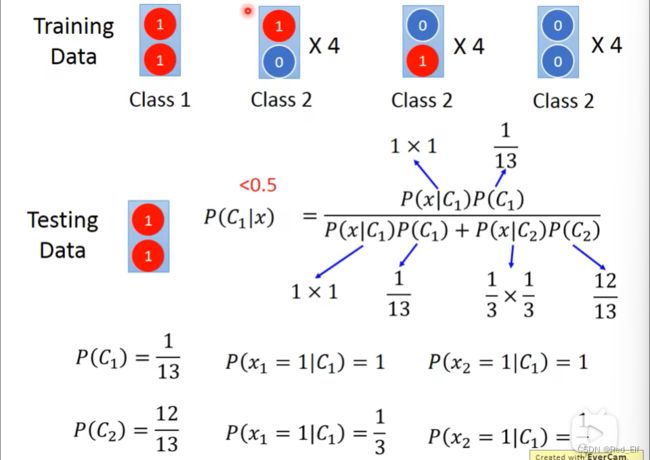
所以要想算这两个值,就得知道四个红框里面 P ( C 1 ) , P ( C 2 ) , P ( x ∣ C 1 ) , P ( x ∣ C 2 ) P(C_1),P(C_2), P(x|C_1),P(x|C_2) P(C1),P(C2),P(x∣C1),P(x∣C2)的数值。
-
首先是 P ( C 1 ) , P ( C 2 ) P(C_1),P(C_2) P(C1),P(C2),这个机率叫做先验 Prior
特征值 feature
-
然后是 P ( x ∣ C 1 ) , P ( x ∣ C 2 ) P(x|C_1),P(x|C_2) P(x∣C1),P(x∣C2)
用高斯分布(正态分布) Gaussion distribution
确定一个高斯分布的重点就是求出 μ , σ \mu,\sigma μ,σ.
怎么求呢,用极大似然法(maximum likelihood)
然后就可以求出属于那一类别的概率了
但是准确率非常低,把所有影响因素加上,也还是很低。
同时,两个种类都有各自的高斯分布,这样参数还是蛮多的。那怎么让参数少一点?共用一个 σ \sigma σ
哦吼,然后把所有因素加上去之后,准确率提升了!!!
好!这个部分就结束掉了。主要是用高斯分布求概率,用贝叶斯概率分类酱紫。
补充一个非常高能的推导——后验概率(Posterior Probability)
没错! P ( C 1 ∣ x ) P(C_1|x) P(C1∣x)化简之后竟然可以写成sigmoid函数。
那我们再来化简以下z。
l n P ( x ∣ C 1 ) P ( x ∣ C 2 ) ln\frac{P(x|C_1)}{P(x|C_2)} lnP(x∣C2)P(x∣C1)咋求捏?
然后,
然后后,
惊不惊喜,意不意外! z = w T x + b z=w^Tx+b z=wTx+b了。回到1.3.2部分的sigmoid函数定义,你说巧不巧。过程看不懂没关系,记住结果就好。
那这就可以解释为,x输入经过z这个函数后,再经历激活函数就得到了输出,即分类的概率。
接下来就引出了逻辑回归的概念,跟上面的例子差不多了啦
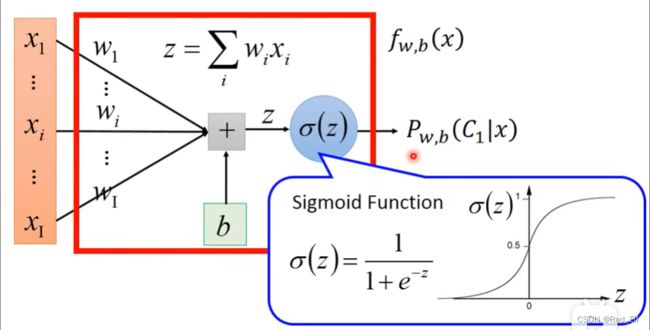
1.4.4 逻辑回归(Logistic Regression)
- 传送门:逻辑回归
注意:这里先以二元分类为例,后续会提到多元分类哒
三个步骤:
-
f w , b ( x ) = P w , b ( C 1 ∣ x ) f_{w,b}(x)=P_{w,b}(C_1|x) fw,b(x)=Pw,b(C1∣x)其实就是后验概率。
画个图理解一下
-
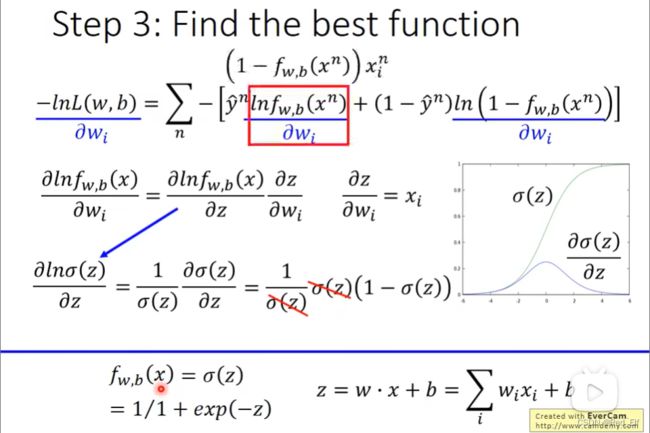
第二步:决定函数的好坏程度
为了计算更容易一点
w ∗ , b ∗ = a r g max w , b L ( w , b ) ⇓ w ∗ , b ∗ = a r g min w , b − l n L ( w , b ) w^*,b^*=arg\ \max_{w,b}{L(w,b)}\\ \Downarrow \\ w^*,b^*=arg\ \min_{w,b}{-lnL(w,b)} w∗,b∗=arg w,bmaxL(w,b)⇓w∗,b∗=arg w,bmin−lnL(w,b)
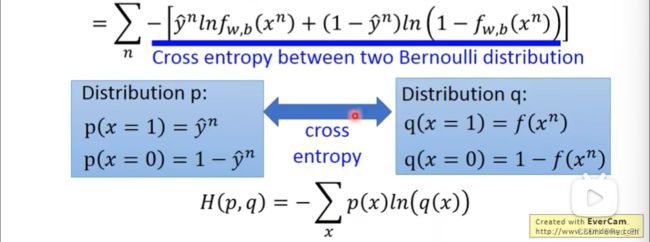
这里定义了 y ^ i \hat{y}^i y^i,就是对应的 x i x^i xi属于哪个类别而已,然后重新表示了 − l n f w , b ( x i ) -lnf_{w,b}(x^i) −lnfw,b(xi)整理一下:
重新定义一下这一大串
C ( f ( x n ) , y ^ n ) = − [ y ^ n l n f ( x n ) + ( 1 − y ^ n ) l n ( 1 − f ( x n ) ) ] C(f(x^n),\hat{y}^n)=-[\hat{y}^nln{f(x^n)}+(1-\hat{y}^n)ln{(1-f(x^n))}] C(f(xn),y^n)=−[y^nlnf(xn)+(1−y^n)ln(1−f(xn))]
所以
L ( f ) = ∑ n C ( f ( x n ) , y ^ n ) L(f)=\sum_n{C(f(x^n),\hat{y}^n)} L(f)=n∑C(f(xn),y^n)拓展:
符合伯努利分布的交叉熵(cross entropy)
如果之前学过吴恩达的课程的话,他的逻辑回归部分中的理论部分就可以理解通了,也清楚这个公式
c o s t ( h θ ( x ) , y ) = − y l o g ( h θ ( x ) ) − ( 1 − y ) l o g ( 1 − h θ ( x ) ) cost(h_\theta(x),y)=-ylog(h_\theta(x))-(1-y)log(1-h_\theta(x)) cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))
是怎么来的了. -
第三步:找到最优秀的function
好滴,那我们把逻辑回归与线性回归做个比较捏~
补充:
为什么逻辑回归不用方差来做loss函数呢?
假如使用方差的话,求偏导后,无论输出值是1还是0,偏导都为0,对收敛起不到效果嘞,毛用没有。
其实这两个是同一个意思:Minimizing cross-entropy is equivalent to maimizing likelihood.
但在分类中,还是建议使用交叉熵。
好了,逻辑回归部分就结束了。
接下来,补充一对概念——判别器(discriminative)和生成器(generative)
-
判别器:逻辑回归的方法,称为discriminative
“判别式模型”是直接建模,并根据某一数据直接预测;
-
生成器:用Gaussian来描述后验概率这件事,成为generative
“生成式模型”是模型先对联合概率分布P(x,y)建模,能够学习出联合概率分布,然后由贝叶斯公式得出条件分布P(y|x),进而进行判断。
判别器和生成器所得参数值是不同的,因为生成器会有很多假设,比如使用的是高斯分布还是其他的概率模型等等。所以他们的回归结果是不同的。所以准确率会有所不同。
很多文献会说判别器的准确率会高于生成器。原因的话,看下面的例子,这个例子是用生成器来判断检验数据是哪一类别。
所得概率居然小于0.5,而实际上人眼判断肯定是class1.为什么会出现这一情况呢?是因为生成器假设这些data来自于一个概率模型,它假设了全1的情况会出现在class2——脑补。而且这个概率也受到data数量的影响。
但其实有时候判别器也不总是高于生成器的:
- 训练数据比较少的时候
- 标签本来就有问题的时候,脑补会避免很多问题
- 先验概率(priors)和类别相关概率(class-dependent probabilities)可以用不同的数据来源预估(没太理解:( )
这一部分,结束掉了。不要着急,还有。
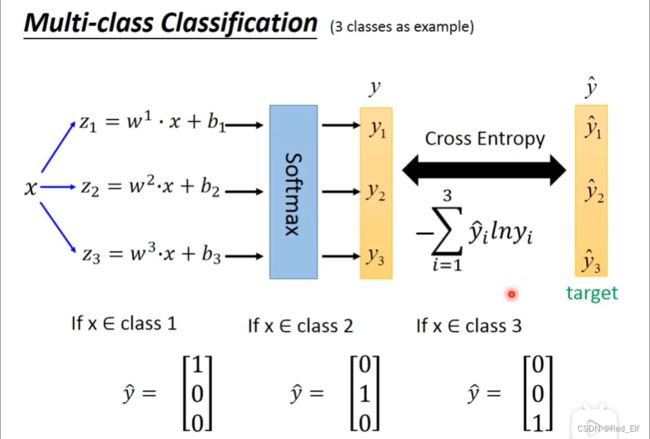
上面的分类都是二分类,那**多分类(multi-class classification)**该怎么办呐?那我们以三分类为例。这里了解过程就好,原理感兴趣就去搜【Bishop,P209-210】部分。
softmax操作(归一化):
- output会介于0~1之间
- output之和为1
这里 y ^ \hat{y} y^用到了one hot(独热编码),这样softmax后就可以判断属于哪个分类的概率了,因为在0-1之间嘛。
然后是Loss函数,这里使用交叉熵,跟上面提到的有点子区别,也很好理解:
e = − ∑ i y i ^ l n y i ′ e=-\sum_i{\hat{y_i}ln{y_i'}} e=−i∑yi^lnyi′
这里不用考虑“1-…”
好,多分类结束!!!
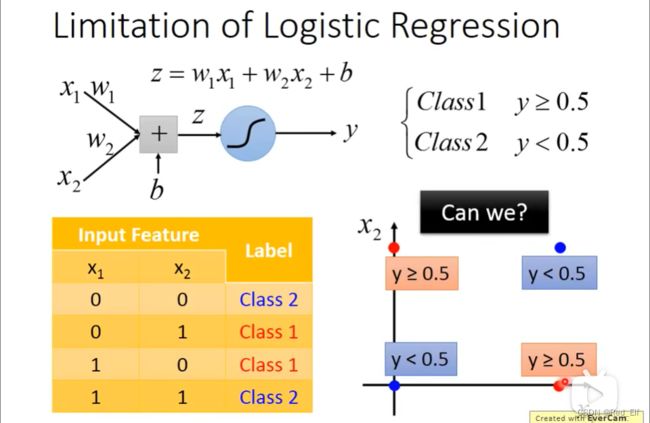
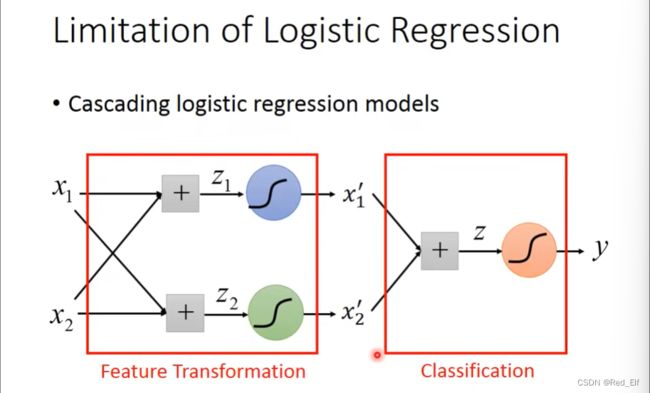
我们再回到逻辑回归。逻辑回归有很强的限制。在某些情况下,普通的逻辑回归并不能做到分类要求,所以需要有所改变。举个例子:
像这样,无论怎样画直线,都不能分出来是class1还是class2. 那怎么办呢?
有两个办法:
-
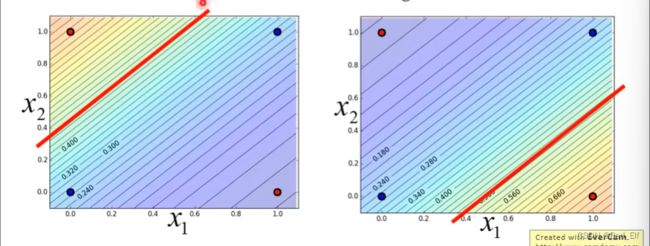
Feature Transformation 特征转换
但是这要怎么进行转换呢?人工!所以这个转换并不能由机器自己产生。所以引出另一个办法 ↓ \downarrow ↓
-
Cascading logistic regression models 级联逻辑回归模型
前方高能!!!这也是神经网络的另一种理解:
x 2 ′ , x 1 ′ x_2',x_1' x2′,x1′画反了,问题不大,理解怎么转换的就好。
好!延伸一下。
把一小个逻辑回归模型视为一个单元,即Neuron。那由多个neuron组成的网络,成为neural network。
逻辑回归结束!!!
1.5 Homework
2 优化分析
这一部分是讨论类神经网络训练得影响因素,训练不起来怎么办?
2.1 局部最小值(local minima)与鞍点(saddle point)
- 传送门: 局部最小值 (local minima) 与鞍点 (saddle point)
这部分分析的问题是如何使梯度下降做得更好。
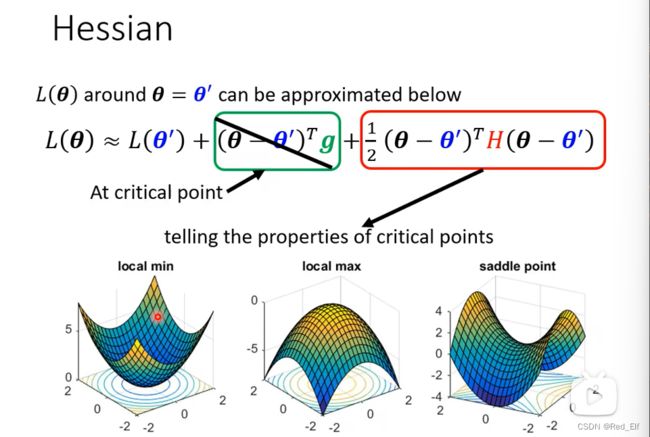
当你训练的时候,很有可能会出现loss一直降不下去。出现这种情况,会发现梯度接近于0了,把这种现象称为梯度消失。好!梯度消失多半在什么位置呢?我们将这些点统称为临界点(critical point),比如:
好!那怎么区分这两个临界点呢?
这就涉及到泰勒展开,浅浅的回顾一下:
Hessian 黑塞(完全没有听过…,问题不大!)
好,当处于临界点时,它的梯度就为0了嘛,所以第二项就没了。那么第三项就是判断临界点种类的依据:
很简单,就是二阶导的问题嘛。把周围所有点带进去求第三项就好了。
- 若第三项都大于零,那就是局部最小值
- 若都小于零,那就是局部最大值
- 若有大于零的,有小于零的,那就是鞍点
但是有亿点麻烦。有个线性代数的方法,可以很快的判断。这涉及到正定矩阵(positive definite),还有特征值(eigen values)(忘记的快快去回忆下)。只要知道特征值的情况,求可以得到H是什么矩阵,继而推出第三项的正负情况。
看不懂?没关系。你只要记住
- 特征值全大于零,局部最小值
- 小于零,局部最大值
- 有正有负,鞍点
好!对于鞍点的情况,我们可以沿着特征向量的方向减小:
但实际上,并不会这么做,因为还要算二次微分,还有特征值之类的,计算量太大,至于还有什么方法去解决,后续会补充。
这里补充一个问题:鞍点和局部最小值那个会更常见呢?
多数的时候鞍点的情况会比较多,而且根据经验来看,得到局部最小值的概率才一半左右,大多数情况都是卡在了鞍点部分。
2.2 批次(Batch)与动量(Momentum)
- 传送门:批次(Batch)与动量(Momentum)
之前有提到过batch,那我们回顾一下:
Shuffle:就是每个epoch中batch的划分是不一样的
接下来回答一下之前提出的问题:为甚么用batch,以及对training的帮助。
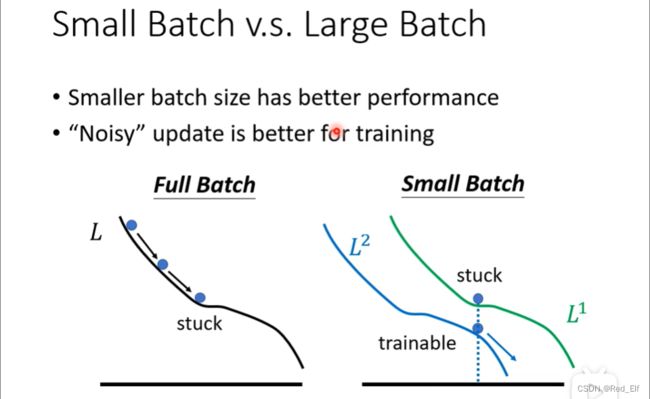
实际操作一下,以两个极端的情况作为例子:没有batch还有batch大小为1
- 没有batch:因为数据太多,所以冷却时间很长,但是稳定
- batch大小为1:因为一次只用1个数据,所以冷却时间短,但是不稳定,噪声很大
其实,大的batch不一定花的时间就多,因为考虑到平行计算的情况。所以时间对于batch大小的选择并不有明显的选择意义。
然而噪声却对训练有所帮助
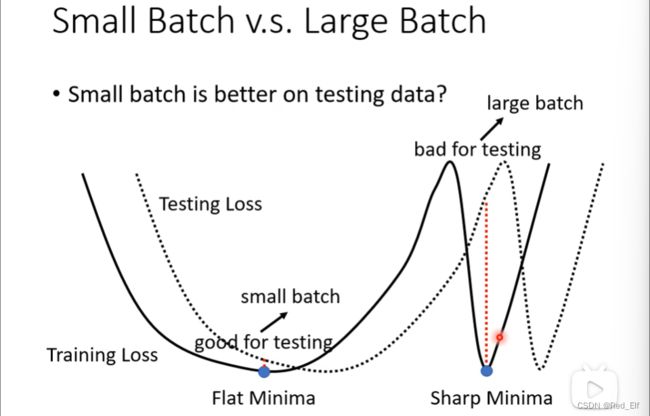
并且小的batch也会对testing有帮助。
局部最小值有好坏之分,峡谷类型(右)就不太友好,因为testing与training的loss函数不一样,会有偏差,峡谷对应的值可能会变化很大,而盆地(左)变化就很小。大的batch很有可能会进入到峡谷当中,因为小的batch方向是不确定的,在遇到峡谷的时候可能会跳出去酱紫。所以小的batch会对testing比较友好。
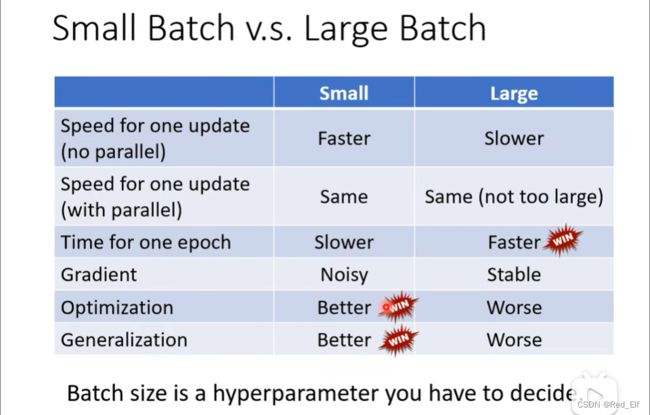
总结一下:
就是说,batch的大小各有优缺点,是个超参数,调参侠上线!
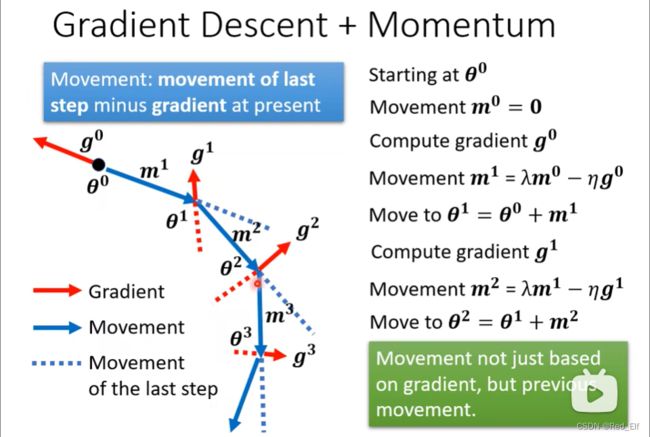
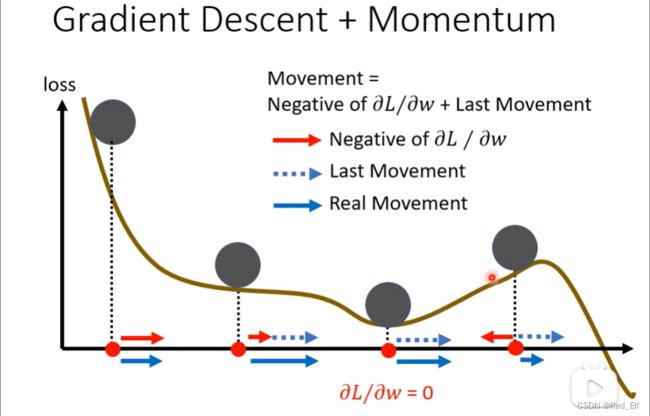
好!Batch部分就到这里。接下来是动量(momentum),他也可以处理saddle point或local minima
其实就是,接下来的运动方向是梯度的反方向与刚刚运动方向的合方向,至于这个系数 λ , η \lambda,\eta λ,η是需要自己去调的。
所以很有可能逃出局部最优解
结束!接下来是学习率的问题。
2.3 自动调整学习率 (Learning Rate)
- 传送门:自动调整学习率 (Learning Rate)
- 如果看不懂下面的公式,可以去看视频。反正建议看!视!频!
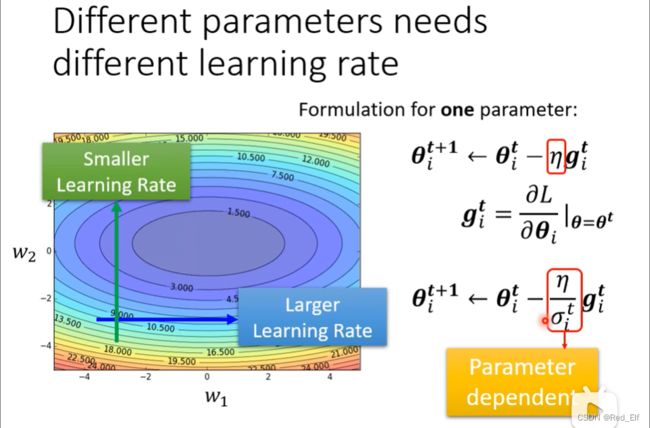
我们在1.3.1的部分有提到过,局部最小值临界点什么的不是最常见的问题,最大的障碍其实是学习率。
有的时候可能根本到不了局部最小值就会卡住,就会出现这种情况:
然而学习率如果只是一个固定的值,效果会不好,所以不同的参数需要不同的学习率。
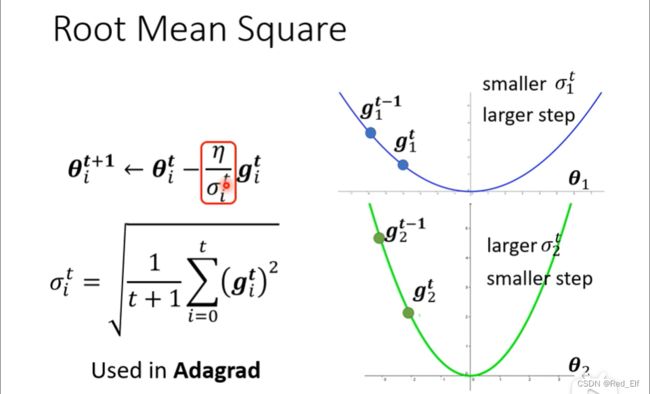
我们需要改变的是:当梯度较小的时候步子可以迈的大一点;而梯度较大的时候步子就迈的小一点。所以学习率就做出一点改变:(这里仅以一个参数为例,实际上每个参数都需要一个学习率的,做法是一样滴)
看一下 η σ i t \frac{\eta}{\sigma^t_i} σitη具体的求法
至于为什么可以做到梯度不同步子不同,很好理解:当坡度较陡那 σ i t \sigma^t_i σit就大,从而 η σ i t \frac{\eta}{\sigma^t_i} σitη就小。
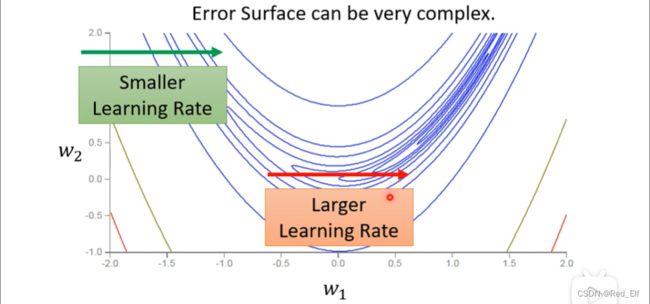
但是这个计算其实是对整体而言,loss的梯度变化比较统一的情况。然而实际上会存在一个loss函数的变化过于复杂,比如这个奇奇怪怪的图:
所以我们需要这个学习率在同一个参数的情况下也可以动态的调整(这里可能会有理解上的矛盾,上面方法的学习率也是动态调整的啊?我的理解是上面的方法是对于整体而言的,整体的梯度小,对于学习率的改变会越大,至于如果有不太统一的变化的情况下,会对学习率不是能么有贡献性,所以我们要引入另外一种算法RMSProp,下面就会给出,看了就明白了)。
![]()
由 α \alpha α来决定梯度的重要性。看个图总结一下:
目前比较流行的优化策略是Adam,久仰大名!其实就是RMSProp和动量的结合,具体的伪代码如下,感兴趣就自己看看吧(不是那么感兴趣hhh),pytorch会写好,直接用就好了。当然有一些参数需要调,但一般默认的就已经很好了。
那我们来看一下不同的方法算学习率后训练的结果
-
用Adagrad的方法
分母累加了太多,导致后面学习率变大,所以出现暴走的状态
-
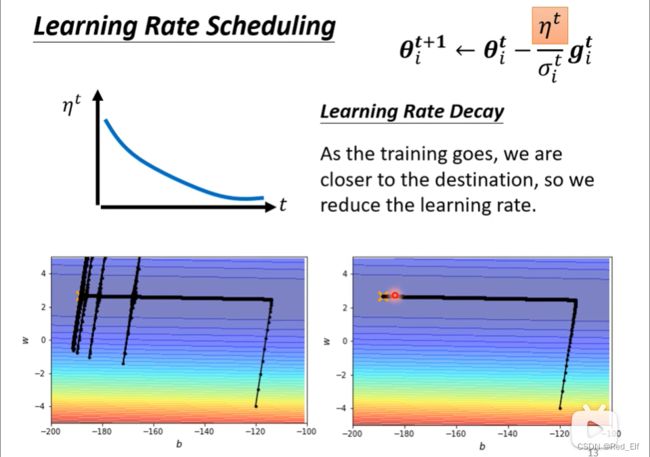
用Learning Rate Scheduling解决暴走状态
第一种方法:让 η \eta η与时间有关( η t \eta^t ηt)就可以解决上面出现的暴走状态。怎么做到与时间有关呢?Learning Rate Scheduling(学习率衰减)。随着时间进行,让 η \eta η不断减小:
第二种方法:Warm UP
至于这个方法的理解,理论说服力没有那么大,个人认为经验至上吧
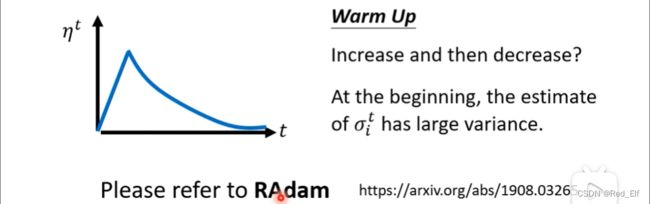
好!这就是学习率优化的部分内容。
那接下来我们要做什么呢?你看我们总会遇到移动不了的情况(不是最优的部分),除了优化学习率,让他走出去,我们可以考虑改变loss,让函数好求一点嘛。
2.4 损失函数(Loss)也会有影响
- 传送门:损失函数(Loss)也会有影响
这个视频课程内容是重复内容,我会直接在前面完善,主要是知识点连上了,会明白为什么要用这个方法,捋清一下思路。可以回看之前的章节加深印象,给个链接:
- 1.4.3的分类
- 1.4.4的one-hot和交叉熵,主要是交叉熵啦
2.5 批次标准化(Batch Normalization)
- 传送门:批次标准化(Batch Normalization)
建议看完卷积网络之后再看这一节,写到这里是为了“合并同类项”而已。可以先跳过,我会在后面提醒你回来的:)
看论文,基本上最后都要跟一个BN,所以来听老师课学习一下。
此处老师给了一个很形象的比喻,BN就是把山铲平的想法(我不是想翻山越岭找到最低点吗,那我给你山铲平咯(怒┗|`O′|┛)
好!我们一点一点来理解。
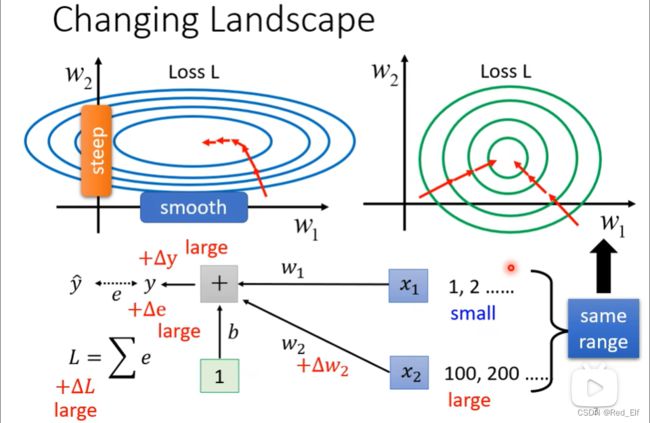
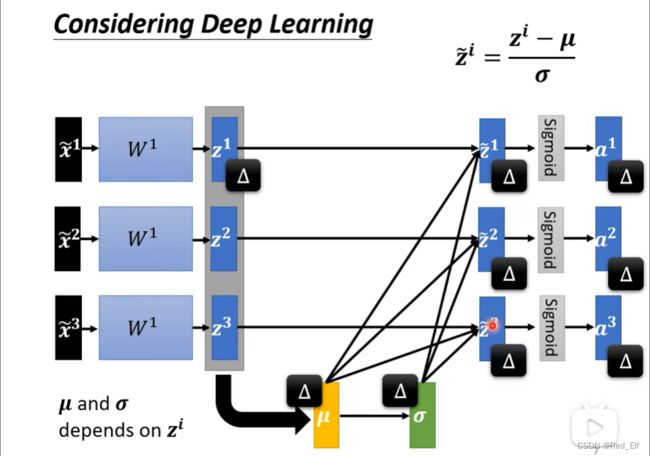
首先,先引入一个概念Feature Normalization(特征归一化)
看上面椭圆形的图,假如 w 1 , w 2 w_1,w_2 w1,w2斜率变化差别非常大,如果lr固定,那很难得到好的结果。看这张图下面的流程图,我们想要 w w w改变找到loss的最小值对不对,但是 w 1 , w 2 w_1,w_2 w1,w2的变化率差距很大。所以怎么样才能减小 w w w对loss变化的影响呢,或者说让loss变化更加平稳均匀呢?那么就和 x x x有关了, x x x很小(大),那 Δ w ∗ x \Delta w*x Δw∗x就小(大),那 Δ L \Delta L ΔL就小(大),所以x的变化程度影响了loss的变化程度。那就让每个x规定在相同的数值范围不就好了嘛!
怎么做到呢?方法有很多,统称为Feature Normalization(特征归一化),下面举一个常用的例子:
好!这是对输入进行特征归一化,但是要是有多层的学习呢,输入是不是也包括上一层的输出,输出的值是不是也会有范围的差距,那这是不是也可以归一化。
(这里激活之前之后都可以实验证明,结果差距不是很大,我们以激活前为例)
求法还和上面一样,然后我们来分析一下变化情况,看下面的图, z 1 z^1 z1变换, μ , σ \mu,\sigma μ,σ就变化,从而后面所有的值都会变化。换句话说,因为归一化,让输入的彼此又有了联系。是不是很妙啊!
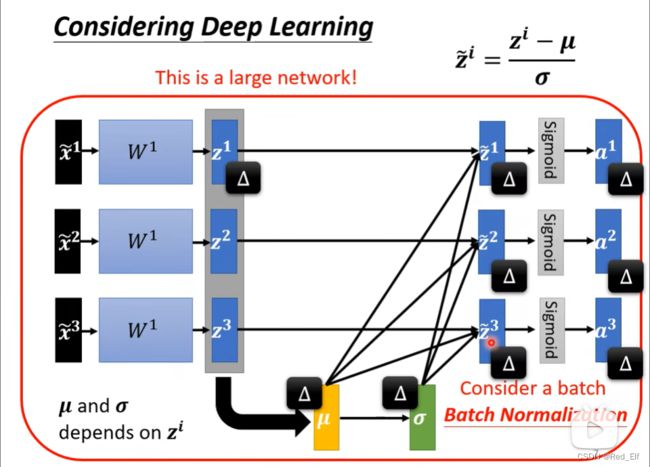
接下来回收题目,Batch Normalization!
假如数据非常庞大,前面讲过是不是可用Batch啊。那我们可以在每个Batch中做归 一化,这就是BN了。但是前提是Batch要够大,才能算 μ \mu μ和 σ \sigma σ,要是1那还算什么hhhh
2.6 深度学习
之前一直都是很简单的一层网络举例子,可能逻辑回归会涉及到一点多层网络。那接下来就理解一下深度学习,其实就是加了几个隐藏层而已,主要是理解为什么要增加层数。
- 传送门:2022-再探宝可梦、数码宝贝分类器 — 浅谈机器学习
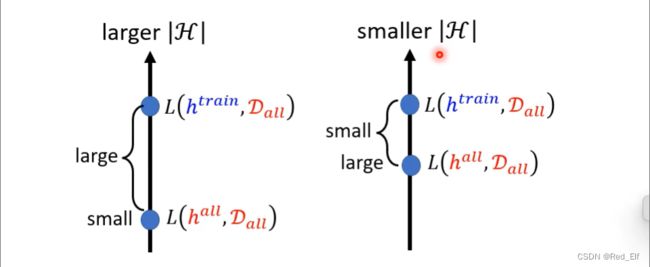
模型的复杂性:
含有未知数的function里面的选择性很多,就叫复杂性很大
想让训练的结果接近现实情况,那训练数据集的要求就是可以代表整个数据集,怎么做到呢
- 数据多一点
- 让参数的选择少一点
但是有了一个两难的境地,如何在数据量比较少的情况下,得到比较低的loss
解决办法就是深度学习
传送门:鱼与熊掌可以兼得的机器学习
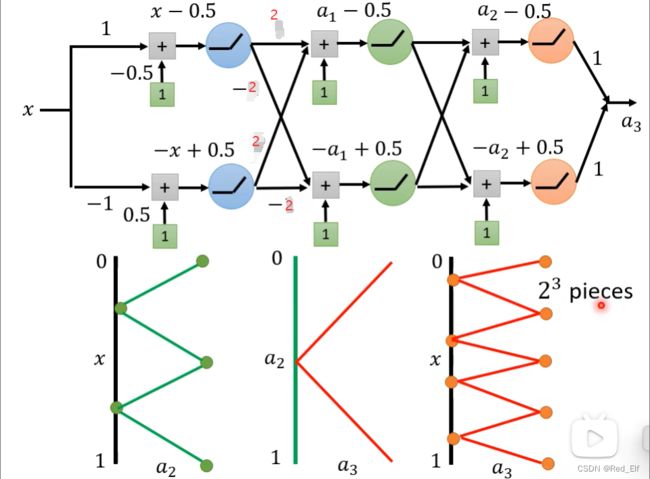
这一节其实讲的就是deep要比shallow的function更有优势,所以深度学习同等条件下比浅层的网络效果更好。
下面是我觉得是对深度学习理解很有帮助的截图,看不懂的建议去看一下视频里老师的讲解。
我说一下我的理解,其实建立神经网络的过程就是想办法去拟合某一个复杂的函数。浅层的网络可以增加很多神经元去一部分一部分的构造,深层的网络可以以指数级的改变函数形状。
3 卷积神经网络(CNN)
重点啊!!!
3.1 卷积神经网络(CNN)
- 传送门:卷积神经网络CNN
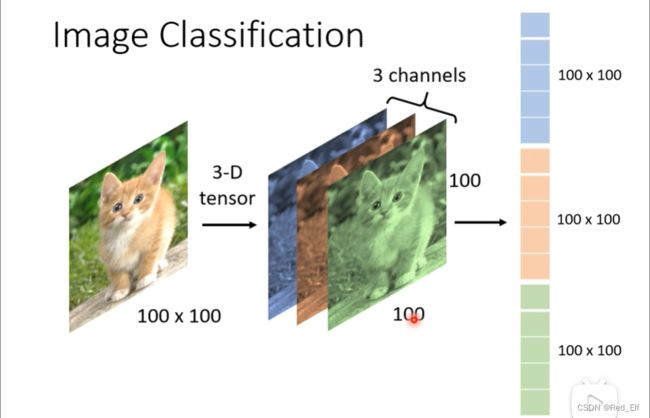
卷积神经网咯(Convolutional Neural Network, CNN),影像用的比较广泛。
以影像分类为例
将图片输入进网络,需要把它变成一维向量:
好,这个一维向量就是网络的输入层,那看一下参数的数量级,真的非常大,参数越多当然可以增加模型的弹性和能力,但是也容易过拟合。
那这样参数太多肯定是不行的,所以我们要简化!
-
简化1:接受域receptive field
我们先想一想自己是怎么进行图片分类的。
给你一张鸟的图片,你是怎么判断它是一只鸟呢?是不是你看到它有喙,有翅膀,有爪子等等,来判断。其实每一个神经元不需要整张图片的信息,只需要一小部分的输入就足以侦测某些特别关键的部分。
好,那怎么拿到这“一部分”呢,这就涉及到Receptive field(接受域,感受野)
对于接受域的选择
- 可以是不同地方,可以重合,可以相同
- 大小可以不同
- 可以只有某些个通道
- 可以不是正方形,而是其他形状
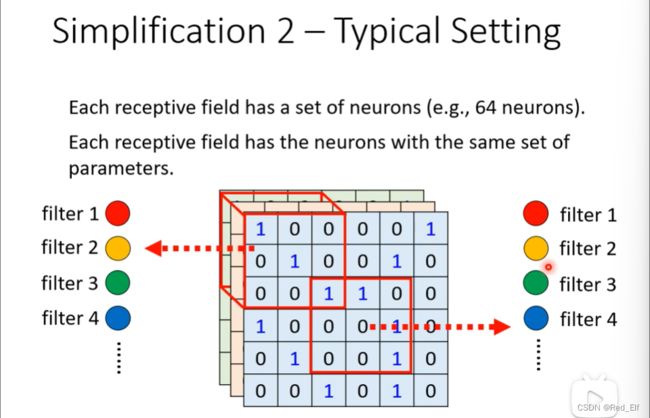
常见的receptive field 会设置成3*3的kernel size,一个接受域都会有好多个神经元负责的,比如64、128。
kernel size:核
stride: 步长
overlap:重叠部分
padding:要补全的地方
这是比较常见的接受域的设置,对整张图片都进行上面的接受域划分。
-
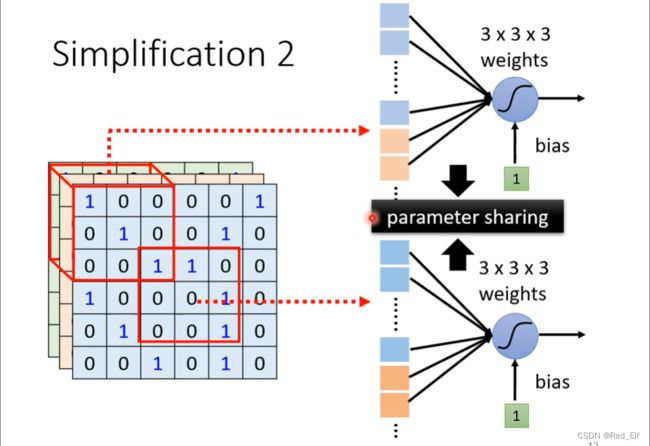
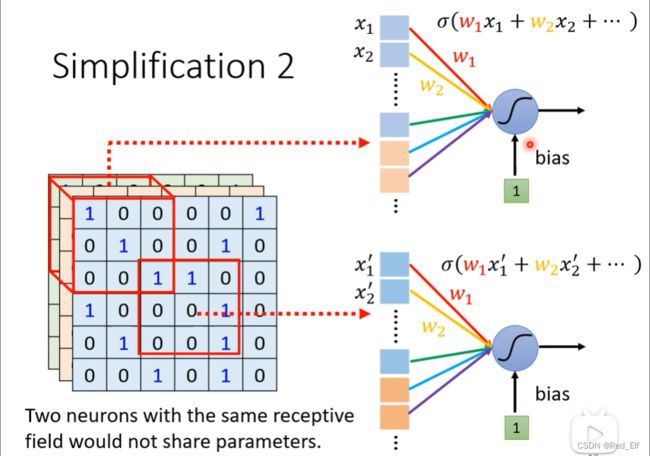
简化2:共享参数parameter sharing
引入一下:你看这两张鸟,是不是都有喙这个部分,而且长得也差不多,但是是不同区域的,分别对应着各自的神经元。那既然是相同的图案,为何不将相对应的神经元的**参数共享(parameter sharing)**呢
之前不是说一个接受域有一组神经元嘛,那每组怎么参数共享呢,相同的**filter(滤波器)**之间是共享的
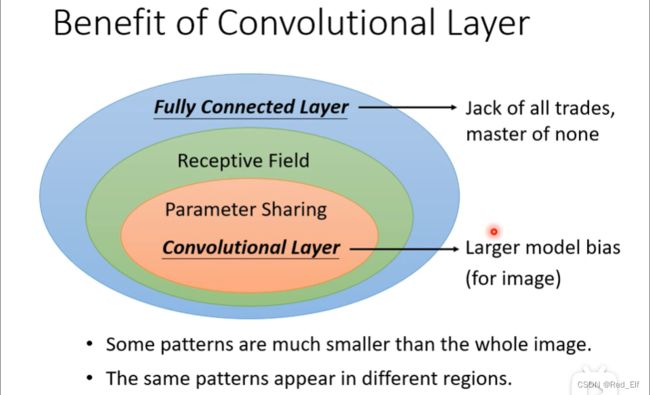
好!经过这几步的简化,我们成功的将全连接层转化为了卷积层(convolutional layer)
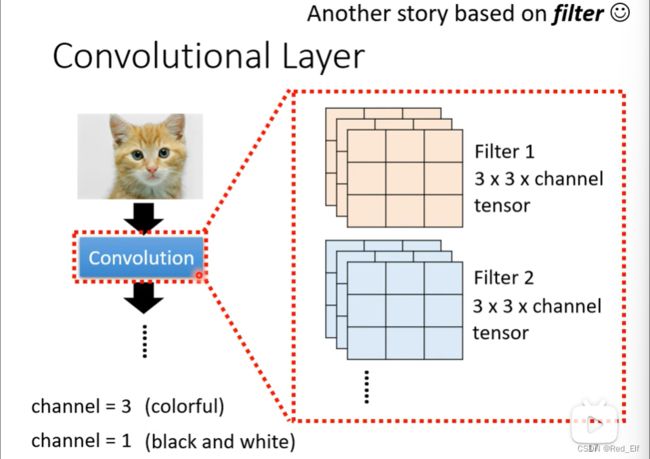
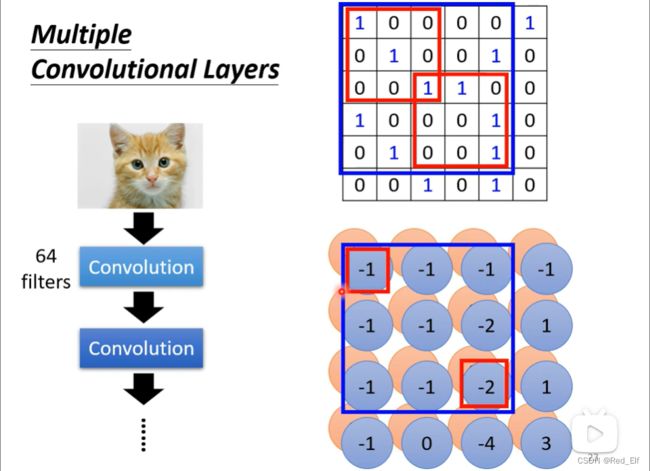
感觉有点模棱两可对吧,下一个例子保你说nb,因为我相信你之前有了解过卷积的计算。一个卷积层里面有一排的filter,我们需要对输出图片进行一系列的与卷积核的计算。
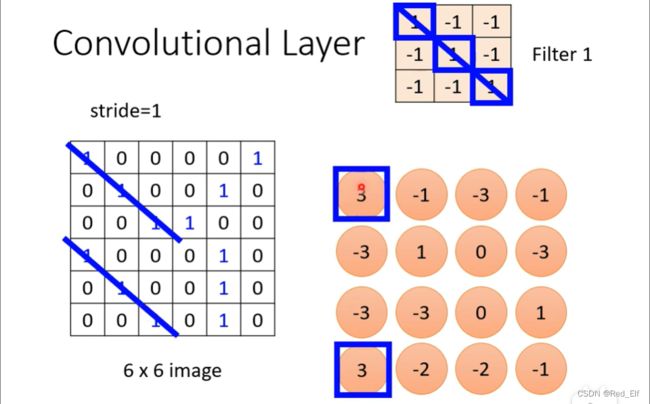
那我们假设channel是1,kernel也已经知道了(这个其实就是参数,需要训练的),比较方便。先进行filter1的计算,怎么计算的都会吧,就是对应值相乘然后加在一起(不会的呢,你可去查CNN,有很经典的动图,看一遍就会了)
这个图里面也表现了filter是如何侦察输入图像的信息的。接下来是filter2
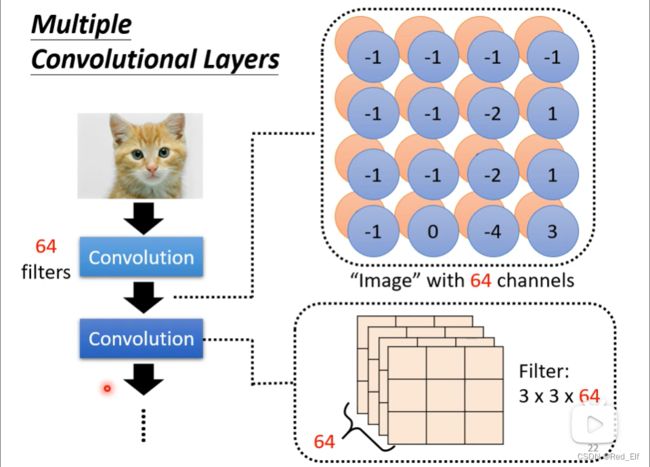
以此类推,看你有多少filter,就有多少层啦。把这些层看成一个整体又名Feature map(特征图谱)
那假设还有一层卷积层,输入就是那个feature map,其实就可以把它看成一个图片,只不过他的通道是很多个的,假设是64个。那这一层的filter的channel数就得设为64了
有个问题,一般filter会设置成3*3的大小,会不会让network的视野很小,不会关注到大范围的图案?其实不会,因为你进行了好几层的学习,深度越深,关注覆盖的范围就越大
很好,之前我们提到过接受域和参数共享,接受域这点相信已经理解了,那参数共享再卷积层中是怎么体现的呢?其实就是filter扫过整张图片的操作,当然,需要设置步长什么的参数值了啦。这个操作其实就叫卷积(convolution)了(是不是连起来了!nb!!!)
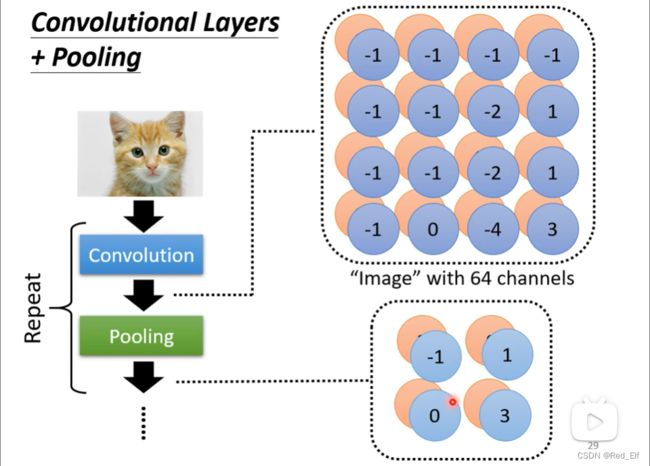
还没完,再补充一个比较常用的东西:pooling(池化)
池化只是一个图片操作而已,没有要学任何东西。
pooling有很多种类,这里讲max pooling
使用pooling的最主要的理由就是为了减少运算量,所以基本上都是卷积层之后跟着池化操作,但是如果计算资源足够的话,也可以舍弃掉这一步骤。但是有缺点,池化操作回损失一些个细节,太精细的特征可能就无法提取到了。
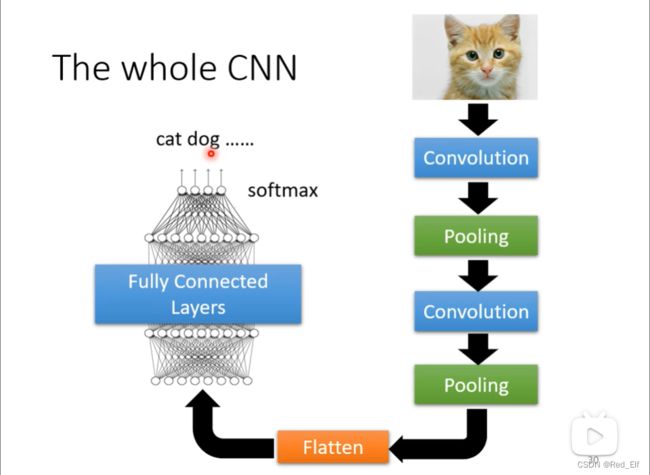
下面的图片是比较常见的CNN结构,经过几次卷积还有pooling操作之后,用flatten把矩阵的东西拉直,然后送进几个固定的全连接层然后再进行softmax操作什么的,最后输出你想要的输出值。
好!卷积大概就是这样!理解起来还蛮容易的叭。
3.2 Spatial Transformer Layer
这节不太理解,大意是说怎么进行输入图片的感兴趣区域的稳定框选,用到了transformer。
这节打算看看相关transformer的论文之后再写笔记叭。
4 自注意力机制(Self-attention)
- 传送门:
- 自注意力机制(Self-attention)(上)
- 自注意力机制(Self-attention)(下)
4.1 引入
之前我们举的例子都是输入一个东西,那如果输入一串东西(sequence)呢?比如一句话、一段语音、一个图(数据结构的图)等等,那相应的输出有哪些形式呢,比如多少个输入就有多少个输出、多入一出还有不知道输出什么让网络自己去判断。
那我们先看第一种情况。
这里又来了一个新词:Sequence Labeling,其实就是把这个Sequence中的每一个向量都给它一个label。
按照之前的思维,接下来就是把每个向量输入网络中,然后输出相应的值,对不对?但是你想一下,加入这个Sequence是个句子,这里面每个词对应一个向量,那向量和向量之间是不是存在这一定的关系,说人话就是上下文语义啊,那怎么做到结合上下文信息呢,看图说话。
我可以让相邻的向量参与到网络中,或者更大一点,那就设置一个window,让window长度的向量作为输入。但是有个问题,这种方法还是有点局限,假如我想获得的是整个句子范围的信息呢,你是不是认为window设置成整个句子的长度不就好了?但是句子的长度是不固定,所以window的长度不能是定值了,而且window越长,网络所需要的参数就越多。
有没有更好的方法呢?所以自适应Self-attention这个概念就被提出来了。
4.2 self-attention
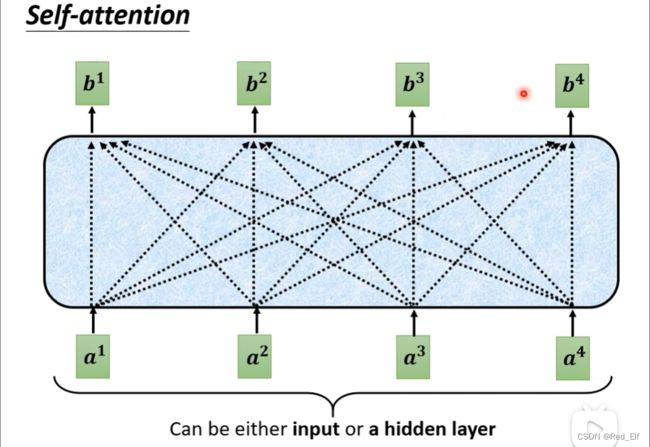
先给出大致的框架,就是说输入几个vector就输出几个vector,输出的vector是考虑整个sequence之后的结果,也就是具有上下文语义的输出向量。而且可以不止一层,就像cnn一样可以叠加很多层。这里FC是指fully-connected network。怎么理解这个过程就是self-attention处理整个sequence的信息,FC专注于处理某一个位置的信息,然后交替使用。
之后会提到最近很火的transformer(5 Transformer),它的主要结构就是self-attention。
好!那里面具体是怎样实现的呢?
输入是一个序列,输出的每一个向量都是输入向量相互学习过的
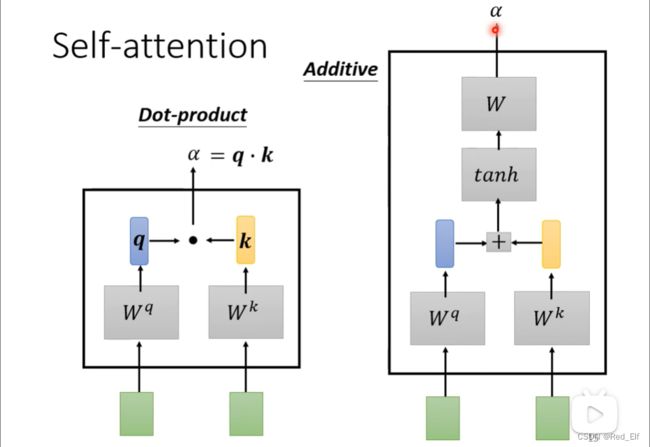
所以下一步我们要解决输入向量之间的关联性( α \alpha α)怎么求,也就是其他哪个向量跟这个向量的关系最紧密或者是同一个level的。以下有几种求法,大部分采用的是左边的求法,之后举例子也是这个方法。
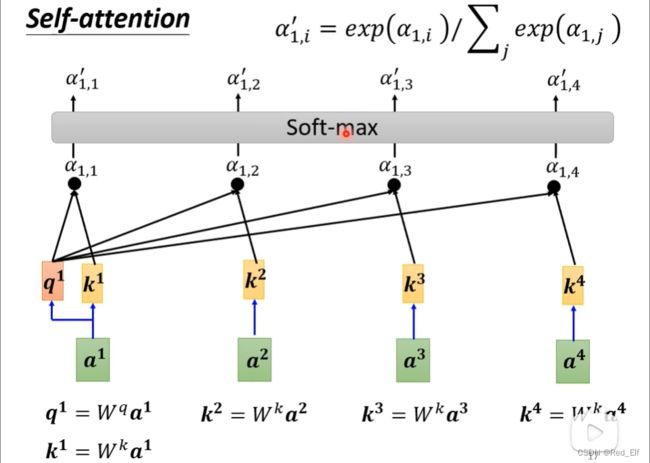
接下来以 a 1 a_1 a1为例,捋一下计算过程和代表的含义:
从下往上一行一行看哈, q 1 , k 1 , . . . q^1,k^1,... q1,k1,...就是上面求 α \alpha α的需要的参数, a 1 a_1 a1跟 a 2 , a 3 , a 4 a_2,a_3,a_4 a2,a3,a4分别计算关联性,即 α 1 , 1 , α 1 , 2 , α 1 , 3 , α 1 , 4 \alpha_{1,1},\alpha_{1,2},\alpha_{1,3},\alpha_{1,4} α1,1,α1,2,α1,3,α1,4然后soft-max一下得出带撇的那一行,也就是归一化了一下。这里的含义就是, a 2 , a 3 , a 4 a_2,a_3,a_4 a2,a3,a4中哪些向量与 a 1 a_1 a1是最有关系的。当然关系越大attention得分 α \alpha α就越大啦
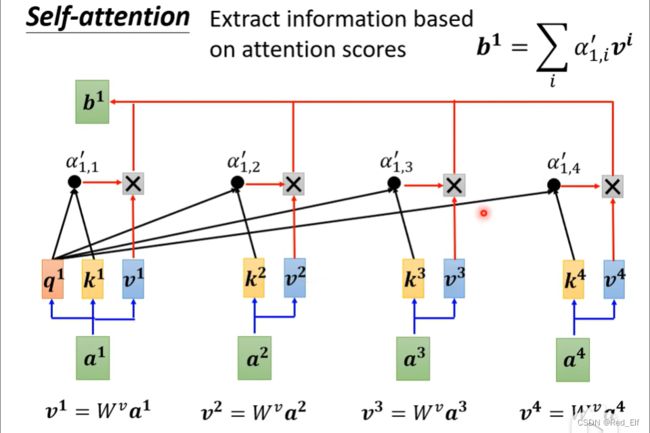
接下来就是要求出关系背后重要的信息了。
从下往上。多了一个 v v v对不对,代表就是 a a a向量中的信息了。然后让 v v v乘上attention值 α ′ \alpha' α′,然后四个加起来得到最终的 b 1 b^1 b1。这里如果一个向量的 α ′ \alpha' α′值越大,也就是与 a 1 a_1 a1关系最紧密,那么得到的 b 1 b^1 b1就越接近这个向量的 v v v,换句话说 v v v在 b b b中占的比重就越大。
好!那 b 2 , b 3 , b 4 b^2,b^3,b^4 b2,b3,b4是不是也就会求了呢,这就是self-attention的输出了哈。
这里注意, b b b的求解不是按顺序产生的,是同时的。那如果要求有位置需求的话,那就需要Positional Encoding了。怎么操作呢?
首先为每一个位置设定一个向量,叫positional vector,设为 e i e^i ei. 然后把 e i e^i ei和 a i a^i ai相加就好了,也就是输入向量带了位置信息参与了attention的计算
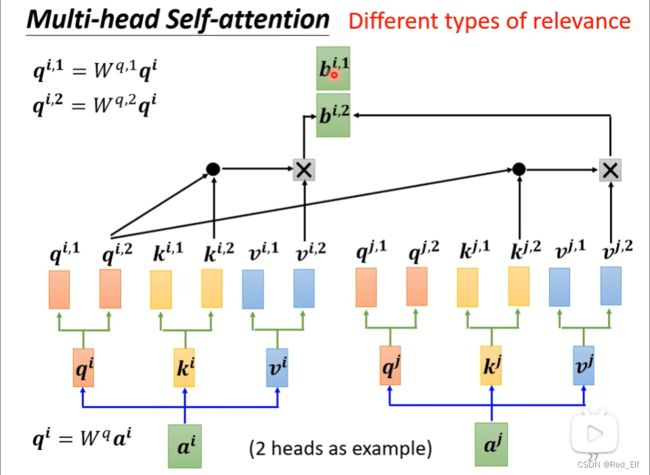
4.3 Multi-head Self-attention
最近看论文也有看到Muti-head Self-attention,来看视频学一下。
首先head的数量是超参数,需要调参侠上线。
那这个head是什么意思呢,就是不同的相关性,在不同方面每个向量信息的关联性也不一样,比如公主和皇后,两个都是女性,所以性别关联非常强,但是两者的地位是不一样的,那这方面的关系就不那么强。
具体实现的话,以head = 2为例,看图
1和2是分开算的,1算1,2算2,最后得到 b i , 1 , b i , 2 b^{i,1},b^{i,2} bi,1,bi,2
然后再transform以下得到 b i b^i bi送到下一层去
5 Transformer
我来提醒你回看[2.5 批次标准化(Batch Normalization)]
接下来就是最近很火的变形金刚Transformer了。
- 传送门:
- Transformer(上)
- Transformer(下)
直接进入正题:
这里补充一下encoder-decoder的相关概念,老师没有讲这个结构的理念,所以在此百度学习
-
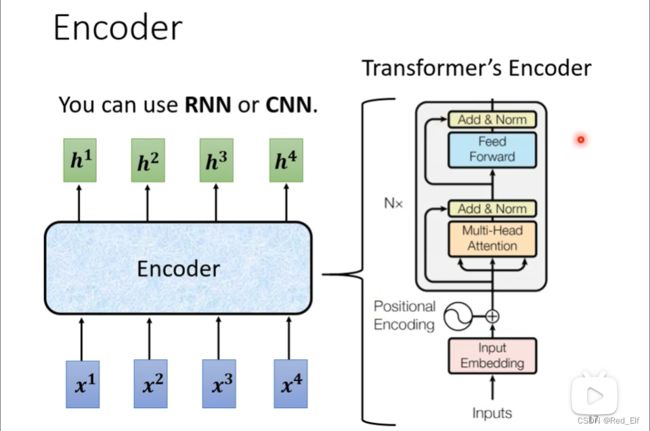
Encoder部分
实际就是输入一排向量,输出一排向量。右边是完整的流程图
看不懂?没关系。换个图看。encoder里面分成很多得block,每个block都是输入一排向量输出一排向量,内部结构有好几层,就是右面大括号里的东东,self-attention一层,FC一层。
但是其实transformer的block内部要比这个复杂一点
- residual:在每一层的输出到输入的时候做一个residual的结构,说人话就是这一层的输出加上这一层的输入,然后norm计算后再作为下一层输入去计算。
- norm:residual之后要Layer Norm,然后再传到下一层。这里的归一化是指向量内部的归一化,跟之前是有区别的,注意一下。
好,简单的图看完,我们回到论文中给出的原版流程图,是不是大致可以看懂了,我们再唠叨一遍。
- 输入一排向量,这里多了一个Positional Encoding,这个之前讲过,是增加了位置信息
- 经过Multi-Head Attention,获取全局信息,经过residual和Layer Norm之后,输出一排向量
- 在经过FC的feed forward network,然后再经过residual和Layer Norm之后,输出一排向量
- 上面两个步骤重复N遍,最后输出一排向量
-
Decoder部分
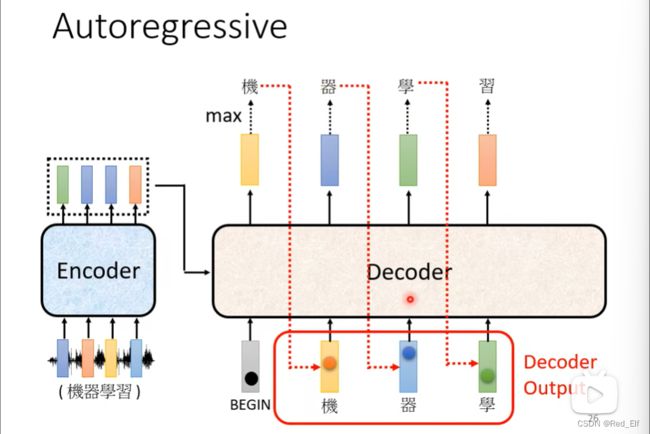
我们先大体了解一下decoder是怎么输入输出的,这对后续内部理解比较重要。
中间Encoder怎么到Decoder后面再说,我们先学习Decoder的结构
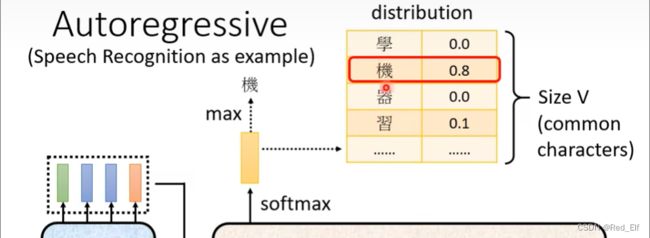
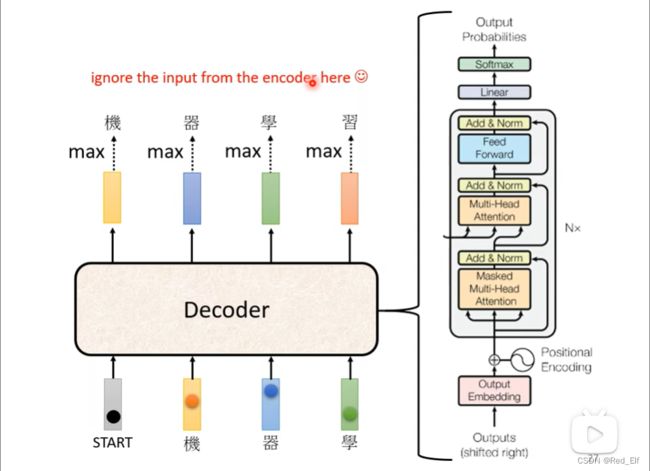
图的右边Decoder模块,从下往上,从左往右看。一开始有个BEGIN模块,这个向量代表一个特殊的符号(没听懂是什么意思,后面理解之后回来补充)。输入这个向量之后,decoder输出一个向量,假如是这样的
然后,把黄色向量作为输入,得到蓝色向量,再把蓝色向量作为输入在输出绿色向量酱紫。所以注意输出会当成下次的输入,所以输入一个一个进行输入的,记住!
好!接下来我们看一下decoder内部是什么样子,放图!!!
hin复杂?没关系!我们对比一下,其实也还好对吧,除了decoder中间加了一层,其他是不是和encoder是差不多的
这里注意一下Multi-Head Attention部分有个Masked,这个是什么意思捏。原本情况self-attention的每一个输出向量都是考虑所有的输入的出来的嘛,但是masked是让每一个输出不能考虑它对应输入后面的输入值,只能考虑对应输入以及它之前的输入。怎么理解?就是只能看到已知序列的内容
为什么要这么做,理由是什么捏?decoder的输入是依次产生的,这和encoder的输入是不同,它是同时输入。所以decoder是不会知道当前输入的后续输入情况的,这一点我们开始的时候强调过(忘记的,回去ε=( o`ω′)ノ)
好!decoder部分特殊的部分就完事了,中间的那一层其实就和encoder与decoder之间的数据传输相关,我们待会就讲(歇会儿)
-
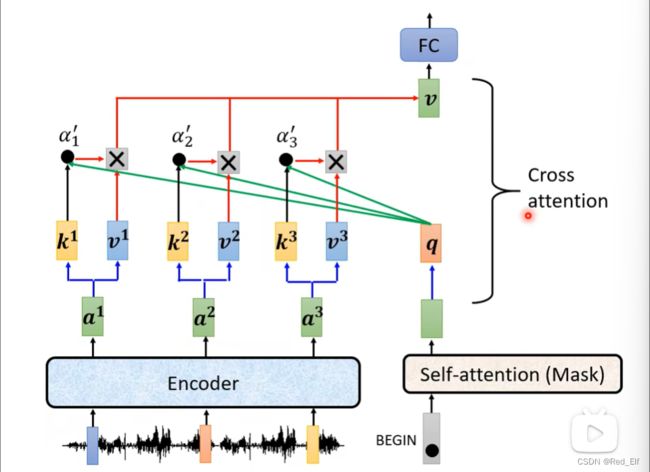
Cross attention:Encoder与Decoder连接部分
其实transformer原图是这样的:
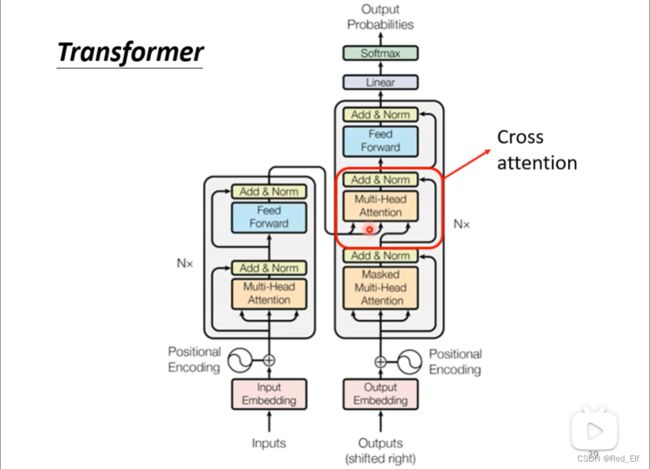
能看清哈,框起来的部分有三个输入,左边两个来自encoder,最右边来自decoder的attention,这个步骤就叫做Cross attention。具体是怎么实现的呢?
decoder这边产生q,然后与encoder的输出做self-attention计算这样。
然后以此类推,就会了吧:
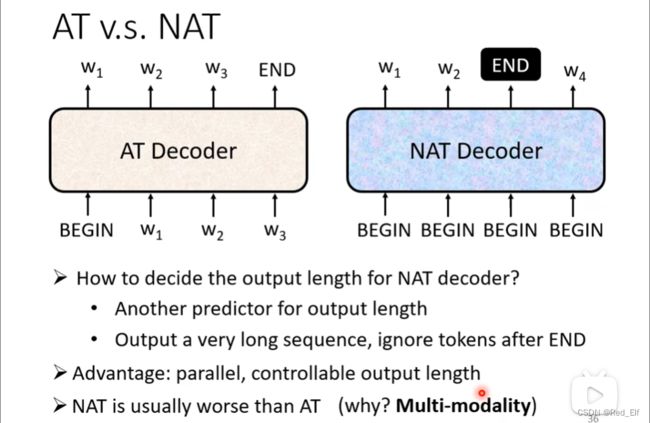
在这,我们补充一个问题。你看你要学习内容然后输出一个序列对不对,那这个序列的长度是多长呢,怎么确定呢?注意并不是encoder输入多少decoder就要输出多少哈,不要被之前的图片误导。
实际上,这个序列是可以无限延长下去,但是这不符合我们想要的结果,假如这个翻译的任务,那翻译出来的句子肯定会结束的。所以还要引入一个结束符END,还记得BEGIN嘛,和这个差不多。
输出的长度不是固定的,长度如何确定,或者说END到底什么时候出现,这里放一张图,自己领悟吧ㄟ( ▔, ▔ )ㄏ
很好!是不是通畅了很多ヾ(≧▽≦*)o
那我们简单看一下训练要怎么训练呢
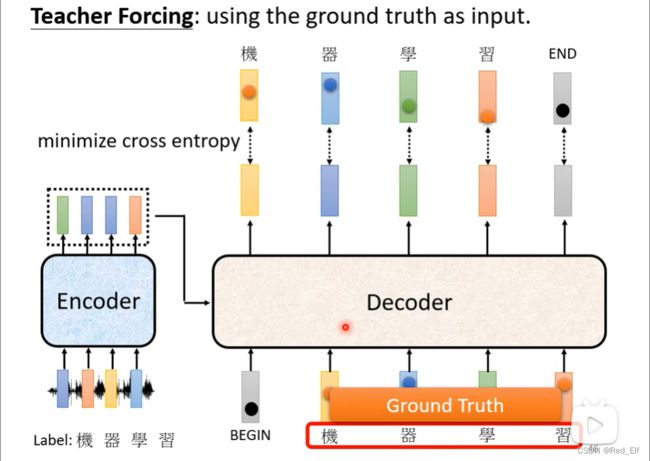
交叉熵作为loss,算distribution和ground truth之间的loss就好了,让他们越接近越好,这里又来了个新名词叫Teacher Forcing,也就是把正确答案当作decoder的输入
好!transformer到这里就差不多啦!