【机器学习作业分享2】极大似然估计方法(MLE)
【机器学习作业分享2】极大似然估计方法(MLE)
- 介绍
- 作业要求
-
- 作业分解
- 作业求解
-
- 任务一求解:运用含噪模型,生成数据,求解结果
- 任务二求解:将任务一得到的数据可视化
- 任务三求解:生成更多组左右数据,绘制 ω ^ \hat{\omega} ω^的二维和三维变化图
介绍
本篇文章是第二次机器学习作业的求解分享。本次作业主要是使用极大似然估计方法对奥运会男子100m数据进行求解。使用的语言为python,编辑器为Jupyter Notebook。数据获取链如下,欢迎大家批评指正,互相交流。
奥运会男子100m数据
作业要求
首先,我们来看一下作业要求。
- 建立两个及两个以上的含噪模型,并给每个模型生成几组数据。
- 运用极大似然方法求解模型
- 将生成的数据集及其对应的拟合曲线(使用一阶直线)可视化
- 进一步,计算出每组模型的数据集训练参数 ω ^ \hat{\omega} ω^的变化情况并将结果可视化
- 根据问题4的可视化结果,观察在不同的先验噪声 σ 2 \sigma^2 σ2下,参数 ω \omega ω训练结果的变化幅度大小,分析其影响
作业分解
我们将作业分解为这四个任务
① 使用两个或者两个以上最大似然含噪模型,每个模型生成3-5组数据,求解出结果来( ω \omega ω, σ \sigma σ)
② 将①的结果可视化,画出数据集和拟合的曲线,用不同的颜色
③ 对于每一个含噪模型(不同的 ω \omega ω, σ \sigma σ),生成更多的数据集(二十个或者更多),分析由生成的数据集反推出 ω ^ \hat{\omega} ω^的情况,绘制出 ω \omega ω变化的三维图和二维等高线图。这个是由数据反推出 ω \omega ω
④ 分析不同的 σ \sigma σ对于cov( ω \omega ω)的影响
作业求解
首先,我们将必要的库导入
# 函数库的导入与设置
import numpy as np
import matplotlib.pyplot as plt
#%matplotlib inline
import pandas as pd
import math
import seaborn as sns
from scipy.linalg import expm,logm
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.axes_grid1.inset_locator import inset_axes
from matplotlib.patches import ConnectionPatch
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
任务一求解:运用含噪模型,生成数据,求解结果
导入数据之后,我们首先对数据进行标准化处理,公式如下:
x s t d = x − x m i n x m a x − x m i n x_{std} = \frac{x-x_{min}}{x_{max}-x_{min}} xstd=xmax−xminx−xmin
# 导入数据并对数据进行标准化
data = np.loadtxt('olympic100m.txt',delimiter=',')
g_x = data[:,0][:,None]
g_t = data[:,1][:,None]
g_x_std = (g_x - g_x.min())/(g_x.max() - g_x.min())
g_t_std = (g_t - g_t.min())/(g_t.max() - g_t.min())
g_N = len(g_x)
#print(x)
首先,我们建立含噪模型,在这里建立了三个含噪模型,分别服从
| μ \mu μ | σ 2 \sigma^2 σ2 |
|---|---|
| 0 | 1 |
| 0 | 0.05 |
| 0 | 0.02 |
的正态分布 N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2)。含噪模型的公式:
t n = ω T x n + ϵ n t_n = \omega^Tx_n + \epsilon_n tn=ωTxn+ϵn
其中 ϵ n \epsilon_n ϵn符合正态分布:
ϵ n ∼ N ( μ , σ 2 ) \epsilon_n\sim N(\mu,\sigma^2) ϵn∼N(μ,σ2)
# 含噪模型的参数
g_mu = [0.0, 0.0, 0.0]
g_sigma_sq = [1, 0.05, 0.02]
根据课本上的公式,最大似然似然估计MLE方法下参数 ω \omega ω和 σ 2 \sigma^2 σ2的估计值分别为:
ω ^ = ( X T X ) − 1 X T t σ 2 ^ = 1 N ( t n o i s e − x T ω ^ ) 2 = 1 N ( t t T − t T X ω ^ ) \begin{aligned} \hat{\omega} =& (X^TX)^{-1}X^Tt \\ \hat{\sigma^2}=&\frac{1}{N}(t_{noise}-x^T\hat{\omega})^2\\ =&\frac{1}{N}(tt^T-t^TX\hat{\omega}) \end{aligned} ω^=σ2^==(XTX)−1XTtN1(tnoise−xTω^)2N1(ttT−tTXω^)
然后,我们先使用标准化后的数据,运用上述公式求解原始数据的 ω \omega ω
# 数据的阶数,这个地方用的是一阶模型
g_X = np.hstack((np.ones_like(g_x_std),g_x_std))
g_w_std = np.dot(np.linalg.inv(np.dot(g_X.T,g_X)),np.dot(g_X.T,g_t_std)) # 最小二乘法求标准omega,由初始数据计算出来的ω
g_sig_sq_std = ( np.dot(g_t.T,g_t) - np.dot(np.dot(g_t.T,g_X),g_w_std) )/g_N
# 展示计算出来的ω
print("ω:",g_w_std)
print("σ^2:",g_sig_sq_std)
之后,对于每一个模型,我们利用随机数生成十组噪声,添加到原有的数据之上
# 生成多组数据
number_data = 10 # 生成数据的组数
number_model = 3# 含噪模型的数量
g_t_noise_all = [] # 存放number组数据
for i in range(number_model): #循环不同的模型
t_noise_model_i = []
for j in range(number_data):# 循环生成多组数据
t_noise_data_j = np.dot(g_X,g_w_std) + np.random.normal(g_mu[i],np.sqrt(g_sigma_sq[i]),(g_t.size,1)) # 生成噪声数据
t_noise_model_i.append(t_noise_data_j)
g_t_noise_all.append(t_noise_model_i)
然后,我们根据上文中给出的公式,分别计算生成的新数据 ω , σ \omega,\sigma ω,σ的估计值 ω ^ , σ ^ \hat{\omega},\hat{\sigma} ω^,σ^。
# 循环计算不同模型、不同数据的ω,μ,σ值
g_w_all = [] #总的ω
#g_mu_all = [] #总的μ
g_sig_sq_all = [] # 总的σ
for i in range(len(g_t_noise_all)):
w_model_i = [] #不同模型的ω
mu_model_i = [] #不同模型的μ
sig_sq_model_i = [] # 不同模型的σ
for j in range(len(g_t_noise_all[0])):
w_data_j = np.dot(np.linalg.inv(np.dot(g_X.T,g_X)),np.dot(g_X.T,g_t_noise_all[i][j]))#ω 这个地方是每一个模型,每一组数据的ω矩阵
sig_sq_data_j = ((g_t_noise_all[i][j]-np.dot(g_X,w_data_j))**2).mean() # 方差
#mu_data_j = np.dot(g_X,w_data_j)
w_model_i.append(w_data_j)
sig_sq_model_i.append(sig_sq_data_j)
#mu_model_i.append(mu_data_j)
g_w_all.append(w_model_i)
g_sig_sq_all.append(sig_sq_model_i)
最终,我们得到了不同模型不同数据的含噪声数据 t n o i s e t_{noise} tnoise, 并计算了每组数据的 ω ^ \hat{\omega} ω^和 σ 2 ^ \hat{\sigma^{2}} σ2^
#结果
for i in range(len(g_t_noise_all)):
print(" ")
for j in range(len(g_t_noise_all[0])):
print("第{model}个模型的第{data}组数据的".format(model=i+1,data=j+1),end="")
print("ω0为:{omega0}".format(omega0=g_w_all[i][j][0]),end=", ")
print("ω1为:{omega1}".format(omega1=g_w_all[i][j][1]),end=", ")
print("方差为:{sig_sq}".format(sig_sq=round(g_sig_sq_all[i][j],2)))
任务二求解:将任务一得到的数据可视化
首先,我们画出原始数据和标准回归直线:
fig, axes = plt.subplots(1, 1, figsize = (10,7))
axes.plot(g_x_std,g_t_std,color="red",marker="o",linestyle=" ",
label="原始数据点")
axes.plot(g_x_std,np.dot(g_X,g_w_std),color="black",marker=" ",linestyle="-",linewidth=3,alpha=0.7,
label="标准回归曲线")
axes.set_ylabel("t_std")
axes.set_xlabel("x_std")
axes.set_title("标准化后原始数据及其回归直线")
axes.legend()
axes.grid()
绘制出来的图片如下所示
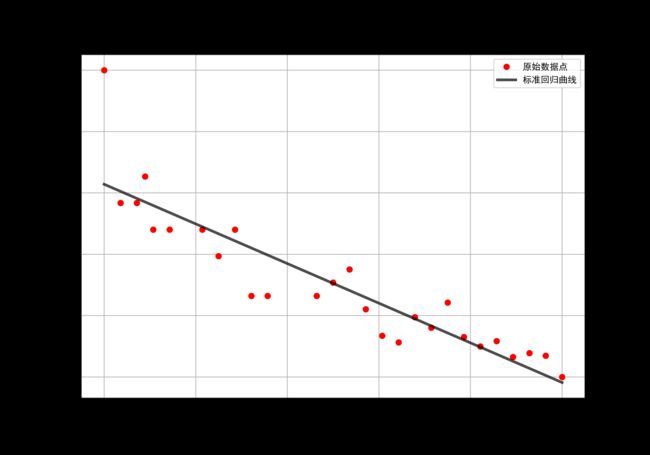
下面,我们将对生成的数据进行可视化。在之前,先选择绘图的颜色。
# 颜色设置
b = plt.colormaps['Accent']( ### 这个地方可以通过colormaps来调整颜色变化
np.linspace(0.15, 0.85, 10))
下面进行可视化,思路为,将生成的数据点和回归的直线,按照模型的不同分别绘制。
cols1 = 2 # 列数
rows1 = 3 # 行数
fig2, axes2 = plt.subplots(rows1,cols1, figsize=(12,12)) # 绘制子图
for i in range(number_model): # 模型遍历
for j in range(2):
if(j == 0 ): # 绘制散点
axes2[i,j].plot(g_x_std,np.dot(g_X,g_w_std),color="black",marker=" ",linestyle="-",linewidth=3,alpha=1,
label="标准拟合曲线")
for k in range(number_data):
axes2[i,j].plot(g_x_std,g_t_noise_all[i][k],color=b[k],marker="o",linestyle=" ",markersize=4,
label="生成的数据点")
else:
axes2[i,j].plot(g_x_std,np.dot(g_X,g_w_std),color="black",marker=" ",linestyle="-",linewidth=3,alpha=1,
label="标准拟合曲线")
for k in range(number_data):
axes2[i,j].plot(g_x_std,np.dot(g_X,g_w_all[i][k]),color="black",marker=" ",linestyle="-",linewidth=3,alpha=0.2,
label="生成数据的拟合曲线")
axes2[i,j].set_title("$\sigma^2=$%s"%g_sigma_sq[i])
axes2[i,j].grid()
绘制出来的图片就像这样:
左半部分的三张子图展示了不同 σ 2 \sigma^2 σ2下的数据离散变化情况。其中黑色的直线为标准数据的回归直线,不同颜色的散点则代表不同组数据。
右边的三张子图展示了不同 σ 2 \sigma^2 σ2下的回归直线情况。其中黑色的直线为标准数据的回归直线,灰色的直线为不同数据的回归直线。
分析上图,不难发现,当 σ 2 \sigma^2 σ2更大时,数据点会变得更加离散,与原始的标准回归曲线的相差会变得更大,回归直线自然也变得杂乱无章
任务三求解:生成更多组左右数据,绘制 ω ^ \hat{\omega} ω^的二维和三维变化图
首先,仍根据任务一建立的模型生成数据,这次,我们生成10,000组数据。
# 生成更多的数据数据
number_data_more = 10000 # 生成数据的组数
number_model = 3# 含噪模型的数量
g_t_noise_all_more = [] # 存放number组数据 1 * 10000
for i in range(number_model): #循环不同的模型
t_noise_model_i = []
for j in range(number_data_more):# 循环生成多组数据
t_noise_data_j = np.dot(g_X,g_w_std) + np.random.normal(g_mu[i],np.sqrt(g_sigma_sq[i]),(g_t.size,1)) # 生成噪声数据
t_noise_model_i.append(t_noise_data_j)
g_t_noise_all_more.append(t_noise_model_i)
然后,计算每一组的 ω ^ \hat{\omega} ω^值:
# 计算每一组数据的ω,σ值
g_w_all_more = [] #总的ω 组数更多的ω
#g_mu_all = [] #总的μ
g_sig_sq_all_more = [] # 总的σ
for i in range(len(g_t_noise_all_more)):
w_model_i = [] #不同模型的ω
#mu_model_i = [] #不同模型的μ
sig_sq_model_i = [] # 不同模型的σ
for j in range(len(g_t_noise_all_more[0])):
w_data_j = np.dot(np.linalg.inv(np.dot(g_X.T,g_X)),np.dot(g_X.T,g_t_noise_all_more[i][j]))#ω 这个地方是每一个模型,每一组数据的ω矩阵
sig_sq_data_j = ((g_t_noise_all_more[i][j]-np.dot(g_X,w_data_j))**2).mean() # 方差
#mu_data_j = np.dot(g_X,w_data_j)
w_model_i.append(w_data_j)
sig_sq_model_i.append(sig_sq_data_j)
#mu_model_i.append(mu_data_j)
g_w_all_more.append(w_model_i)
g_sig_sq_all_more.append(sig_sq_model_i)
#g_mu_all.append(mu_model_i)
#
之后,对数据进行处理,为之后的绘图做准备。这里是将上段代码中计算的 ω ^ \hat{\omega} ω^进行提取。
# 数据处理,提取w0 和w1
g_w0_more = [] # 存储w0
g_w1_more = [] # 存储w1
#logL = [] # 储存似然值
for i in range(len(g_w_all_more)):
w0_more_i = []
w1_more_i = []
for j in range(len(g_w_all_more[i])):
w0_more_i.append(g_w_all_more[i][j][0][0])
w1_more_i.append(g_w_all_more[i][j][1][0])
g_w0_more.append(w0_more_i)
g_w1_more.append(w1_more_i)
最终,对于生成的数据,我们推出了每一组数据的 ω ^ \hat{\omega} ω^值和 σ ^ 2 \hat{\sigma}^2 σ^2值。分别存储在上个 c o d e c e l l codecell codecell的 g _ w _ 0 _ m o r e g\_w\_0\_more g_w_0_more, g _ w _ 1 _ m o r e g\_w\_1\_more g_w_1_more 和 g _ s i g _ s q _ a l l _ m o r e g\_sig\_sq\_all\_more g_sig_sq_all_more 中。
下面分别绘制 ω 0 \omega_0 ω0和 ω 1 \omega_1 ω1的二维和三维关系图来展示其变化情况
首先,将画图所需要的数据存储到一张pandas.DataFrame g _ d a t a g\_data g_data里,便于绘图。
# 将绘图所需要的数据整合成dataframe
g_data = pd.DataFrame(g_w0_more[0]) # DataFrame
g_data.columns = ["w0_1"]
g_data["w1_1"] = pd.DataFrame(g_w1_more[0])
t_a_1 = pd.DataFrame(pd.cut(g_data["w0_1"],10)) # 将w0_1进行分箱
t_b_1 = pd.DataFrame(pd.cut(g_data["w1_1"],10)) # 将w1_1进行分箱
g_data["w0_1_bin"] = t_a_1
g_data["w1_1_bin"] = t_b_1
g_data["w0_2"] = pd.DataFrame(g_w0_more[1])
g_data["w1_2"] = pd.DataFrame(g_w1_more[1])
t_a_2 = pd.DataFrame(pd.cut(g_data["w0_2"],10)) # 将w0_2进行分箱
t_b_2 = pd.DataFrame(pd.cut(g_data["w1_2"],10)) # 将w1_2进行分箱
g_data["w0_2_bin"] = t_a_2
g_data["w1_2_bin"] = t_b_2
g_data["w1_3"] = pd.DataFrame(g_w1_more[2])
g_data["w0_3"] = pd.DataFrame(g_w0_more[2])
t_a_3 = pd.DataFrame(pd.cut(g_data["w0_3"],10)) # 将w0_3进行分箱
t_b_3 = pd.DataFrame(pd.cut(g_data["w1_3"],10)) # 将w1_3进行分箱
g_data["w0_3_bin"] = t_a_3
g_data["w1_3_bin"] = t_b_3
# 每个模型的分箱区间
x_1 = [-0.877, -0.584, -0.293, -0.00271, 0.288, 0.578, 0.869, 1.16, 1.45, 1.741]#, 2.031] # w0分箱后的区间端点
y_1 = [-3.217, -2.666, -2.12, -1.575, -1.029, -0.483, 0.0626, 0.608, 1.154, 1.7]#, 2.245]# w1分箱后的区间端点
x_2 = [0.301, 0.368, 0.435, 0.501, 0.567, 0.634, 0.7, 0.767, 0.833, 0.899]#, 0.966] # w0_2分箱后的区间端点
y_2 = [-1.152, -1.049, -0.947, -0.845, -0.743, -0.641, -0.539, -0.436, -0.334, -0.232]#, -0.13]# w1_2分箱后的区间端点
x_3 = [0.406,0.447,0.489, 0.53, 0.572,0.613,0.655,0.696, 0.738, 0.779]# 0.821] # w0_3分箱后的区间端点
y_3 = [-0.975, -0.911,-0.847, -0.784, -0.72, -0.657, -0.593, -0.53,-0.466, -0.402] #-0.339] w1_3分箱后的区间端点
# 总的分箱区间
x = [x_1,x_2,x_3]
y = [y_1, y_2, y_3]
这样,就生成了储存三个模型的 w 0 w_0 w0和 w 1 w_1 w1的 D a t a F r a m e DataFrame DataFrame,其结构如下:
g_data.head(5)
下面,来绘制三维立体图,首先,通过创建交叉表来统计各组的频数,下面展示了第一个模型 0 _0 w0 和 1 _1 w1 的交叉表
# w0和w1的二维交叉表
t_pb = pd.crosstab(g_data['w0_1_bin'], g_data['w1_1_bin'])
t_pb.head(5)
#统计三个模型每个模型的频数
# w0_1和w1_1的二维交叉表
t_pb_1 = pd.crosstab(g_data['w0_1_bin'], g_data['w1_1_bin'])
z_1 = t_pb_1.values.T
z_1 = z_1.ravel()
# w0_2和w1_2的二维交叉表
t_pb_2 = pd.crosstab(g_data['w0_2_bin'], g_data['w1_2_bin'])
z_2 = t_pb_2.values.T
z_2 = z_2.ravel()
# w0_3和w1_3的二维交叉表
t_pb_3 = pd.crosstab(g_data['w0_3_bin'], g_data['w1_3_bin'])
z_3 = t_pb_3.values.T
z_3 = z_3.ravel()
#三个模型频数的汇总
z = [z_1,z_2,z_3]
之后,我们将数据坐标化处理
# 将x,和y坐标化处理
xx_1, yy_1=np.meshgrid(x[0], y[0])#网格化坐标(w0,w1)
xx_2, yy_2=np.meshgrid(x[1], y[1])#网格化坐标(w0,w1)
xx_3, yy_3=np.meshgrid(x[2], y[2])#网格化坐标(w0,w1)
绘制三维立体图
# 绘图设置
fig11 = plt.figure(figsize=(10,10))
ax11 = fig11.add_subplot(projection = '3d')
# X和Y的个数要相同
X = xx_1.ravel()
Y = yy_1.ravel()
Z = z[0]
# 设置柱子属性
height = np.zeros_like(Z) #
width = depth = 0.3 # 柱子的长和宽
# 绘图
ax11.bar3d(X, Y, height, width, depth, Z, color=b[4], shade=True) # width, depth, height
ax11.set_xlabel('w0_1',fontsize=10)
ax11.set_ylabel('w1_1',fontsize=10)
ax11.set_zlabel('',fontsize=10)
ax11.set_title("$\sigma^2=1$")
#plt.savefig("333.png",dpi = 400)
#####################################################################3
# 绘图设置
fig12 = plt.figure(figsize=(10,10))
ax12 = fig12.add_subplot(projection = '3d')
# X和Y的个数要相同
X = xx_2.ravel()
Y = yy_2.ravel()
Z = z[1]
# 设置柱子属性
height = np.zeros_like(Z) #
width = depth = 0.3 # 柱子的长和宽
# 绘图
ax12.bar3d(X, Y, height, width, depth, Z, color=b[4], shade=True) # width, depth, height
ax12.set_xlabel('w0_2',fontsize=10)
ax12.set_ylabel('w1_2',fontsize=10)
ax12.set_zlabel('',fontsize=10)
ax12.set_title("$\sigma^2=0.05$")
#plt.savefig("444.png",dpi = 400)
##################################################################################################
# 绘图设置
fig13 = plt.figure(figsize=(10,10))
ax13 = fig13.add_subplot(projection = '3d')
# X和Y的个数要相同
X = xx_3.ravel()
Y = yy_3.ravel()
Z = z[2]
# 设置柱子属性
height = np.zeros_like(Z) #
width = depth = 0.3 # 柱子的长和宽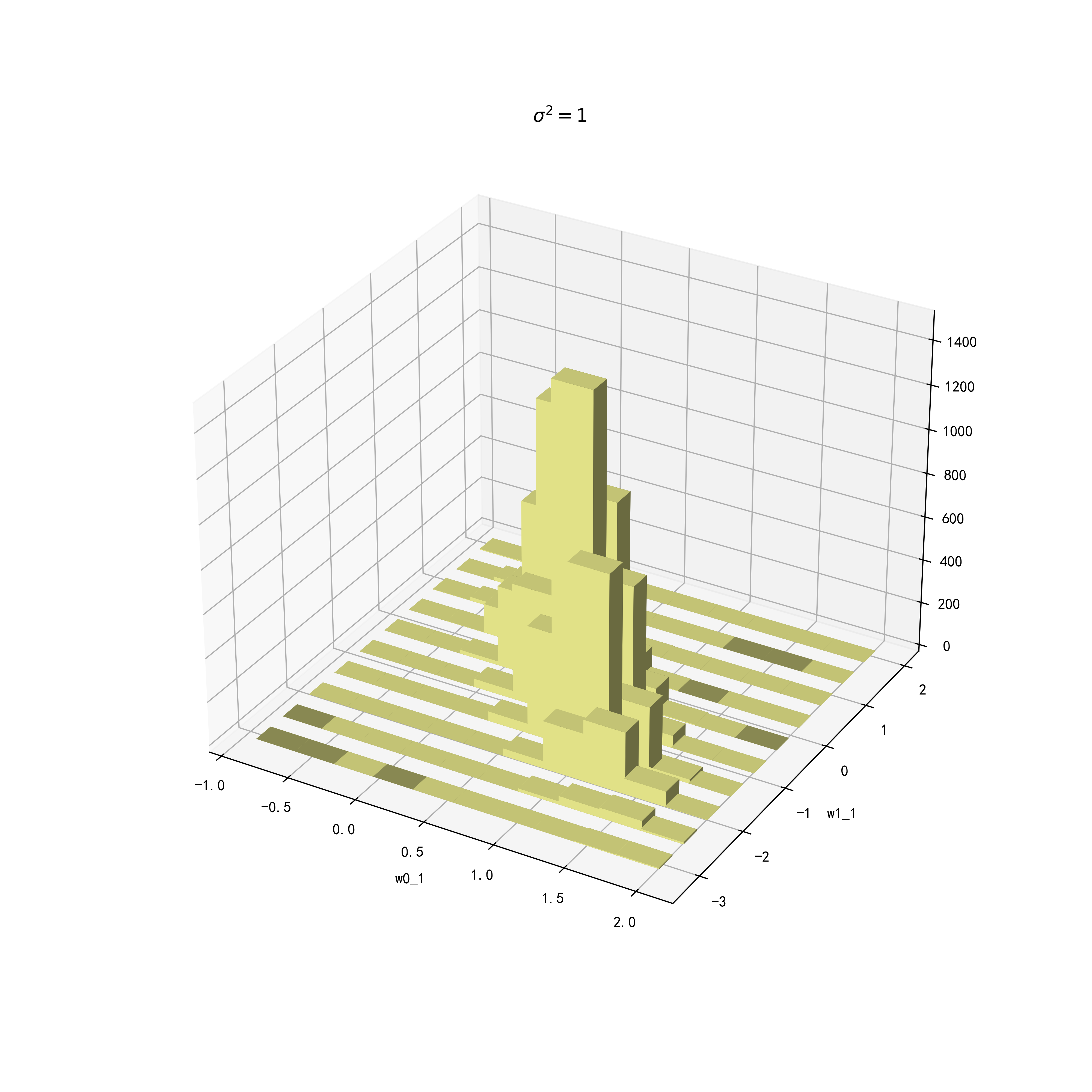
# 绘图
ax13.bar3d(X, Y, height, width, depth, Z, color=b[4], shade=True) # width, depth, height
ax13.set_xlabel('w0_2',fontsize=10)
ax13.set_ylabel('w1_2',fontsize=10)
ax13.set_zlabel('',fontsize=10)
ax13.set_title("$\sigma^2=0.02$")
#plt.savefig("555.png",dpi = 400)
效果如下:


从上面三幅图可以看到,无论是哪个模型, w 0 w_0 w0和 w 1 w_1 w1呈现出负相关的关系。对于 σ 2 \sigma^2 σ2大的模型,其数据分布范围较大,反之则较小。
下面绘制二维曲线图(下面两个绘制图片的code运行时间较长)
fig, axes22 = plt.subplots(1,3,figsize=(30,10))
# 绘制联合分布图
g1 = sns.jointplot(x=g_data['w1_1'], y=g_data['w0_1'], kind="kde",ax = axes22[0])
g2 = sns.jointplot(x=g_data['w1_2'], y=g_data['w0_2'], kind="kde",ax = axes22[1])
g3 = sns.jointplot(x=g_data['w1_3'], y=g_data['w0_3'], kind="kde",ax = axes22[2])
#去掉边缘图
g1.ax_marg_x.remove()
g1.ax_marg_y.remove()
g2.ax_marg_x.remove()
g2.ax_marg_y.remove()
g3.ax_marg_x.remove()
g3.ax_marg_y.remove()
# 设置标题
axes22[0].set_title("$\sigma^2=1$")
axes22[0].set_xlim(-2.5,1.5)
axes22[0].set_ylim(-1,2)
axes22[1].set_title("$\sigma^2=0.05$")
axes22[1].set_xlim(-2.5,1.5)
axes22[1].set_ylim(-1,2)
axes22[2].set_title("$\sigma^2=0.02$")
axes22[2].set_xlim(-2.5,1.5)
axes22[2].set_ylim(-1,2)
fig
效果如下:

上面三张二维图较三维图将 w 0 w_0 w0和 w 1 w_1 w1的关系展示的更为直观,从上面的密度图可以看到,二者的关系与模型参数取值无关,是一个负相关关系。而随着 σ \sigma σ的增大, ω ^ \hat{\omega} ω^的协方差也变大,整体看起来更为离散
下面采用 s e a b o r n seaborn seaborn库中的 P a i r G r i d PairGrid PairGrid函数来展示一种更直观的可视化方法。
下图分别用密度图和散点图展示了 g _ d a t a g\_data g_data中各个变量之间的关系
g = sns.PairGrid(g_data)
g.map_upper(sns.scatterplot)
g.map_lower(sns.kdeplot)
g.map_diag(sns.kdeplot)
效果如下: