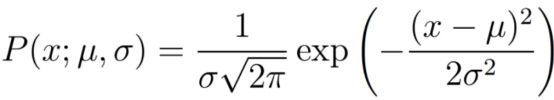概率论之概念解析:极大似然估计
原文地址:https://cloud.tencent.com/developer/article/1093491
【导读】本文是数据科学家Jonny Brooks-Bartlett概率论基础概念系列博客中的“极大似然估计”一章,主要讲解了极大似然估计的若干概念。分别介绍了参数、直观理解极大似然估计、极大似然估计计算方法、极大似然估计与最小二乘法的区别、极大似然与极大概率的区别,作者层层递进、由浅及深地带我们揭开极大似然估计的神秘面纱,如果你对其概念和算法仍然有所迷惑,那么这篇文章或将给你带来更深的理解。专知内容组编辑整理。Probability concepts explained: Maximum likelihood estimation
▌简介
这次我将介绍参数估计的极大似然法,并且使用一个简单的例子来解释这一方法。某些内容需要一些基础的概率概念,例如联合概率和事件独立的定义。我已经写了有关这些预备知识的博客,https://medium.com/@jonnybrooks04/probability-concepts-explained-introduction-a7c0316de465,如果你觉得需要补习的话可以先阅读一下。
▌什么是参数?
通常在机器学习中,我们使用一个模型来描述我们看到的数据。例如,我可能用一个随机森林模型来分析用户是否可能取消服务的订阅(被称作客户流失模型churn modelling),或者使用一个线性模型,根据公司在广告上的花费来预测他们的收益(这将是线性回归的一个例子)。每个模型都有自己的一组参数,最终决定了模型的质量。
对于线性模型,可以写成
。在这个例子中,x可以代表广告花费,y可以代表产生的收益,m和c是模型的参数,这些参数不同的取值会得到不同的线(看下面这幅图)。
所以,参数决定了模型的形状。只有当我们选择了一个具体的参数值后,才得到了一个描述给定现象的实例化模型。
▌极大似然估计的直观解释
极大似然估计是估计模型参数的一种方法。通过最大化模型得到最终的参数值。
上面的定义看起来有些晦涩,所以我们用一个例子来辅助理解。
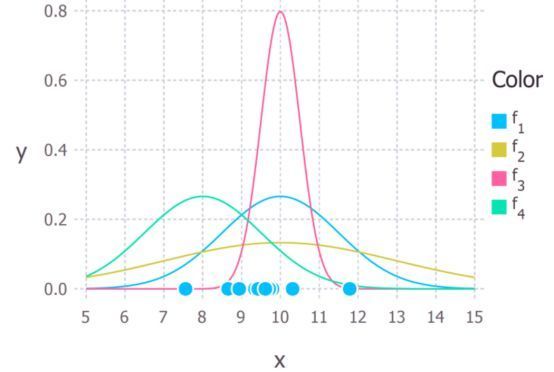
假设我们有10个观测数据点,例如,每个数据点可以表示时间的长度,代表某个学生解答某个具体的考试题所消耗的时间(ms)。这10个数据点可以用下图来表示:
我们首先必须明确采用什么模型能很好地描述这些数据,这是非常重要的。起码我们得对使用什么模型有一个好想法,这一想法经常来源于某些领域的专业知识,不过我们不在这里讨论。
对于这些数据,我们假设可以用一个高斯(正态)分布来描述。看看上面这个图感觉高斯分布似乎很合理,因为10个点中很多都聚集在中间,少部分点散布在左右(对10个数据点做这种草率的决定是不推荐的,不过这些数据是我生成的,所以我们就暂且按照高斯分布来讲解)。
高斯分布具有两个参数:均值和标准差σ。不同的参数取值会导致不同的曲线。我们想知道什么曲线最有可能生成我们看到的这些数据点(看下面的图)?极大似然估计是寻找最匹配曲线的均值和方差的一个方法。
这10个数据点和可能服从的高斯分布,f1均值为10,方差为2.25,也可以标记为
和
,极大似然方法的目标是找到一组参数值,最大化生成这些数据点的概率。
我们生成数据点的真实分布为
,就是上图的蓝色曲线。
▌计算极大似然估计
现在我们对什么是极大似然估计有了直观的理解,然后继续学习怎样计算这些参数值。我们得到的这些值被称为极大似然估计(MLE)。
我们将再一次用一个例子进行演示。假设这次我们有三个数据点,并且可以用高斯分布来进行描述。这些点是9,9.5和11,我们该怎么计算高斯分布的均值和方差σ这些参数值的极大似然估计呢?
我们想要计算的是看到所有这些数据的总概率,例如所有观测到的数据点的联合分布。为了做到这一点,我们需要计算条件概率,但这一点可能很难做到。因此我们在这里做了第一个假设:这个假设是每个生成的数据独立,这一假设让数学计算大大简化。如果这些事件(i.e.生成这些数据的过程)是独立的,此时观测到所有这些数据的总概率等于独立观测到每个数据点的概率之积(i.e.边际分布的乘积)。
观测到用高斯分布生成的某个单独数据点x的边际概率,可以由下式得到:
中间的分号是用来强调标记后面的是概率分布的参数,从而不会与条件分布混淆(条件分布通常中间是条竖线
)
观测到这三个数据点的总概率(联合概率)为
我们现在只需要弄清楚什么均值和方差σ的值可以得到给定表达式的最大值。
如果你在数学课上学过微积分,那么你很可能意识到有一种方法可以帮助我们得到函数的最大值点(或最小值点)。这种方法叫微分。我们现在要做的只是得到函数的导数,让导函数为0然后解方程,求解感兴趣的参数。现在我们就得到了参数的MLE值。假设读者都知道怎么使用微分求解函数,所以我只是简要讲解这些步骤,如果你想要更详细的解释可以在评论区告诉我。
▌对数似然
上面的总概率表达式求导起来很麻烦,所以总是对概率公式进行求对数,以简化求解,因为自然对数是单调递增函数。这意味着当x的值增大y的值也会增大(见下图)。这很重要,因为这保证了概率函数的对数的最大值点和原始概率函数的最大值点是同一个点。因此我们可以使用简单的对数似然而不是原始似然。
函数的单调性,左边是y=x,右边是自然对数y=ln(x),这些函数都是单调的,因为随着x增加y都在增大。
一个非单调函数的例子,当x从左到右,y的值先增大后减小再增大
对原始表达式取对数,得到:
使用对数计算法则,这个表达式可以简化为:
这个函数可以求导得到最大值,在这个例子中我们将得到均值的MLE,对均值求偏导得到:
令左边为0,重排表达式得到
于是我们就得到了的极大似然估计。我们可以对σ做同样的操作,但是我会把这个留作热心读者的作业。
▌结束语
- 极大似然估计总是可以得到精确的解吗?
答案很简单,不是!在现实世界的场景中,对数似然函数的导数很可能是难以分析的(例如函数的导数不能求解)。因此迭代方法如EM算法(Expectation-Maximization)用来求解模型的参数。总的想法还是一样的。
- 为什么是极大似然而不是极大概率?
其实,大部分人想要让概率和似然可以互相替换,但是统计学家和概率理论家硬把两者区分开来,区分的理由是。
其实这两个表达也是等价的!所以这意味着什么呢?首先,
表示使用均值为和方差为σ的模型观测到这些数据的概率。我们可以把这个概念推广到任何模型上。另一方面,
意味着:给定我们观测到的值,参数和σ的得到特定的似然。
这个等式意味着,给定参数得到观测数据的概率等价于给定观测数据得到参数的似然。尽管这两个式子是等价的,但是似然和概率从基础上来讲是不同的问题——一个问的是数据,另一个问的是参数值。这也是为什么我们的方法叫极大似然而不是极大概率。
- 什么时候最小二乘法和极大似然法是一样的?
最小二乘法是机器学习中另一个估计模型的参数值的常用方法。和上面的例子一样,当模型假设是高斯的,极大似然估计和最小二乘法等价。数学求导过程可以看这个幻灯片:
https://web.archive.org/web/20111202153913/http://www.cs.cmu.edu/~epxing/Class/10701/recitation/recitation3.pdf
我们可以通过理解两个方法的目标来解释他们。对最小二乘估计,我们想要找到一条线,来最小化全部数据点和回归线的平方距离(可以看下面的图)。对于极大似然估计,我们想要最大化数据的总概率。当假设为高斯分布时,数据点离均值近的时候得到最大概率。由于高斯分布是对称的,这等价于最小化数据点和均值之间的距离。
如果你对本文有任何不清楚的地方,或者我上面的内容有什么错误,可以留下你的评论。在下一个帖子我准备讲述贝叶斯推断以及它是怎样被用来参数估计的。
感谢您的阅读。
原文链接:
https://towardsdatascience.com/probability-concepts-explained-maximum-likelihood-estimation-c7b4342fdbb1
Jonny Brooks-Bartlett是知名的数据科学家、演说家;数学家,主页:
https://towardsdatascience.com/@jonnybrooks04?source=post_header_lockup