TensorFlow2 | RNN—时间序列预测—几个简单代码例子

代码整理自 《Hands On Machine Learning with sklearn,Keras and TensorFlow》Chapter 15: Processing Sequences Using RNNs and CNNs。

1.生成模拟数据

import numpy as np
import matplotlib.pyplot as plt
from tensorflow import keras
#### 模拟数据生成函数：多个正弦波+随机噪音
def generate_time_series(batch_size, n_steps,seed=10):
    np.random.seed(seed)
    freq1, freq2, offsets1, offsets2 = np.random.rand(4, batch_size, 1)
    time = np.linspace(0, 1, n_steps)
    series = 0.5 * np.sin((time - offsets1) * (freq1 * 10 + 10)) # wave 1
    series += 0.2 * np.sin((time - offsets2) * (freq2 * 20 + 20)) # + wave 2
    series += 0.1 * (np.random.rand(batch_size, n_steps) - 0.5) # + noise
    return series[..., np.newaxis].astype(np.float32)
#### 生成模拟时间序列以及训练集和测试集
n_steps = 50
series = generate_time_series(10000, n_steps + 1)
X_train, Y_train = series[:7000, :n_steps], series[:7000, -1]
X_valid, Y_valid = series[7000:9000, :n_steps], series[7000:9000, -1]
X_test, Y_test = series[9000:, :n_steps], series[9000:, -1]

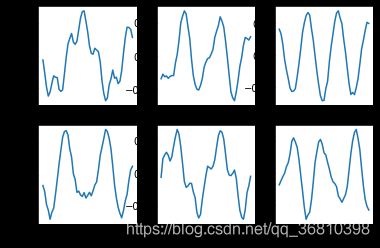
模拟数据大致模样如下图所示：

2.朴素预测方法作为基准预测方法

预测结果约为 mse=0.019979032。

####朴素预测方法（naive forecast）作为预测效果比较
Y_pred = X_valid[:, -1]
np.mean(keras.losses.mean_squared_error(Y_valid, Y_pred))

3.预测未来的1个值

3.1 TensorFlow线性回归预测

预测结果约为 mse=0.003～0.004，比基准预测效果好得多。

#### linear regression
model = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[50, 1]),
    keras.layers.Dense(1)
])
model.compile(loss=keras.losses.mean_squared_error,
              optimizer=keras.optimizers.Adam(0.01))
model.fit(X_train,Y_train,epochs=20,verbose=0)
model.evaluate(X_valid,Y_valid)

3.2 SimpleRNN

预测结果约为 mse=0.011左右，
只用一个RNN神经元的一层RNN，准确率不如线性回归。

#### simple RNN
model = keras.models.Sequential([
    keras.layers.SimpleRNN(1, input_shape=[None, 1])
])
model.compile(loss=keras.losses.mean_squared_error,
              optimizer=keras.optimizers.Adam(0.01))
model.fit(X_train,Y_train,epochs=20,verbose=0)
model.evaluate(X_valid,Y_valid)

3.3 多层 SimpleRNN

预测结果约为 mse=0.0037 。

#### deep rnn #1
model = keras.models.Sequential([
    keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
    keras.layers.SimpleRNN(20),
    keras.layers.Dense(1)
])
model.compile(loss=keras.losses.mean_squared_error,
              optimizer=keras.optimizers.Adam(0.01))
model.fit(X_train,Y_train,epochs=20,verbose=0)
model.evaluate(X_valid,Y_valid)

3.4 多层 LSTM

预测结果约为 mse=0.002 左右，要好于多层SimpleRNN

#### deep RNN:LSTM
model = keras.models.Sequential([
    keras.layers.LSTM(20, return_sequences=True, input_shape=[None, 1]),
    keras.layers.LSTM(20),
    keras.layers.Dense(1)
])
model.compile(loss=keras.losses.mean_squared_error,
              optimizer=keras.optimizers.Adam(0.01))
model.fit(X_train,Y_train,epochs=20,verbose=0)
model.evaluate(X_valid,Y_valid)

3.5 多层GRU

预测结果约为 mse=0.002 左右，和多层LSTM差不多。

# deep RNN:GRU
model = keras.models.Sequential([
    keras.layers.GRU(20, return_sequences=True, input_shape=[None, 1]),
    keras.layers.GRU(20),
    keras.layers.Dense(1)
])
model.compile(loss=keras.losses.mean_squared_error,
              optimizer=keras.optimizers.Adam(0.01))
model.fit(X_train,Y_train,epochs=20,verbose=0)
model.evaluate(X_valid,Y_valid)

4. 预测未来的10个值

亦即 Forecasting Several Time Steps Ahead。下述代码的预测误差mse比上述方法预测mse大，是因为预测未来的多个点是更困难的任务。

4.1 10次预测10个值:Sequence-to-Vector RNN

基本思路是要预测第10个点，先用模型预测未来的第1个点；然后未来的第1个点的预测值当做已知的，预测第2个点，以此类推…

下述代码中，预测结果取决于训练好的单个模型的准确度。

#### Forecasting Several Time Steps Ahead:forecast a point one time
series = generate_time_series(2000, n_steps + 10)
X_valid, y_valid = series[:, :n_steps], series[:,n_steps:]
X = X_valid
for step_ahead in range(10):
    y_pred_one = model.predict(X[:, step_ahead:])[:, np.newaxis, :]
    X = np.concatenate([X, y_pred_one], axis=1)
y_pred = X[:, n_steps:]
mse=keras.losses.mean_squared_error(y_valid,y_pred)
print(mse.numpy().mean())

4.2 1次预测10个值:Sequence-to-Vector RNN

将RNN的输出改为10，一次预测未来10个点，此时需要重新构造训练集：label变为10维。

下述代码，结果约为 mse=0.0188 左右。

#### Forecasting Several Time Steps Ahead:forecast 10 points one time,sequence-to-vector model
series = generate_time_series(10000, n_steps + 10)
X_train, Y_train = series[:7000, :n_steps], series[:7000, -10:, 0]
X_valid, Y_valid = series[7000:9000, :n_steps], series[7000:9000, -10:, 0]
X_test, Y_test = series[9000:, :n_steps], series[9000:, -10:, 0]
#
model = keras.models.Sequential([
    keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
    keras.layers.SimpleRNN(20),
    keras.layers.Dense(10)
])
model.compile(loss=keras.losses.mean_squared_error,
              optimizer=keras.optimizers.Adam(0.01))
model.fit(X_train,Y_train,epochs=20,verbose=0)
model.evaluate(X_valid,Y_valid)

4.3 1次预测10个值:Sequence-to-Sequence RNN

【自己的理解，供参考】4.2中损失函数计算时候最用了RNN最后输出的向量和标签来计算梯度优化模型，还可以更进一步。每一个time step都给模型一个标签，这样可以更充分的优化模型，进一步提高模型的准确率。此时需要重构标签：在4.2标签的基础上添加time step维度。

下述代码中，last_time_step_mse=0.0067 左右,要比4.2要好。

#### Forecasting Several Time Steps Ahead:forecast 10 points one time,sequence-to-sequece model
Y = np.empty((10000, n_steps, 10)) # each target is a sequence of 10D vectors
for step_ahead in range(1, 10 + 1):
    Y[:, :, step_ahead - 1] = series[:, step_ahead:step_ahead + n_steps, 0]
Y_train = Y[:7000]
Y_valid = Y[7000:9000]
Y_test = Y[9000:]
#
model = keras.models.Sequential([
    keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
    keras.layers.SimpleRNN(20, return_sequences=True),
    keras.layers.TimeDistributed(keras.layers.Dense(10))
])
def last_time_step_mse(Y_true, Y_pred):
    return keras.metrics.mean_squared_error(Y_true[:, -1], Y_pred[:, -1])
optimizer = keras.optimizers.Adam(lr=0.01)
model.compile(loss="mse", optimizer=optimizer, metrics=[last_time_step_mse])
model.fit(X_train,Y_train,epochs=20,verbose=0)
model.evaluate(X_valid,Y_valid)

4.4 1次预测10个值:1-d-CNN+Sequence-to-Sequence RNN

在4.3的模型开头加上一层1-d cnn，会提高准确率。

需要注意的是：输入维度为[7000,50,1]，经过下面代码中的CNN之后，输出的维度为[7000,24,20]（因为kernel_size=4,stride=2），这个维度再经过后面的两层SimpleRNN，模型的输出维度为[7000,24,10]，因此此时需要将原来的label（尺寸为[7000,50,10]），进行截取操作，由Ytrain[:, 3::2]之后，得到的维度就是[7000,24,10]。Y_valid同理。

下述代码中，last_time_step_mse=0.0039左右。

#### 1d-CNN+RNN
model = keras.models.Sequential([
    keras.layers.Conv1D(filters=20, kernel_size=4, strides=2, padding="valid",
    input_shape=[None, 1]),
    keras.layers.SimpleRNN(20, return_sequences=True),
    keras.layers.SimpleRNN(20, return_sequences=True),
    keras.layers.TimeDistributed(keras.layers.Dense(10))
])
model.compile(loss="mse", optimizer=keras.optimizers.Adam(0.01),metrics=[last_time_step_mse])
history = model.fit(X_train, Y_train[:, 3::2], epochs=20,verbose=0)
model.evaluate(X_valid,Y_valid[:, 3::2])

5. 总结

在本实验中：

（1）预测未来1个值的时候：LSTM和GRU预测准确度最高，线性回归训练速度比二者快一些；

（2）预测未来10个值的时候：准确率的关系CNN+RNN>S-to-S RNN> S-to-V RNN，而且CNN+RNN训练速度快一些。