回归预测 基于ELMAN递归神经网络预测及其matlab代码实现
文章目录
- 1. ELMAN神经网络的简介和算法描述
-
- 1.1 Elman网络介绍
- 1.2 Elman结构组成
- 1.3 ELMAN训练界面的参数解读
- 2. 建立ELMAN神经网络的步骤
- 3. 编写MATLAB代码
- 4. ELMAN程序运行结果
-
- 4.1 各层的神经元个数的确定过程
- 4.2 预测值和真实值的误差计算(SSE、MAE、MSE、RMSE、MAPE)
- 4.3 Elman网络预测的分析图像
- 5. 小结
- 6. MATLAB代码与数据下载地址
1. ELMAN神经网络的简介和算法描述
1.1 Elman网络介绍
神经网络是一个庞大的体系和概念,根据处理信息的不同方式来区分不同的network。比如根据处理信息结果的传递方向,分前馈型与反馈型。前馈型网络会根据输出数值来调整网络的参数,反馈型网络的输入会存在输入或者输出数值的反馈,可以对运算处理过程不断地进行优化。网络的反馈形式决定了网络的动态运算特点,递归神经网络ELMAN和前面所介绍的三层BP神经网络相比,增加了一个承接层,可以理解成延时算子,作用是让网络存在记忆功能,更好地适应数据输入的动态变化。
1.2 Elman结构组成
![]()
ELMAN的构造分为四层神经元:输入层、隐含层、承接层以及输出层(在使用智能算法优化ELMAN的参数时,理解ELMAN的结构将有所帮助)。
a). 输入层、输出层的神经元节点个数:
输入层的神经元数量与输入数据特征的维数是相等的,输出层的神经元节点数量也等同于输出数据标签的维度,这与BP神经网络一样。
b). 隐含层的神经元节点个数:
不管在BP还是ELMAN,或者其他的神经网络,隐含层的神经元个数都不是固定的。如果选择的隐含层神经元个数较少时,就会导致网络的学习程度减小甚至无法学习。节点个数较多时,则会导致网络训练的过程变慢,也很难得出预计的情况。只有当隐含层神经元数量只有控制在一个合理的范围内,才能使得网络模型好的进行学习运算。
通常的做法是根据以下公式来推出隐含层节点数目的范围,在范围之内根据训练误差最小(分类问题则取准确率最高或者误差率最低)的原则来确定最佳的隐含层节点数目。
h = m + n + a h=\sqrt{m+n}+a h=m+n+a
式中,h为隐含层节点个数,m为输入层节点个数,n为输出层节点个数,a一般取为1-10之间的常数。BP神经网络确定隐含层节点也通常采用该式。
c). 承接层的神经元节点个数:
承接层也叫做上下文层和状态层,主要功能是用来记忆隐含层上一个时间点的输出数值。所以承接层的神经元个数与隐含层相同,确定方法为:先根据训练误差最小确定最佳的隐含层神经元节点,再得到承接层的神经元节点个数。
1.3 ELMAN训练界面的参数解读
![]()
2. 建立ELMAN神经网络的步骤
1.读取数据
2. 划分训练集、测试集
3. 数据归一化
4. 获取输入层节点、输出层节点个数
5. 确定网络层与层之间的传递函数和训练算法
6. 构建最佳隐含层节点(承接层节点)的ELMAN神经网络
7. 训练网络
8. 网络测试
9. 对ELMAN的预测值与实际值进行误差分析
10. 打印预测结果和误差表格
3. 编写MATLAB代码
3.1 读取数据
采用深度学习常用的建筑物能源数据集进行预测实验,数据是EXCEL格式,形式为:
| 样本序号 | 输入指标1 | 输入指标2 | … | 输出指标 |
|---|---|---|---|---|
| 1 | - | – | – | – |
| 2 | - | – | – | – |
| … | - | – | – | – |
| n | - | – | – | – |
EXCEL的读取命令为(对应EXCEL的工作簿名,工作表Sheet名,单元格范围):
%% 读取数据
data=xlsread('数据.xlsx','Sheet1','A1:N252'); %%使用xlsread函数读取EXCEL中对应范围的数据即可
%输入输出数据
input=data(:,1:end-1); %data的第一列-倒数第二列为特征指标
output=data(:,end); %data的最后面一列为输出的指标值
3.2 划分训练集测试集
分层抽取即可,通过程序获取样本总数N,设置测试样本数目testNum,训练样本数为N-testNum。
N=length(output); %全部样本数目
testNum=30; %设定测试样本数目
trainNum=N-testNum; %计算训练样本数目
3.3 数据归一化
采用MATLAB自带的mapminmax函数,可以很方便的设置归一化的范围为[-1,1],[0,1]等(注意如果MATLAB安装了LSSVM的工具包,会与mapminmax函数发生冲突,在添加的路径中去掉LSSVM路径即可)
%% 数据归一化
%归一化到0,1之间,归一化可以消除特征指标的量纲和数量级的影响
[inputn,inputps]=mapminmax(input_train,0,1);
[outputn,outputps]=mapminmax(output_train);
inputn_test=mapminmax('apply',input_test,inputps);
3.4 获取输入层输出层节点的个数
使用size函数,用法为[M,N]=size(A),M对应A的行数,N对应A的列数,size(A,1)返回的M值,size(A,2)返回的N值。指标是列的方向,所以采用N=size(A,2)的写法。
inputnum=size(input,2);
outputnum=size(output,2);
3.5 确定网络的传递函数与训练算法
string={'tansig','purelin'}; %传递函数
func_str='traingdx'; %训练算法
3.6 使用循环遍历范围内的隐含层节点与训练误差情况
因为要找最小的误差,所以初始化训练误差时,将MSE设置较大的数字,用于在循环中确定最佳的隐含层节点。
%确定隐含层节点个数
%采用经验公式hiddennum=sqrt(m+n)+a,m为输入层节点个数
%n为输出层节点个数,a一般取为1-10之间的整数
MSE=1e+5; %初始化训练误差
3.7 训练网络
%% 构建最佳隐含层节点(承接层节点)的ELMAN神经网络
net=newelm(inputn,outputn,hiddennum_best,string,func_str);
% 网络参数
net.trainParam.epochs=1000; % 训练次数
net.trainParam.lr=0.01; % 学习速率
net.trainParam.goal=0.0001; % 训练目标最小误差
%% 训练网络
net=train(net,inputn,outputn);
3.8 网络测试与误差分析
%% 网络测试
an=sim(net,inputn_test); %用训练好的模型进行仿真
test_simu=mapminmax('reverse',an,outputps); % 预测结果反归一化
%% 对ELMAN的预测值与实际值进行误差分析
error=test_simu-output_test; %预测值和真实值的误差
%% 计算误差指标
SSE=sum(error.^2); %误差平方和
MAE=sum(abs(error))/len; %平均绝对误差
MSE=error*error'/len; %均方误差
RMSE=MSE^(1/2); %均方误差根
MAPE=mean(abs(error./output_test)); %平均百分比误差
4. ELMAN程序运行结果
4.1 各层的神经元个数的确定过程
![]()
![]()
4.2 预测值和真实值的误差计算(SSE、MAE、MSE、RMSE、MAPE)
![]()
4.3 Elman网络预测的分析图像
- 预测值和真实值的对比图像
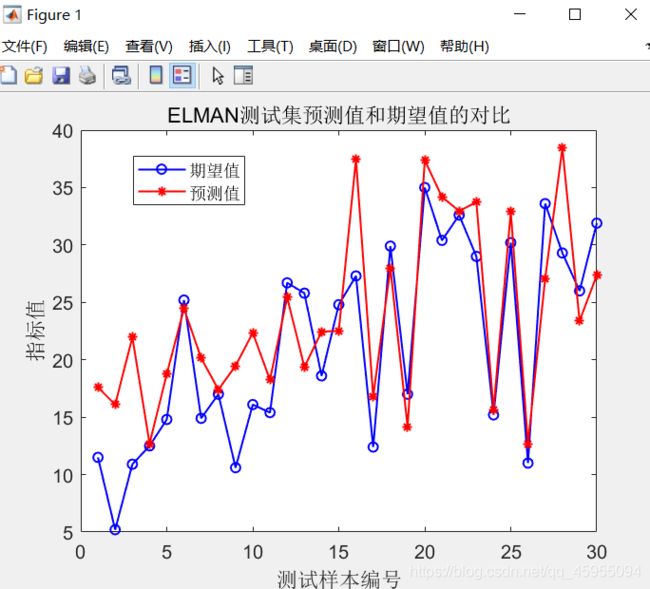
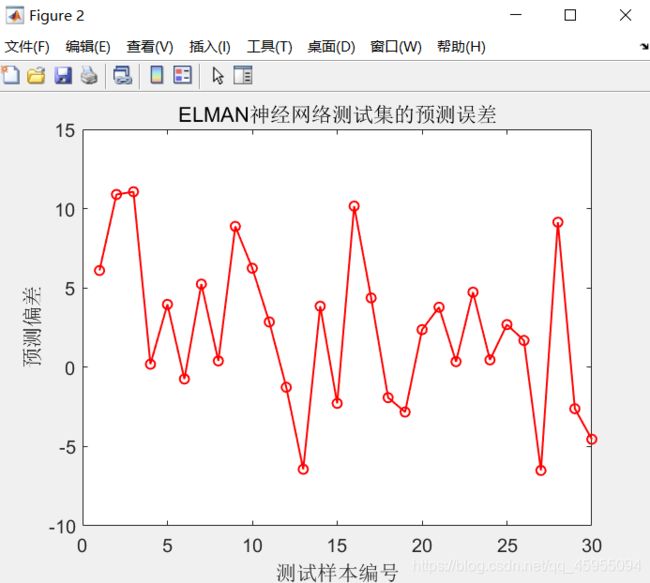
- 预测值与实际值的误差图像
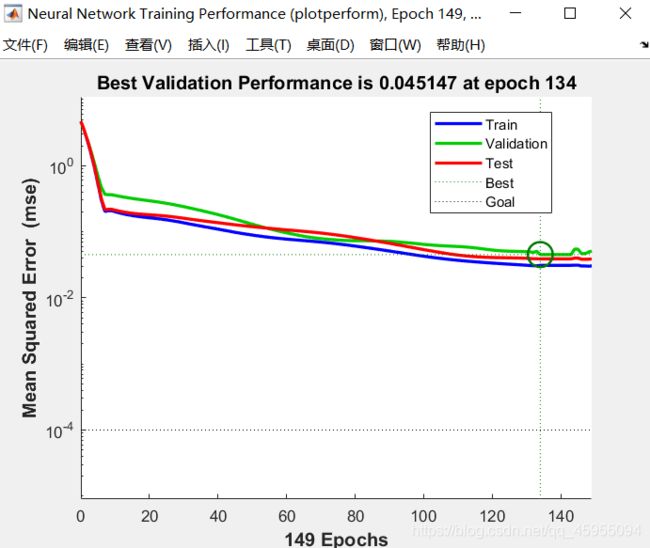
- 训练集、验证集、测试集和总体的均方误差随训练次数的变化图像
注:小圆圈位置代表终止的训练次数(即代数)处的均方误差
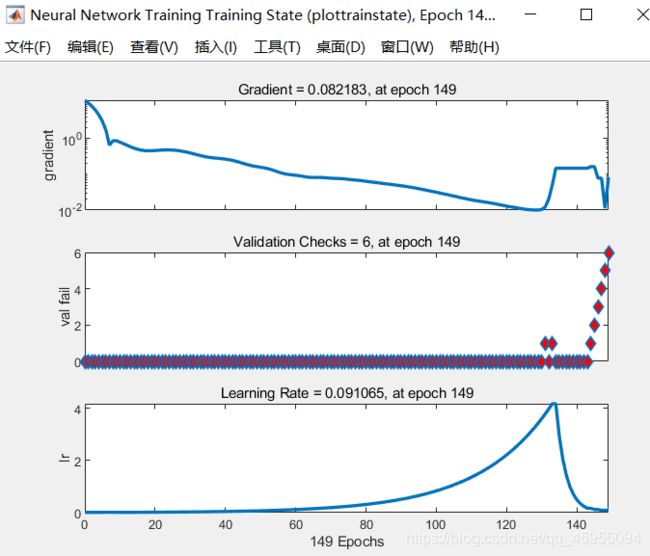
- Elman各阶段的训练图像
对三个图的解释:(1)梯度随训练的进行而发生减小,(2)在后期(149代)发生过拟合现象,连续6次过拟合,终止网络训练,(3)学习速率lr随训练的进行发生变化,减小。从前面3的train、test、validation来看,三个部分的训练性能变化一致,在134代训练达到最佳的训练效果(performance最小为0.04517),说明训练是合格的。过拟合现象在训练中无法避免,MATLAB进行Elman训练时,默认发生连续6次过拟合则停止训练,可设置过拟合连续的最大次数停止准则。
5. 小结
- Elman神经网络的结构相比BP神经网络多了一个承接层,能对动态变化的信息进行处理。
- 从Elman的四层结构来看,Elman有很好的自适应和学习能力,以及高并行度。
- 本篇将Elman神经网络的搭建思路和关键代码表述清楚,供大家参考和学习。如有问题,欢迎留言交流。
- 若有不恰当的地方,恳请码友指正。
6. MATLAB代码与数据下载地址
见博客主页