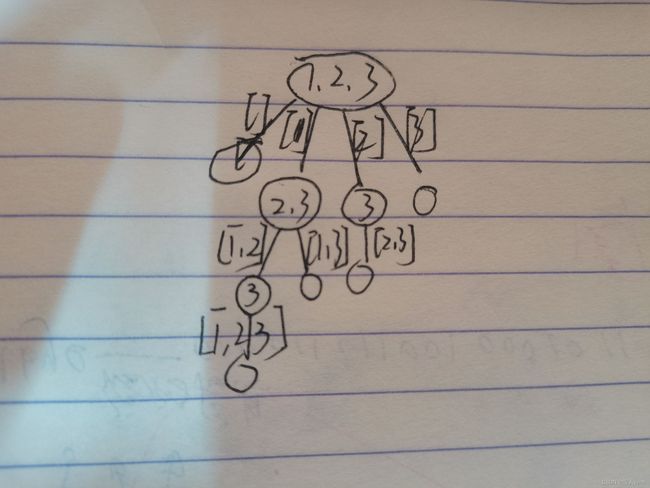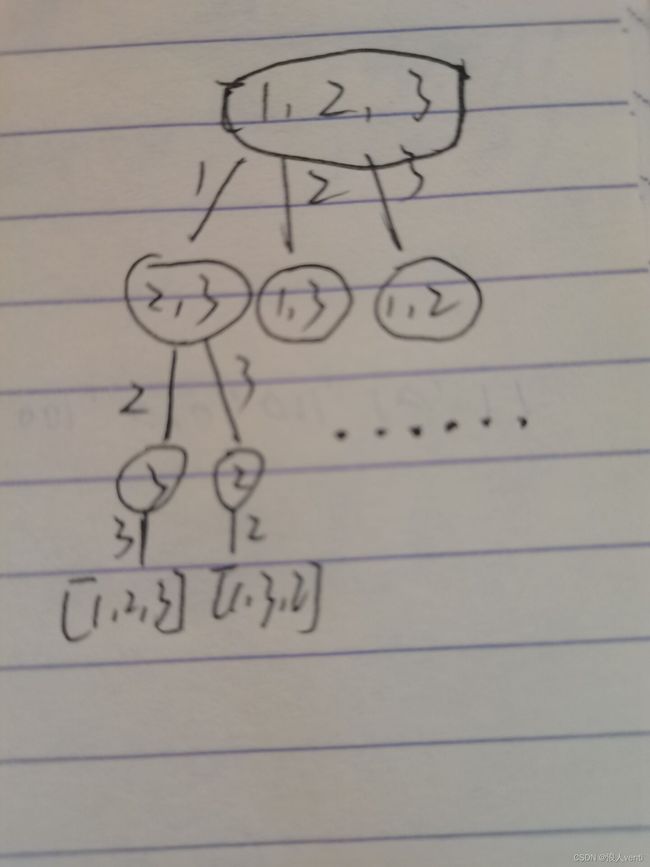深度优先搜索(DFS)-算法入门
深度优先搜索(DFS)-算法入门
DFS的主要六步
①递归树
②找结束条件(画出树后，结束条件比较好判断)
③找选择列表(看递归树)
④判断是否需要剪枝
⑤做出选择，递归调用，继续下一层递归
⑥撤销选择(回溯)
子集
题目描述：
给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
解决方案：
class Solution {
public:
vector<int> temp;
vector<vector<int>> res;
void dfs(vector<int> &nums, int start, int n){
res.push_back(temp);
for (int i = start; i < n; i++) {
temp.push_back(nums[i]);
dfs(nums, i + 1, n);
temp.pop_back();
}
}
vector<vector<int>> subsets(vector<int>& nums) {
int n = nums.size();
dfs(nums, 0, n);
return res;
}
};
六步法分析：
①画出递归树(需要一些回溯的基础思维)
②找结束条件，很显然为空结束，可以省略不写
③找选择列表，从图中可以看出是选择走过路径之后的数，解答中的for (int i = start; i < n; i++)
就是我们的选择列表，对应我们图中的同一层的路径选择
④剪枝，显然图中的路径都是我们所需要的答案，所以不需要剪枝
⑤操作后递归，将路径保存，之后递归进入下一层
⑥回溯操作，相当于撤销该层的操作，与第⑤步中的操作反着来就可
如果我们的集合有重复元素？又该如何处理呢？
输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]
解决方案：
class Solution {
public:
vector<int> temp;
vector<vector<int>> res;
void dfs(vector<int> nums, int start, int n) {
res.push_back(temp);
for (int i = start; i < n; i++) {
if (i != start && nums[i] == nums[i - 1]) continue;
temp.push_back(nums[i]);
dfs(nums, i + 1, n);
temp.pop_back();
}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
int n = nums.size();
sort(nums.begin(), nums.end());//与剪枝配套使用
dfs(nums, 0, n);
return res;
}
};
具体分析和上一题差不多，但是不一样的是需要我们去剪去一些不必要的分枝，如图
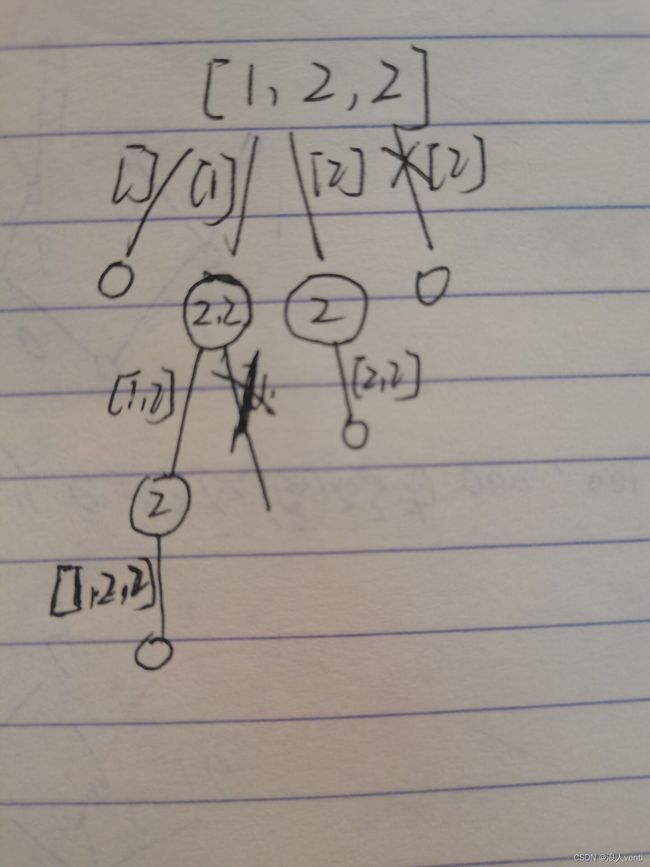
那么我们第④步的剪枝该怎么做呢，我们先需要对数组进行预处理，排序，让我们相同的值，挨在一起，当
if (i != start && nums[i] == nums[i - 1]) continue;就不用往下递归
以下有一些组合的题目，和子集类似，第⑤步稍有不同，直接贴题目和解决方案
组合
输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。
class Solution {
public:
vector<int> path;
vector<vector<int>> res;
int cnt = 0;
void dfs(vector<int> nums, int start, int n, int target) {
if (cnt == target) {
res.push_back(path);
return;
}
for (int i = start; i < n; i++) {
if (cnt > target) continue;
cnt += nums[i];
path.push_back(nums[i]);
dfs(nums, i, n, target);//从i开始不用，满足题目重复选择
path.pop_back();
cnt -= nums[i];
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
int n = candidates.size();
dfs(candidates, 0, n, target);
return res;
}
};
当然还有不能重复使用的，剪枝方案和子集一样，排序后，相邻元素相同的枝条剪去。
全排列
题目描述：
给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
class Solution {
public:
bool visited[6];
vector<int> path;
vector<vector<int>> res;
void dfs(vector<int>& nums, int depth, int n) {
for (int i = 0; i < path.size(); i++) cout<<path[i]<<" ";
cout << endl;
if (depth == n){
res.push_back(path);
return;
}
for (int i = 0; i < n; i++) {
if (!visited[i]){
path.push_back(nums[i]);
visited[i] = true;
dfs(nums, depth + 1, n);
visited[i] = false;
path.pop_back();
}
}
}
vector<vector<int>> permute(vector<int>& nums) {
int n = nums.size();
dfs(nums, 0, n);
return res;
}
};
分析：
因为全排列的题目，有顺序要求，所以选择列表不能，再选路径之后的数，我们需要要用一个visited数组来标记一个元素是否被访问过，本题不需要剪枝。
输入：nums = [1,1,2]
输出：
[[1,1,2],
[1,2,1],
[2,1,1]]
同样的问题如果有重复元素该怎么办？还用之前的if (i != start && nums[i] == nums[i - 1]) continue;能行吗？看上去貌似可以，但是我们还需要添加一个条件if (i != start && nums[i] == nums[i - 1] && !visited[i - 1]) continue; 保证上一个元素是否被访问过，如果是即使相同也不能被减去，否则会出错，可以自行画递归树，或者调试感受。
总结
DFS的基本思考方式就是这些了，不过还有许多很难的搜索题目，需要我们去灵活运用这些基本方法，加以改进，递归的整个过程是人脑不可视的，通俗来讲，就是递归树我们的大脑很难整个去了解它的具体结构，我们往往是通过一些简单的例子去画出一个递归树，然后去揣摩它接下来的发展情况，写出代码，感觉上有点像数学上的归纳推理，所以我们没有必要去想象它整个运行的具体情况，这很费脑，也没有必要，从局部出发，推理全局。这里许多内容都借鉴了leetcode某位大佬的思想，大家也可以去大佬写的题解处看看
大佬的题解
以上题目均来自leetcode