深度优先搜索(dfs),宽度优先搜索(bfs),深度优先遍历,宽度优先遍历
图的遍历:我们希望从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次。
通常有两条遍历图的路径(对有向图和无向图都适用):①深度优先搜索 ;② 广度优先搜索。
一,DFS(深度优先搜索)
深度优先搜索(暴搜):一条路走到黑
1,树(排列数字为例)
如下图所示。
所谓深搜就是一条路走到黑。以上面的排列数字n=3为例,依次从第一层向下,直到三个位置均满之后,再回溯到上一层,再判断是否下一层还有遗漏情况。也符合字典序要求。
注意,为了避免同一顶点被访问多次,每次每层用过了一个点,需要通过辅助数组(初始值置为“假”或“零”)给该点标记一下(值变为“真”或“一”),说明已经用过。此外也需要对排列路径进行一个记录。但是一次深搜之后还需还原现场(即将标记过的点还原),以便于能继续回溯之后的搜索。
代码:
#include
using namespace std;
const int N=8;
int path[N],st[N];//path数组存路径,st数组表示访问标志数组。
int n;
void dfs(int u)
{
if(u==n)
{
for(int i=0;i>n;
dfs(0);
return 0;
} 2,图(n皇后为例):
图的深度遍历:
无向图深搜:
有向图深搜:
例题:
剪枝:提前判断当前路径是否合法,不合法提前回溯。
n皇后问题就是满足n*n的数组中,放n个皇后,并且这n个皇后不能同一列,同一行,同一对角线,同一反对角线。所以,基于全排列问题,我们再多加上对角线和反对角线即可。那么对角线和反对角线如何处理呢?
如下图所示:
代码:
#include
using namespace std;
const int N=20;
char g[N][N];//存图;
int col[N],dg[N],udg[N];//col表示列,dg正对角线,udg反对角线;
int n;
void dfs(int u)
{
if(u==n)
{
for(int i=0;i>n;
for(int i=0;i 总结:解决回溯问题,实际上就是一个决策树的遍历过程。回溯算法核心就是for循环里面的递归,在递归之前"做选择",递归之后"撤销选择”。回溯算法就是纯暴力枚举,复杂度一般都很高。
二,BFS(广度优先搜索)
bfs核心算法思想:把一些问题抽象成图,从一个点开始,向四周扩散。
一般来说bfs算法都是用“队列”这种数据结构,每次将一个节点周围的所有节点加入队列。
使用队列:与树的层序遍历类似,越是接近根节点越早遍历。
实质:从起点到终点寻找最短路径。
例题:
1,走迷宫
分析:寻找从左上到右下的最短路径。
代码:
#include
#include
#include
#include
using namespace std;
typedef pairPII;
const int N=110;
queueq;//存图上某点坐标;
int g[N][N];//存图;
int d[N][N];//存路径上的距离;
int m,n;
int bfs()
{
memset(d,-1,sizeof d);
q.push({0,0});//第一个点为起点并且标记走过;
d[0][0]=0;
while(!q.empty())
{
auto t=q.front();
q.pop();
int dx[4]={0,1,0,-1};
int dy[4]={1,0,-1,0};
for(int i=0;i<4;i++)
{
int x=t.first+dx[i],y=t.second+dy[i];
if(x=0&&y=0&&g[x][y]==0&&d[x][y]==-1)
{
d[x][y]=d[t.first][t.second]+1;
q.push({x,y});
}
}
}
return d[n-1][m-1];
}
int main()
{
cin>>n>>m;
for(int i=0;i>g[i][j];
}
}
cout< 2,八数码问题
分析:类似于小时候玩的拼图游戏。
首先将输入的一串字符(最开始的状态)存入队列,判断这种状态是否符合题目条件(“12345678x”的状态)即可。
实现该条件存在的问题有:
①状态表示复杂;
处理方案:将3*3的二维数组转化为一维数组;
②记录状态距离困难。
处理方案:将一维数组作为key值,状态改变次数作为value存入哈希表,每改变一次状态,value加一,直到变成状态”12345678x“,如果到达不了最终状态则返回-1;
代码:
#include
#include
#include
#include
using namespace std;
int bfs(string s)
{
queueq;
unordered_mapd;
q.push(s);
d[s]=0;
string end="12345678x";
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
while(!q.empty())
{
string t=q.front();
q.pop();
if(t==end)return d[t];
int distant=d[t];
int k=t.find('x');
int x=k/3,y=k%3;
for(int i=0;i<4;i++)
{
int a=x+dx[i],b=y+dy[i];
if(a>=0&&a<3&&b>=0&&b<3)
{
swap(t[k],t[a*3+b]);
if(!d.count(t))
{
d[t]=distant+1;
q.push(t);
}
swap(t[k],t[a*3+b]);
}
}
}
return -1;
}
int main()
{
string s;
for(int i=0;i<9;i++)
{
char a;
cin>>a;
s+=a;
}
cout< 三,深度优先遍历
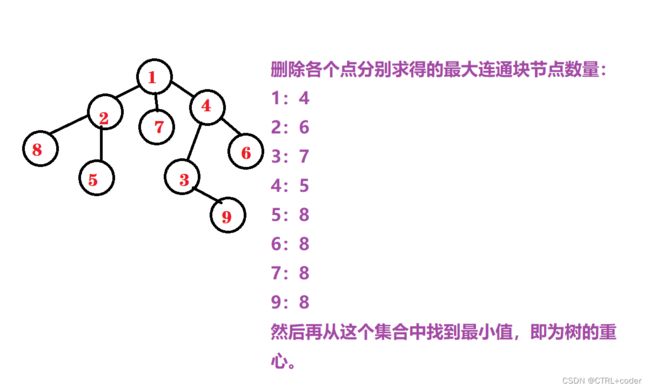
例题:树的重心
题目分析:
如图为题目样例,最后结果应该是最小值4 。
那么我们应该如何处理这道题呢?
可以利用深搜。我们以删除节点4为例,删除节点4,会生成除了4以外的三个连通子图,分别是以3为根节点的一个子树,以6为根节点的子树以及上面那一块(以1为节点但需要除去以4为根节点的子树)。如图:
我们可以利用深搜算出4下面子树节点数量,至于上面那块,由于深搜是一条路走到黑,不会回头,所以可以利用最大的树节点数量减去已知的子树节点数, 即为上面那块未知节点数量。
代码:
#include
#include
#include
#include
using namespace std;
const int M=100010;
const int N=2*M;
int st[M],h[M],e[N],ne[N],idx;
int ans=M,n;
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int dfs(int u)
{
st[u]=1;//标记u已遍历;
int res=0;
int sum=1;
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];
if(st[j])continue;
int s=dfs(j);
res=max(res,s);//求删除u节点时,u节点的下方连通子树中节点的最大值。
sum+=s;//包含u节点总子树;
}
res=max(res,n-sum);//上面求得的所有子树中的连通块最大值再跟上方那块比较,求得整棵树的最大连通块最大值。
ans=min(ans,res);//寻找删除各个不同节点的情况下最大值中的最小值;
return sum;//每次返回子树节点数
}
int main()
{
memset(h,-1,sizeof h);
cin>>n;
for(int i=0;i>a>>b;
add(a,b);
add(b,a);
}
dfs(1);
cout< 四,宽度优先遍历
例题:图中点的层次
题目分析:
n个点m条边的有向图,求出节点1到n的最短距离。
看到最短距离,应该想到bfs,bfs通常是用队列实现。
从1开始遍历即可,最后返回n的距离。
代码:
#include
#include
#include
#include
using namespace std;
const int N=100010;
int e[N],h[N],ne[N],idx,n,m;
int d[N];
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int bfs()
{
queueq;
memset(d,-1,sizeof d);
d[1]=0;
q.push(1);
while(q.size())
{
auto t=q.front();
q.pop();
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(d[j]==-1)
{
d[j]=d[t]+1;
q.push(j);
}
}
}
return d[n];
}
int main()
{
memset(h,-1,sizeof h);
cin>>n>>m;
while(m--)
{
int a,b;
cin>>a>>b;
add(a,b);
}
cout<