神经网络与深度学习 作业4：第四章课后题
目录
- 五道习题
-
- 习题4-2
- 习题4-3
- 习题4-7
- 习题4-8
- 习题4-9
- 参考文献
- 心得体会
五道习题
习题4-2
试设计一个前馈神经网络来解决XOR问题,要求该前馈神经网络具有两个隐藏神经元和一个输出神经元,并使用ReLU作为激活函数。
1、XOR问题介绍
所谓XOR问题就是异或问题，（数学符号为“ ⨁ \bigoplus ⨁”，程序符号为“^”）不要被这个名字唬住了。我这里简单介绍一遍。
| 异或真值表 | ||
| 输入 | 输出 | |
| A | B | A XOR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
2、XOR问题的网络结构
代码实现如下：
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
class XORModule(nn.Module):
def __init__(self):
super(XORModule, self).__init__()
self.fc1 = nn.Linear(2, 2) # 输入层和隐藏层
self.fc2 = nn.Linear(2, 1) # 隐藏层和输出层
self.relu = nn.ReLU()
def forward(self, x):
x = x.view(-1, 2)
x = self.relu((self.fc1(x)))
x = self.fc2(x)
return x
# 输入和输出数据
input_x = torch.Tensor([[0, 0], [0, 1], [1, 0], [1, 1]])
input_x1 = input_x.float()
real_y = torch.Tensor([[0], [1], [1], [0]])
real_y1 = real_y.float()
# 设置损失函数和参数优化函数
net = XORModule()
loss_function = nn.MSELoss() # 用交叉熵损失函数会出现维度错误
optimizer = optim.SGD(net.parameters(), lr=0.5) # 用Adam优化参数选不好会出现计算值超出0-1的范围
# 进行训练
for epoch in range(100):
out_y = net(input_x1)
loss = loss_function(out_y, real_y1) # 计算损失函数
optimizer.zero_grad() # 对梯度清零，避免造成累加
loss.backward() # 反向传播
optimizer.step() # 参数更新
# 输出权值和偏置
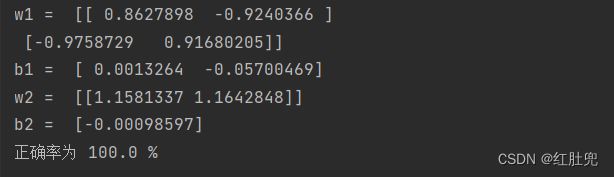
print('w1 = ', net.fc1.weight.detach().numpy())
print('b1 = ', net.fc1.bias.detach().numpy())
print('w2 = ', net.fc2.weight.detach().numpy())
print('b2 = ', net.fc2.bias.detach().numpy())
# 测试
input_test = input_x1
out_test = net(input_test)
a = np.around(out_test.detach()).numpy().tolist()
b = real_y1.numpy().tolist()
count = 0
for i in range(4):
if a[i] == b[i]:
count += 1
print("正确率为", count*100/4, "%")
输出如果如下：
习题4-3
试举例说明“死亡ReLU问题”，并提出解决方法。
ReLU函数梯度只可以取两个值：当输入小于0时，梯度为0；当输入大于0时，梯度为1。在反向传播过程中，如果学习率比较大，一个很大的梯度经过ReLU神经元，可能会导致ReLU神经元更新后的梯度是负数，进而导致下一轮正向传播过程中ReLU神经元的输入是负数，输出是0。由于ReLU神经元的输出为0，在后续迭代的反向过程中，该处的梯度一直为0，相关参数不再变化，从而导致ReLU神经元的输入始终是负数，输出始终为0。即为“死亡ReLU问题”。
解决办法：
使用Leaky ReLU(带泄露的ReLU函数)替换掉ReLU函数。
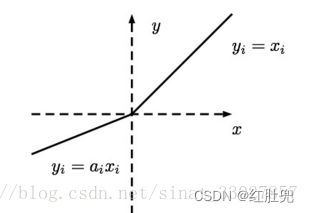
a i a_i ai一般取值为0.01。这样的好处就是：在反向传播过程中，对于LeakyReLU激活函数输入小于零的部分，也可以计算得到梯度，而不至于陷入“死亡”。
习题4-7
为什么在神经网络模型的结构化风险函数中不对偏置进行正则化？
下面三个图分别代表欠拟合，合适的拟合效果，过拟合。
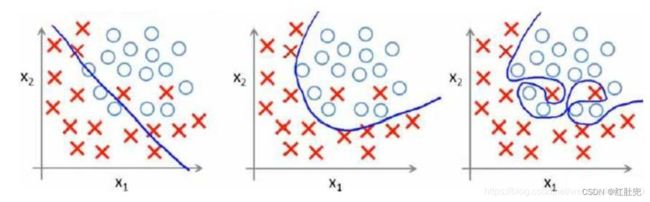过拟合原因：
- 数据噪声太大
- 特征太多
- 模型太复杂
而正则化就是用来防止模型过拟合而采取的手段。
我们在数据集上的结构化风险函数为
R ( W , b ) = 1 N ∑ n = 1 N L ( y ( n ) , y ^ ( n ) ) + 1 2 λ ∣ ∣ W ∣ ∣ F 2 R(W,b)=\frac{1}{N}\sum^N_{n=1}L(y^{(n)},\hat{y}^{(n)})+\frac{1}{2}λ||W||^2_F R(W,b)=N1n=1∑NL(y(n),y^(n))+21λ∣∣W∣∣F2
其中 1 2 λ ∣ ∣ W ∣ ∣ F 2 \frac{1}{2}λ||W||^2_F 21λ∣∣W∣∣F2就叫做正则化项。
在神经网络模型的结构化风险函数中加入正则化项，可以避免过拟合，而过拟合一般表现为模型对于输入的微小改变产生了输出的较大差异，模型对异常点非常敏感（即准确插入异常点），导致拟合函数中的曲率过大，这主要是由于有些参数w过大的关系，通过对||w||进行惩罚，可以缓解这种问题。
对偏置b进行正则化貌似对防止过拟合没有什么影响，不管b的输入改变是大还是小，参数b也就只是作为一个偏置而已，但是w会对不同的数据产生不一样的加权。作为一个数，当对输入进行求偏导时偏置b不会进入计算，对模型的构建几乎没有贡献，因此正则化偏置b对避免过拟合没有太大的意义。
习题4-8
为什么在用反向传播算法进行参数学习时要采用随机参数初始化的方式而不是直接令 w = 0 , b = 0 w = 0, b = 0 w=0,b=0？
反向传播就是要将神经网络的输出误差，一级一级地传播到输入。在计算过程中，计算每一个w对总的损失函数的影响，即损失函数对每个w的偏导。根据w的误差的影响，再乘以步长，就可以更新整个神经网络的权重。当一次反向传播完成之后，网络的参数模型就可以得到更新。更新一轮之后，接着输入下一个样本，算出误差后又可以更新一轮，再输入一个样本，又来更新一轮，通过不断地输入新的样本迭代地更新模型参数，就可以缩小计算值与真实值之间的误差，最终完成神经网络的训练。
当直接令w=0，b=0时，在误差反向传播中，所有的权重值都会进行相同的更新。比如，在2层神经网络中，假设第一层和第二层的权重为0，这样一来，正向传播时，因为输入层的权重为0，所以第二层的神经元全部会被传递相同的值。第二层的神经元中全部输入相同的值，这意味着反向传播时第二层的权重会全部都会进行相同的的更新。因此，权重会被更新为相同的值，并拥有了对称的值（重复的值）。这使得神经网络拥有许多不同的权重的意义丧失了。为了防止“权重均一化”，必须随机生成初始值。
习题4-9
梯度消失问题是否可以通过增加学习率来缓解?
在神经网络中，当前面隐藏层的学习速率低于后面隐藏层的学习速率，即随着隐藏层数目的增加，分类准确率反而下降了。这种现象叫做消失的梯度问题。
梯度更新公式：
w = w − η ∂ E k ∂ w h j w=w-\eta \frac{\partial E_{k} }{\partial w_{hj}} w=w−η∂whj∂Ek
梯度消失就意味着 ∂ E k ∂ w h j \frac{\partial E_{k} }{\partial w_{hj}} ∂whj∂Ek越来越趋近于0，导致 w w w更新速度变慢，从而使训练时间变长。增大学习率就是增大 η \eta η的值，从而使 w w w更新的快一些。适当地怎么增大学习率是完全可行的，但一定要注意学习率不可过大，不然容易导致梯度爆炸。
参考文献
MarkDown 常用语法
激活函数Relu 及 leakyRelu
一篇文章完全搞懂正则化（Regularization）
心得体会
这次作业又复习了一下markdown的用法，正所谓温故而知新，现在果然又懂了好多操作。表格和缩进以及字体的颜色大小的设置等，但是在表格中，不知为何打不上公式，我本想在表格中打入" ⨁ \bigoplus ⨁"符号，但试了好久，也搜了好多博客，还是打不上，鼓捣了一个多小时还是放弃了，只好用了“XOR”。感觉时间又花在了无用的地方。这次作业又看了好多书上以前没有看到的知识，还是很有收获的。