冈萨雷斯《数字图像处理》学习笔记（十）图像分割

目录

序言

一、点、线和边缘检测

1、背景知识

2、孤立点的检测

​3、 线检测

​4、边缘模型

5、基本边缘检测

​6、更先进的边缘检测技术

​7、边缘连接和边界检测

二、阈值处理

1、基本的全局阈值处理

​2、用Otsu方法的最佳全局阈值处理

​三、区域分割

1、基于区域的分割

​2、用形态学分水岭的分割

3、分割中运动的应用

---

序言

本章中的多数分割算法均基于灰度值的两个基本性质之一：不连续和相似性。对于不连续的灰度，方法是以灰度突变为基础分割一幅图像，例如边缘。对于相似的灰度，主要方法是根据一组预定义的准则把一幅图像分割为相似的区域，例如阈值处理、区域增长、区域分裂和区域聚合。

主要内容：■间断的检测
                       ■点检测、线检测、边缘检测
                  ■边缘连接和边界的检测
                       ■局部处理、整体处理
                  ■基于门限的分割方法
                       ■全局门限、自适应门限
                  ■基于区域的分割方法
                       ■区域生长、分离与合并
                  ■基于形态学分水岭的分割方
                       ■水坝构造、分水岭算法

一、点、线和边缘检测

1、背景知识

一阶导数：

 
 
二阶导数： 

 在增强细节方面，二阶导数远强于一阶导数： 
1. 一阶导数通常在图像中产生较粗的边缘； 
2. 二阶导数对精细细节，如细线、孤立点和噪声有较强的响应； 
3. 二阶导数在灰度斜坡和灰度台阶过渡处会产生双边缘响应； 
4. 二阶导数的符号可用于确定边缘的过渡是从亮倒暗还是从暗到亮。

2、孤立点的检测

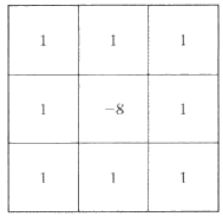
孤立点的检测应以二阶导数为基础，使用拉普拉斯算子： 
 

拉普拉斯算子

特点:
   ■中心为正，邻近为负;模板和为0
   ■对噪声敏感、产生双象素宽边缘，没有方向信息

用途:
   ■少用于边缘检测
   ■常用于在边缘已知情况下，确定像素在明区或暗区。

3、 线检测

线检测同样可以使用拉普拉斯模板，但拉普拉斯检测子是各向同性的，因此其响应与方向无关，也可以使用与方向有关的改进算子： 

4、边缘模型

1.台阶模型
2.斜坡模型
3.屋顶边缘模型 

一阶导数的幅度可用于检测图像中的某个点处是否存在一个边缘。二阶导数的符号可用于确定一个边缘像素是位于该边缘的暗侧还是亮侧。二阶导数的附加性质：对图像中的每条边缘，二阶导数生成两个值；二阶导数的零交叉点可用于定位粗边缘的中心。 

5、基本边缘检测

梯度及性质

梯度算子
一维模板： 
 

Roberts： 
  
 

Prewitt： 
 
  

Sobel： 
 
 
 
用于检测对角线边缘的Prewitt和Sobel： 

6、更先进的边缘检测技术

Marr-Hildreth边缘检测器
高斯拉普拉斯LoG： 
 

坎尼边缘检测器

7、边缘连接和边界检测

理想情况下，边缘检测应该仅产生位于边缘上的像素集合。实际上，由于噪声、不均匀照明引起的边缘间断，以及其他引入灰度值虚假的不连续的影响，这些像素并不能完全描述边缘特性。因此，一般是在边缘检测后紧跟连接算法，将边缘像素组合成有意义的边缘或区域边界。

8、霍夫变换（边界搜索的变换法）

■点-线的对偶性质
    ■图象空间XY里所有过点(x, y)的直线，其方程为
                                   y= px+ q
    ■将上述方程转换为参数PQ空间，其表达式为
                                   q=-px+y

■图像空间XY中-条直线上的点，在参数空间PQ中都过点(Pr q)

■点-线对偶
    ■图象空间中共线的点曰参数空间里相交的线
    ■参数空间中相交于同1个点的直线白图象空间里共线的点

■哈夫变换思路
    ■把在图象空间中直线的检测问题转换到参数空间里,
    ■通过在参数空间里进行简单的累加统计完成检测任务

■具体方法
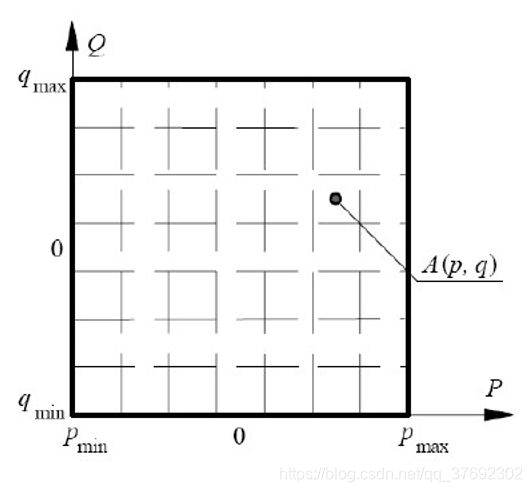
    ■  在参数空间PQ里建立1个2-D的累加数组A( p, q)
    ■P是XY空间直线的斜率
    ■q是XY空间直线的截距
    ■数组大小根据对待检测线段的斜率和截距的估计来确定    
    ■p∈[，]
    ■q∈[， ]
    ■累加方式
    ■A(p,q)=A(p,q) +1
    ■A( p, q)值:共线点数
    ■(p, q)值:直线方程参数
■根据A( p, q)大小检测线段
   

■直线变换到霍夫空间的点

    ■实际中的变换不采用斜率和截距

    ■应用直线的极坐标描述方式

■直线的检测

 

 

 

 

 

二、阈值处理

图像阈值处理在图像分割应用中处于核心地位。

1、基本的全局阈值处理

2、用Otsu方法的最佳全局阈值处理

三、区域分割

1、基于区域的分割

区域生长
区域增长包含的三个条件为：（1）选定增长的起始点（核）；（2）确定增长的规则；（3）确定增长的结束条件。 

举个栗子：

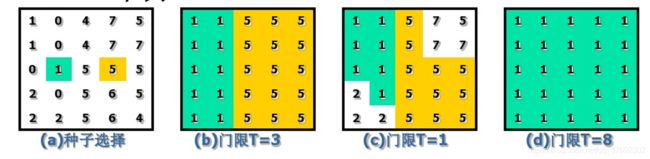
■首先确定可被区分的区域数量，并选定种子像素
■根据相邻像素之间的灰度相似性，确定是否可以属于同一类别
■对每一像素都经过这样的判断就可以结束分割过程
■决定是否属于同一区域的灰度判定方式不同，分割结果不同

■种子的选取方法
     ■根据图像直方图，波峰数目代表图中目标的数目
     ■波峰位置的灰度是目标的平均灰度。种子灰度

■区域生长的判据
     ■根据直方图，波峰之间的灰度差别可以作为生长判据
     ■如果区域具有纹理特征，还可以引入纹理判据进行判断
     ■可以根据对目标的先验知识(形状、大小等)来约束区域生长的过程

区域分割与聚合

基本思路：首先将图像分隔为初始区域，然后分裂和合并这些区域直到获得均匀区域为止。

基本步骤:   ■初始分隔:一 分为二(或一分为四) ;
                  ■计算区域方差;
                  ■将方差大的区域继续划分，方差小的区域与邻域比较考虑合并。

 

举个栗子：

 

■首先将图像一分为四;
■一个区域不必再分，其他继续一分为四;
■余下两个还需再分，其他可以根据灰度相似性判断门限决定是否合并(本例分别合并绿色和白色区域)
■没有需要再分的区域，根据相似性合并所有可能的子区域

2、用形态学分水岭的分割

基本概念

■同一目标，有相近的灰度，有相邻的空间位置

■灰度类比高程，可用地形学来理解图像的目标

     ■地形学中的汇水盆地类比目标（均匀的低灰度区）

     ■地形学中的分水岭类比目标之间的分割线（突变的高灰度区）

■目标的灰度并非都是最低值，分析的对象转换到梯度图像，更符合地形学的概念

分水岭算法的思想

■在梯度图像上分析
■梯度值低的位置为中心，逐步向周边高梯度位置扩展
    ■采用形态学膨胀的方式扩充空间连续的位置
    ■同时受约束于图像的高梯度区域
■扩展的同时遇到多区域交汇，交汇的位置就形成了分割的边界(分水岭、水坝)

分水岭分割算法
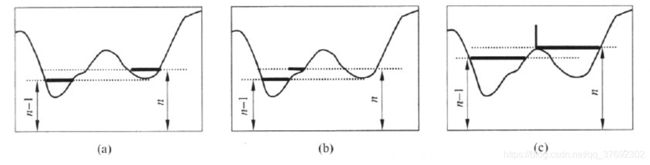
■符号定义
     ■梯度小于n的全部像素集合T(n)
     ■包含梯度小于n的第i个区域的像素集合C;(n)
■初始化:
     ■根据T(min+1)得到初始k个区域Ci(min+1)， i= 1,2,..k
■算法递归(以第n步为例)
     ■梯度递增，分析范围扩大T(n)→T(n+1)
     ■各个区域膨胀，C;(n)→C,(n+1)， i=1,2,..k
     ■新增加的范围内，其像素q必定属于以下三种情况之一

■对情况（a），产生新区域，q为其中元素

■对情况（b），q合并到相应的区域

■对情况（c）。q为所属区域之间的分割线（分水岭）

■分水岭算法的问题
    ■  梯度图对噪声敏感，直接分割容易造成过分割
    ■太多的分割区域使得其结果没有实用价值
■解决办法
    ■对梯度图像先行滤波;
    ■应用标记的方法

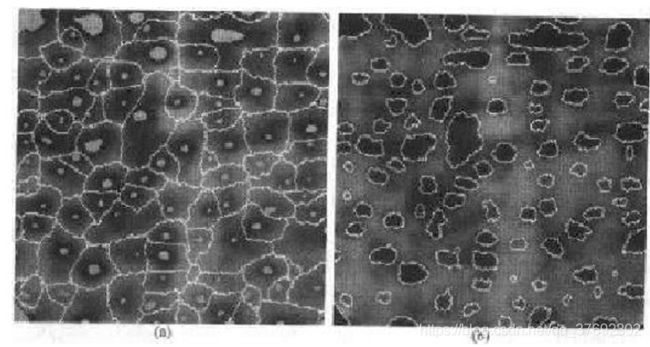
应用标记
■图像中指定区域的种子
     ■被更高‘海拔’包围、区域内部连通、具有相同灰度
■在种子的基础上使用分水岭算法，过程中不再产生新区域，对算法中情况(a)的像素做不归类处理，直到全部像素都分配到相应区域，形成前期分割结果
■在前期分割结果的每个区域内，再进行目标/背景区分,得到最后的目标分割

3、分割中运动的应用

见课本！！！