图像处理学习笔记-09-形态学图像处理

预备知识

讨论的对象是二值图像中白色像素的集合，每一个元素是像素的坐标

• 空集：任何空集都只是同一个集合，记作$\Phi$
• 子集、并集、交集、补集、集合的差
• 集合$B$的反射表示为$\hat{B}$，集合的映像，也就是集合中的每一个元素$(x,y)$被$(-x,-y)$替代，也就是旋转180度
  $$\hat{B}=\{w|w=-b,b\in B\}$$
• 集合的平移表示为$(B{)}_z$，也就是每一个点$(x,y)$替换为$(x+z_1,y+z_2)$
• SE结构元：一个处理的模板，用来探测图像的一个小的集合或者子图像

腐蚀和膨胀

腐蚀

$B$对$A$的腐蚀表示为：
$$A\ominus B=\{z|(B{)}_z\subseteq A\}$$
也就是一个用$z$平移的$B$，使得$B$包含在$A$中的$z$的集合，假定$B$是一个结构元，因为$B$包含在$A$中等价于$B$不和背景共享任何公共元素，所以也可以表示为：
$$A\ominus B=\{z|(B{)}_z\cap A^c=\varnothing \}$$
腐蚀操作可以看做是形态学滤波操作，这种操作将小于结构元的图像细节从图像中滤除，主要过程是用结构元素0、1构成的模板与图像做卷积，结果等于模板和的值的点就是腐蚀的结果
用$3\times 3$的结构元的时候，物体的边界沿周边减少一个像素，可以消除掉图像中小于结构元大小的目标物体，平滑物体边界，如果物体之间有细小的连通，选择适当的结构元可以将物体分开，断开狭长的连接，去除细长的突出物，不同的结构元及其不同的原点产生不同的结果

膨胀

$B$对$A$的膨胀定义为：
$$A\oplus B=\{z|(\hat{B})z\cap A\ne \varnothing \}$$
也就是使得$\hat{B}$的平移和$A$至少有一个交集的$z$的集合，上式可以等价为：
$$A\oplus B=\{z|[(\hat{B}{)}_z\cap A]\subseteq A\}$$
上式和卷积操作类似，但是需要注意的是膨胀是一个非线性操作，因为是以集合操作为基础的，但是卷积操作是一个线性操作，主要过程是用结构元素0、1构成的模板与图像做卷积，所有大于0的地方就是膨胀结果
膨胀的作用是当使用$3\times 3$的结构元的时候，在物体的边界沿周边增加一个像素、将目标周围的背景点合并到目标中，平滑物体边界，将不同的目标连通到一起，填补分割后物体的孔洞

对偶性

腐蚀和膨胀运算对于求补运算和反射运算是对偶的：
$$\begin{gathered} (A\ominus B{)}^c=A^c\oplus \hat{B} \\ (A\oplus B{)}^c=A^c\ominus \hat{B} \end{gathered}$$
上述性质对于$B$是对称的时候非常有效，此时先求补再膨胀等价于先腐蚀再求补

开运算和闭运算

之前的腐蚀和膨胀操作存在改变图像大小的问题，但是开操作和闭操作则不会，开操作和闭操作都会平滑物体的轮廓，但是开操作会断开窄桥，消除细的突出物，但是闭操作会消除小空洞连接窄桥
先开运算后闭运算构成噪声滤波器，首先开运算消除背景噪声但是图片产生间断，之后开运算消除噪声斑点，连接间断

• 开操作：先腐蚀后膨胀
  $$A\circ B=(A\ominus B)\oplus B$$
  满足如下性质：
  $A\circ B$是$A$的一个子集，如果$C$是$D$的一个子集，那么$C\circ B$是$D\circ B$的一个子集，$(A\circ B)\circ B=A\circ B$
• 闭操作：先膨胀再腐蚀
  $$A\cdot B=(A\oplus B)\ominus B$$
  满足如下性质
  $A$是$A\cdot B$的一个子集，如果$C$是$D$的一个子集，那么$C\cdot B$是$D\cdot B$的一个子集，$(A\cdot B)\cdot B=A\cdot B$
• 对偶性：
  $$\begin{gathered} (A\cdot B{)}^c=(A^c\circ \hat{B}) \\ (A\circ B{)}^c=(A^c\cdot \hat{B}) \end{gathered}$$

击中或击不中变换

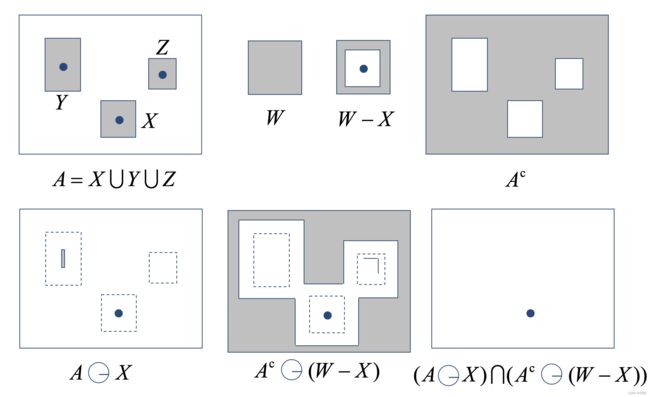
如上图所示，集合$A$由$X,Y,Z$三个子集构成，现在的目的是找到$X$的位置，方法就是击中操作，令$B=(B_1,B_2),B_1=X,B_2=(W-X)$，最后得到$X$的位置的集合操作公式就是：
$$Ao\ast B=(A\ominus X)\cap [A^c\ominus (W-X)]$$
根据对偶性，可以将上式写为：
$$Ao\ast B=(A\ominus B_1)\cap (A\oplus {\hat{B}}_2)$$
上面两个式子就称为形态学击中或击不中变换，上面的式子基于一个假设，也就是当物体之间是断开的，且物体至少被一个像素宽的背景围绕，物体才可分

一些基本的形态学算法

边界提取

先腐蚀然后减去得到的就是边界
$$\beta (A)=A-(A\ominus B)$$

区域填充

$X_k=(X_{k-1}\oplus B)\bigcap A^c,k=1,2,3$，当$X_k=X_{k-1}$的时候迭代终止，$X_0$是要填充的区域的内部的任意一点

连通分量提取

$X_k=(X_{k-1}\oplus B)\bigcap A,k=1,2,3,\cdots$，当$X_k=X_{k-1}$的时候迭代终止，$X_0$是物体内部的任意一点

孔洞填充

一个孔洞被定义为由前景像素相连接的边界所包围的一个背景区域：
$$X_k=(X_{k-1}\oplus B)\cap A^c,k=1,2,3\cdots$$
当$X_k=X_{k-1}$的时候算法迭代停止，$A$表示的是一个集合，元素是包含一个孔洞的边界，集合$X_k$包含所有被填充的孔洞，$X_0$表示的是初始的孔洞集合的原点位置

连通分量的提取

$A$是包含一个或多个连通分量的集合：
$$X_k=(X_{k-1}\oplus B)\cap A$$

凸壳

如果在集合$A$内连接任意两个点的直线段都在$A$的内部，就称集合$A$是凸形的，任意集合$S$的凸壳$H$是包含$S$的最小凸集，集合差$H-S$称为$S$的凸块，求解凸壳过程如下：

首先反复对$B^1$进行击中或击不中变换直到没有变化然后与$A$求并得到一个集合，这个过程同样对$B^i$重复(应用于$A$)于是得到4个集合，得到的四个集合求并即为$A$的凸壳。

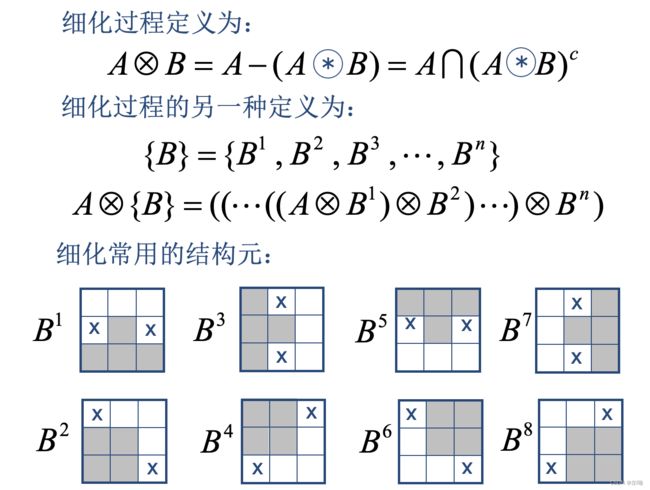
细化

粗化

粗化和细化是形态学上的对偶过程，为了将集合粗化，先求集合的补，通过对集合补的细化后，对细化结果求补，最后消除间断即获得集合的粗化

骨架

集合$A$的骨架表示为$S(A)$，可以通过下式计算：
$$\begin{gathered} S(A)=\bigcup _{k=0}^K{S}_k(A) \\ {S}_k(A)=(A\ominus kB)-(A\ominus kB)\circ B \end{gathered}$$
其中$B$表示一个结构元，$(A\ominus kB)$表示对$A$进行连续$k$次腐蚀，$K$是$A$被腐蚀为空集之前的最后一次腐蚀：
$$K=max\{k|(A\ominus kB)\ne \varnothing \}$$

实现1-细化

在不破坏连通性的背景下细化图像

• 做腐蚀操作但是不立即删除像素，只打标记
• 将不破坏连通性的标记点删除
• 重复执行，将产生细化结果

实现2-距离变换图算法

距离变换图算法把二值图像变换为灰度图像，其中每个像素的灰度值等于0到他最近的1的距离

算法流程：

• 求取二值图像的边界
• 对边界二值图像求取距离变换
• 求距离变换图中的局部极大值
• 落入原二值图像中的局部极大值就是图像的骨架

裁剪

对细化和骨架绘制算法的补充，清除这些算法产生的一些不必要的附加成分

• 用一系列被设计用来检测终点的结构元素对A进行细化得到结果$X_1$
• 得到$X_1$的终点集合$X_2$
• 对端点$X_2$进行三次膨胀处理，结果和原图求交$X_3$
• 最终结果是$X_3\bigcup X_1$

灰度级图像的形态学

膨胀

$$(f\oplus b)=max\{f(s-x,t-y)+b(x,y)|(s-x),(t-y)\in D_f,(x,y)\in D_b\}$$
膨胀图像明亮且暗小的细节减弱或消除

腐蚀

$$(f\ominus b)=min\{f(s+x,t+y)-b(x,y)|(s+x),(t+y)\in D_f,(x,y)\in D_b\}$$
腐蚀图像变暗且尺寸小的明亮细节减弱或消除

开运算和闭运算

开运算：先腐蚀后膨胀，小的明亮的细节变小，而暗的细节没有明显变化
闭运算：先膨胀后腐蚀，小的暗的细节变小，但明亮部分没有明显变化

应用

形态学图像平滑

先开运算后闭运算，减少或除去人为明和暗的因素和噪声

形态学图像梯度

膨胀减去腐蚀图像
$$g=(f\oplus b)-(f\ominus b)$$

高帽变换

原图减去开运算结果，增强阴影的细节