R 利用回归分析与时间序列预测北京市PM2.5

注：代码全部在最后,数据来源UCI,链接如下：

https://archive.ics.uci.edu/ml/datasets/Beijing+PM2.5+Data

摘要

现代社会科技进步，人们的生活质量逐步提高，但伴随着各类工业和科技的发展，环境问题凸显，最初人们粗放式的经济发展方式在一定程度上对环境造成不可逆转的破坏。在各种环境污染问题，空气污染问题又是如今人们关注的重中之重。北京是我国首都，同时也是我国空气污染较为严重的几个北方城市之一，因此关注北京市空气污染情况是我国观测空气污染情况的重要关注对象之一。在本文中，首先，我就北京市PM2.5及其他污染物和气象情况的近几年观测数据做出相应回归分析，建立回归模型试图利用已知的其他污染物和气象情况信息对PM2.5做出预测；其次，利用现如今已观察到的数据做单变量时间序列分析，寻找其变化规律、做简单预测，为北京市人民规划出行做好提前空气质量预警。

关键词：PM2.5 多元回归分析 时间序列分析

 

一、数据集介绍

该数据集来自于北京市环境检测中心，包括了2013年3月1日到2017年2月28日，12个国家控制的空气质量监测站每小时的空气污染数据，且每个空气质量站点的气象数据都与中国气象局站相匹配。此空气污染数据集包括12个站点数据集，每个数据集包括了35064个时间数据，共有（35064*12）个样本。

变量包括：PM2.5、PM10、SO2（二氧化硫）、NO2（二氧化氮）、CO（一氧化碳）、O3（臭氧）为空气污染物；剩余变量TEMP（温度）、PRES（大气压）、DEWP（露点温度）、RAIN（降雨量）、WD（风向）、WSPM（风速）天气情况。

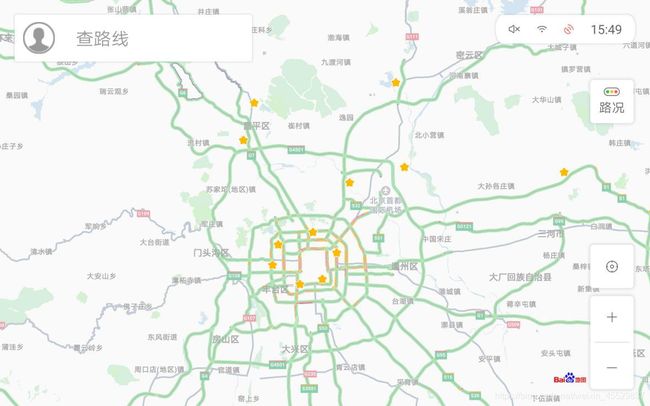
站点包括：万寿西宫（西城区）、官园（西城区）、万柳（海淀区）、天坛（东城区）、农展馆（朝阳区）、奥体中心（朝阳区）、怀柔、古城（顺义区）、顺义、东寺（平谷区）、定陵（昌平区）、昌平共十二个，其地理位置分布如下：

 

二、研究问题一

（一）研究问题

将SO2、NO2、CO、O3、TEMP（温度）、PRES（大气压）、DEWP（露点温度）、RAIN（降雨量）、WD（风向）、WSPM（风速）作为解释变量，Y作为被解释变量，以预测误差最小为原则，选择最优多元回归模型。

（二）研究方法

多元回归

（三）研究步骤

1.数据集选择

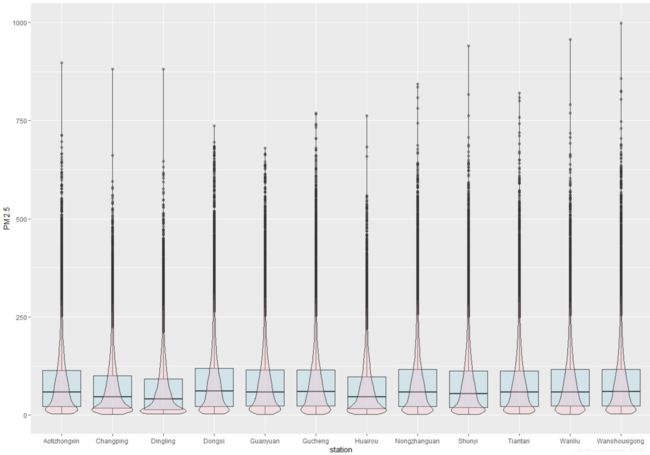
由于该数据集有北京12个观测点的完整时间数据，以下以PM2.5为例绘制出PM2.5分布的盒图和小提琴图，并按照均值从从低到高排列，发现12个观测点PM2.5的分布基本相似，以下选择其中一个地区奥体中心的数据集进行分析。

2.数据可视化

    在进行定量建模之前，先绘制图像对变量分布和变量之间的相关关系进行直观感受与定性分析。

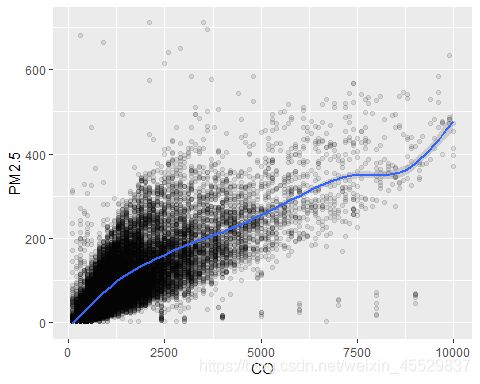
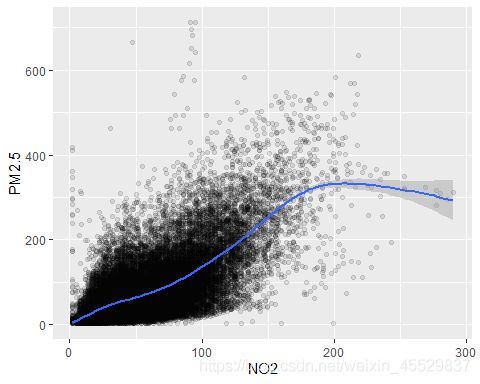
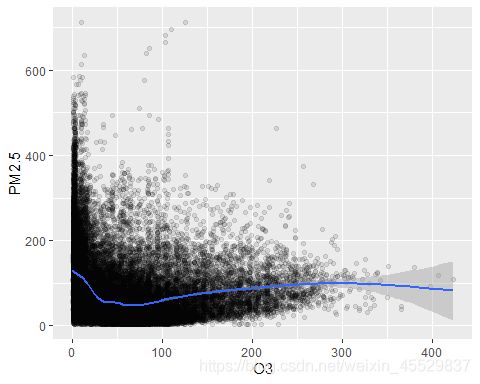
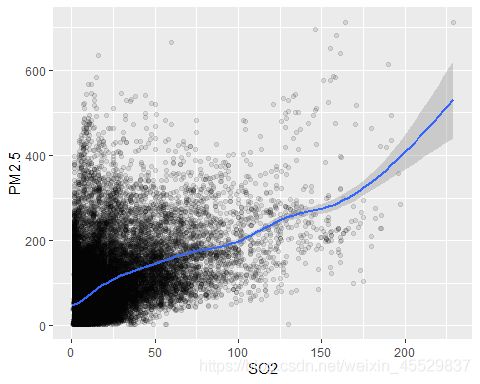
观察SO2、NO2、CO和O3这四种污染物分别与PM2.5的相关关系：

可以看出PM2.5随着CO、NO2浓度的上升而呈线性上升趋势，O3和SO2和PM2.5的线性关系没有那么强烈。

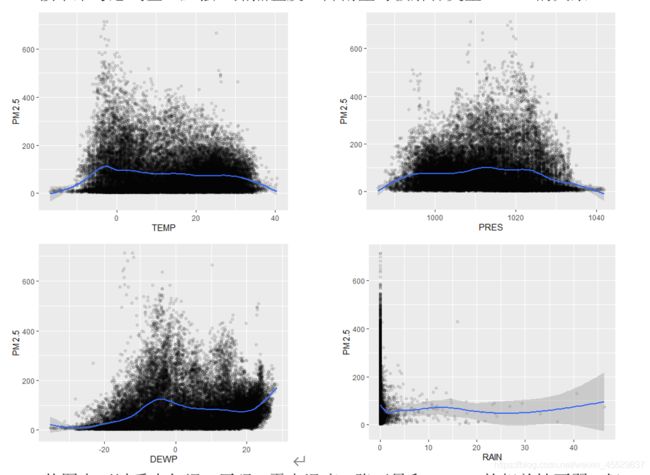
接下来考虑气温、压强、露点温度、降雨量与被解释变量PM2.5的关系：

从图中可以看出气温、压强、露点温度、降雨量和PM2.5的相关性更弱，但具体会对PM2.5的预测有怎样的效果，需要在回归模型中进一步分析。

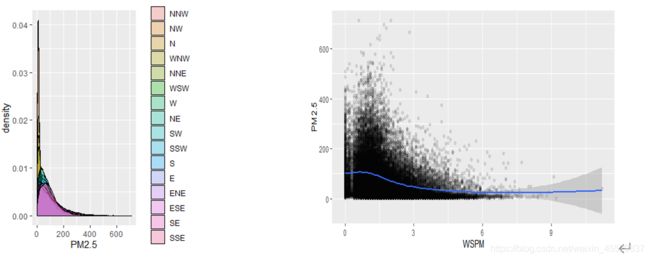
最后考虑风速和风向与被解释变量PM2.5的关系：

   在第一幅图可以看中，图例从上到下以PM2.5均值大小排序，可以看出西北方向的风PM2.5峰度高且整体分布靠左，东南方向的风峰度低而整体分布靠右，也就是PM2.5值整体偏大；风速和PM2.5的线性相关关系不是很明显。

3.回归分析（以奥体中心为例）

（1）前期准备

① 对待选入模型的变量进行平稳性检验，防止出现伪回归，使用ADF单位根检验，拒绝原假设，不存在单位根，序列平稳。

② 对所选的“奥体中心”数据做删失处理，由于数据量足够多，直接删除带有缺失值的行。

（2）变量选择：

先做全变量回归，发现有大量变量存在系数t检验结果不显著，并且存在VIF值较高的变量，需要进行变量选择，这里尝试了两种变量选择的方法，两种方法筛选出的变量相同。

① 根据BIC准则做逐步回归，依次从全模型剔除变量，直至BIC值最小。

② 利用10折交叉验证，将数据根据被解释变量均匀分为10份，每一份分别当作测试集，计算利用10个训练集训练出的模型在相应测试集上的MSE并取平均，建立循环寻找使得交叉验证所得MSE平均值最小的变量组合，即预测效果最好的变量组合。

（3）回归结果：

Coefficients:                    

	Estimate	Std. Error	t value	Pr(>|t|)
(Intercept)	232.812250	64.033810	3.636	0.000278	***
SO2	0.463988	0.019179	24.192	<2e-16	***
NO2	0.710602	0.015931	44.605	<2e-16	***
CO	0.035909	0.000440	81.608	<2e-16	***
O3	0.249223	0.009159	27.211	<2e-16	***
TEMP	-1.154538	0.086582	-13.335	<2e-16	***
PRES	-0.255064	0.062654	-4.071	4.7e-05	***
DEWP	1.612418	0.061157	26.365	<2e-16	***
RAIN	-1.605167	0.413330	-3.883	0.000103	***
WSPM	5.117095	0.378114	13.533	<2e-16	***
wdENE	-3.069006	1.125061	-2.728	0.006382	**
wdN	3.049390	1.506081	2.025	0.042913	*
wdNNW	4.275978	1.719299	2.487	0.012891	*
wdSE	5.081616	1.756569	2.893	0.003822	**
wdSSE	4.561950	2.014055	2.265	0.023523	*
wdSSW	3.442118	1.493166	2.305	0.021165	*
wdW	-5.690030	1.895453	-3.002	0.002687	**
wdWSW	-3.425869	1.428746	-2.398	0.016505	*

其拟合优度及显著性水平检验结果如下表：

Residual standard error	42.81 on 15891 degrees of freedom
Multiple R-squared	0.7164
Adjusted R-squared	0.7161
F-statistic	2361 on 17 and 15891 DF
p-value	< 2.2e-16

（4）模型检验：

a. 独立性检验：拒绝原假设rho==0，认为随机扰动项存在自相关；

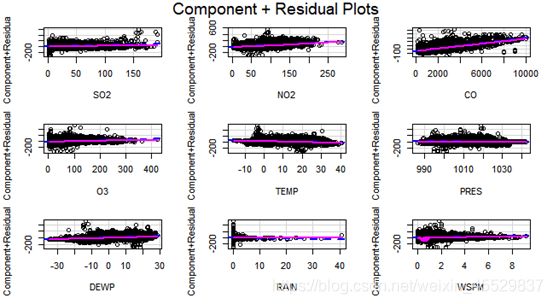
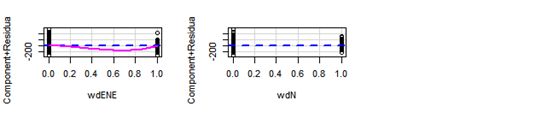
b. 线性性检验：由图可以看出RAIN不是线性的；

 

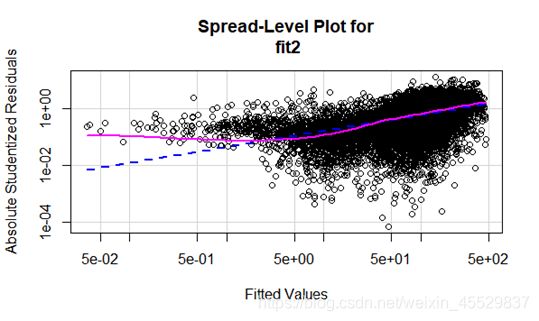
c.同方差检验：拒绝原假设（方差恒定），模型存在异方差；

 

d.多重共线性检验:

下表计算了变量选择之后建立的回归模型的各解释变量的VIF

SO2	NO2	CO	O3	TEMP	PRES
1.658091	2.978911	2.513574	2.442158	8.321385	3.619437
DEWP	RAIN	WSPM	wdENE	wdN	wdNNW
6.036338	1.027168	1.801353	1.102301	1.064934	1.105588
wdSE	wdSSE	wdSSW	wdW	wdWSW	-
1.047875	1.042624	1.091834	1.033414	1.057227	-

 

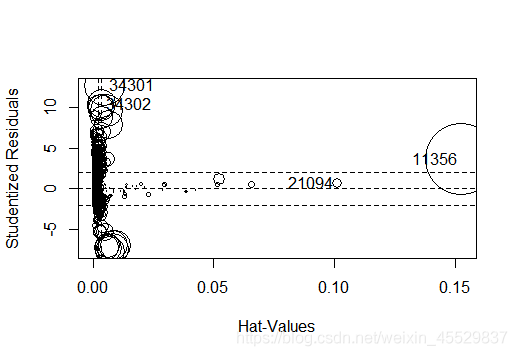
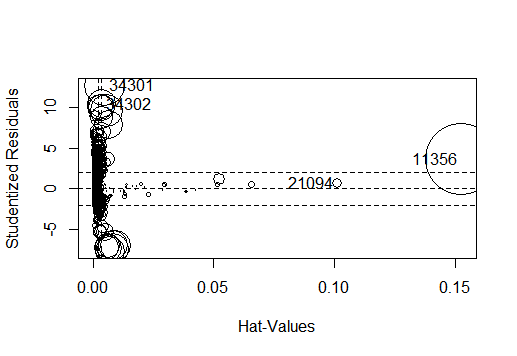
e.鉴别强影响点与离群点：由结果得只有10个离群点和4个强影响点，相对于样本观测值数量而言极小，可忽略其影响；

 

 

（4）模型修正

    虽然对于用于预测的模型来说，自相关性和异方差的存在对预测没有影响，但是自相关性和异方差会影响回归模型的解释性，所以以下给出两种模型修正方法。

① 对数变换

对全部大于0的变量直接取对数，对大于等于0的变量，把0替换为0.01再取对数，对存在负值的变量和哑变量不取对数，再进行线性回归。

结果没有消除自相关和异方差，方法失效；

② NeweyWest方法

虽然自相关和异方差性不会影响参数估计的无偏性，但是会低估参数的标准误差，使得系数的显著性检验失效。此处利用NeweyWest方法修正标准误差，得到各解释变量真实的显著性水平：

 

t test of coefficients:

	Estimate	Std.Error	t value	Pr(>|t|)
(Intercept)	232.8122503	219.5400294	1.0605	0.288954
SO2	0.4639883	0.1171078	3.9621	7.463e-05	***
NO2	0.7106023	0.0699557	10.1579	<2.2e-16	***
CO	0.0359093	0.0027966	12.8404	<2.2e-16	***
O3	0.2492227	0.0246035	10.1296	<2.2e-16	***
TEMP	-1.1545382	0.2041962	-5.6541	1.594e-08	***
PRES	-0.2550644	0.2146604	-1.1882	0.234764
DEWP	1.6124182	0.1631761	9.8815	<2.2e-16	***
RAIN	-1.6051674	0.6104286	-2.6296	0.008557	**
WSPM	5.1170951	0.5528738	9.2554	<2.2e-16	***
wdENE	-3.0690056	1.3442140	-2.2831	0.022436	*
wdN	3.0493905	2.1257378	1.4345	0.151447
wdNNW	4.2759783	1.7114650	2.4984	0.012484	*
wdSE	5.0816158	2.1300002	2.3857	0.017057	*
wdSSE	4.5619502	2.3059688	1.9783	0.047910	*
wdSSW	3.4421184	2.0387166	1.6884	0.091359	.
wdW	-5.6900301	2.0368072	-2.7936	0.005219	**
wdWSW	-3.4258687	2.0828541	-1.6448	0.100032

 

（四）结果分析：

从总体效果：所拟合模型修正后可决系数为0.7161，模型整体拟合优度较好，且各系数显著性较好；

从污染物角度：可以看出在SO2、NO2、CO和O3这四种污染物当中，NO2对PM2.5的影响最为严重，其次是SO2，接下来是O3，相对而言CO对PM2.5的影响最小因此我们应该重点关注于SO2和NO2的治理。比如涉及SO2和NO2排放的污染源或行业包括火电、石油炼制、有机化工、钢铁、有色等，所以可以考虑这类行业的污染检测或者技术革新；

从天气角度：当风向靠近西或者北时，PM2.5的密度曲线会更高更靠近0，当风向靠近南或者东时，发生PM2.5较大的事件的频率就会变高，而实际生活中大风可使空气流动性增强，污染物不易滞留，因此达到驱霾的目的，而北京的西北风往往是来自蒙古西伯利亚高压带，风力往往比东南风强，故驱霾效果更好，数据与生活经验相符。

 

 

 

 

 

三、研究问题二

（一）研究问题

分析北京市奥体中心2013年1月到年月日的PM2.5存在的变化规律，并试图用分析结果对PM2.5的变化情况进行短期预测。

（二）研究方法

采用ARIMA模型、指数平滑模型时间序列分析。

（三）研究步骤

1.前期准备

（1）平稳性检验：

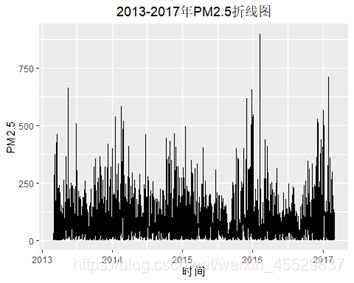
用于时间序列建模的数据必须是平稳的，从下面的2013-2017年PM2.5折线图可以看出序列大致平稳，同时在研究问题一中我们已经对序列做了ADF检验，结果是序列平稳。

（2）缺失值处理：

由于时间序列分析需要完整的观测，因此采用KNN方法补齐缺失值

（3）观察序列季节性特征：

从上面的时间序列折线图能大概看出PM2.5具有秋冬高、春夏低的季节性变化，对数据进行更多的可视化以探求其他季节性特征。

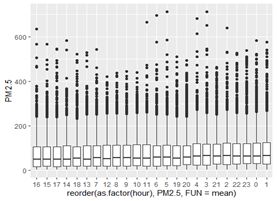
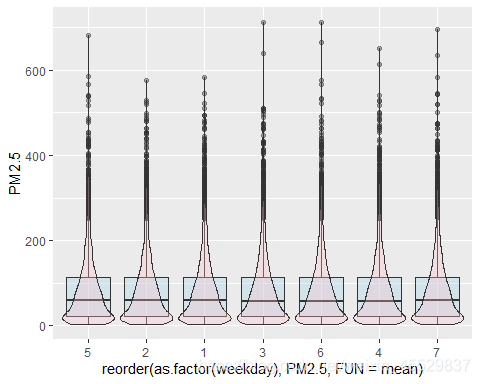
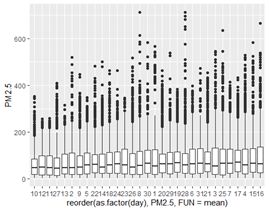
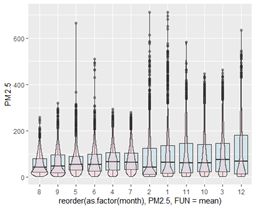
以下四张图分别为按几时、星期几、一个月中的第几天和几月绘制的盒图，并将盒图按均值排序，可以看出只有小时（第一幅图）和月份（第四副图）具有较为明显的季节性趋势，因此接下来我们重点考察以24个小时和一年（8766个小时）为周期的季节性变化。

 

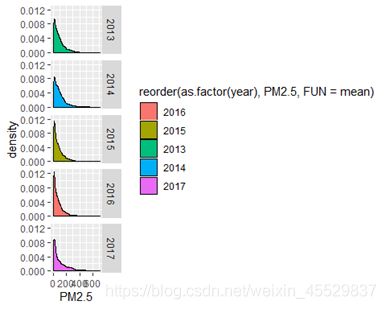
（4）观察序列长期趋势：

分别绘制2013-2017年PM2.5的密度分布曲线如下，可以看出从2013年到2016年，PM2.5的分布逐年向左，即PM2.5值总体上变小，预测这是因为2017年的样本只有1-2月，为冬季样本，和全年PM2.5分布可能会有偏差。

2.建立ARIMA模型

（1）定阶：

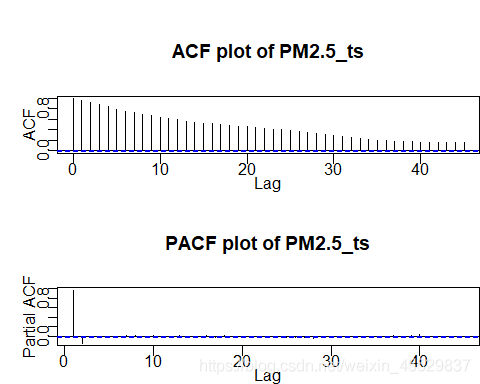
①自相关系数、偏自相关系数定阶：ACF图和PACF图分别如下，自相关系数和偏相关系数都呈拖尾，该序列不是AR模型，也不是MA模型，观察截尾定阶的方法失效。

②BIC准则定阶：

R语言中存在两个函数都是利用BIC准则最小来定阶，由于其原理不同就分别尝试。

a. armasubsets函数

该函数使用长自回归法，使用足够高阶的AR模型来逼近任意平稳序列，先估计逆转形式的参数，近似的求出原模型参数的估计值，可初步判断出模型为带有均值项的ARMA(13,23)过程，同时R给出该定阶结果的BIC值为93000。

1. auto.arima函数

该函数的原理是傅里叶展开的时间序列频域分析法，组合不同频率不同周期的波，并且支持带有季节性趋势的时间序列拟合，所以分别尝试不带季节性趋势序列的auto.arima拟合和以24小时为季节性周期的auto.arima拟合。

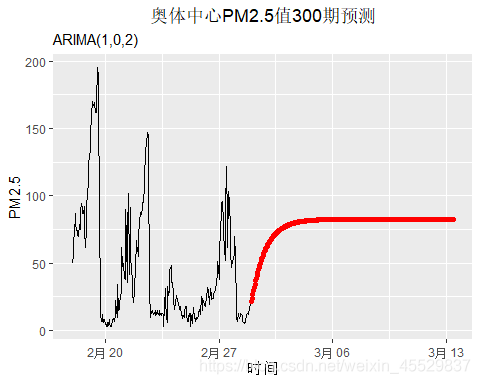
1. 不带季节性趋势定阶结果：ARIMA(1,0,2)
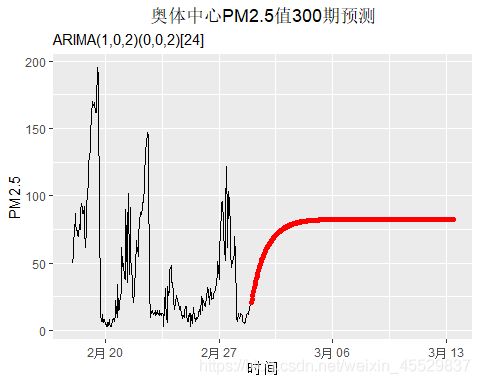
2. 带季节性趋势定阶结果：ARIMA(1,0,2)(0,0,2)[24]

（2）参数估计：

在没有先验分布的情况下，采用最小二乘法分别对上面两个已经定阶的模型进行参数估计，结果如下。

模型①无季节性因子

模型②有季节性因子，以一天（24h）为周期

  

（3）残差检验：

进行Box Test，其中box.test函数需要参数lag,对于模型①，使用MA部分的阶数2，对于模型②，根据forecast包的作者Rob J Hyndman的书Forecasting : Principles and Practice中的建议，当拟合模型具有季节性变化时，且以m为周期时，参数lag设置为2m。

对于模型①，p>0.05，不拒绝原假设，认为是白噪声；

对于模型②，p<0.05,拒绝原假设，认为不是白噪声。

ARIMA(1,0,2)模型类型	χ2	df	P值
无季节性因子（模型①）	0.0040207	2	0.998
有季节性因子（模型②）	28721	48	< 2.2×10-16

（4）预测：

PM2.5值的300阶预测结果分别如下，两种ARIMA模型的预测效果相当，差别极其细微；可以看出模型只能预测出一小截趋势，当预测阶数再增加时，只能预测出均值。

3.指数平滑模型

（1）拟合：分别考虑对以天为周期和年（8766h）为周期，按HoltWinters指数平滑法建立时间序列模型。

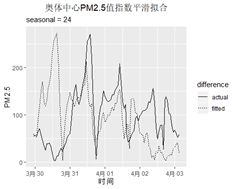
以天为周期的指数平滑建模拟合效果如下，可以看出，拟合效果较好。

以年为周期的指数平滑模型拟合出了大量的绝对值较大的负值，这是不合理的，因此舍弃按年（8766h）为周期的指数平滑模型。

1. 预测：

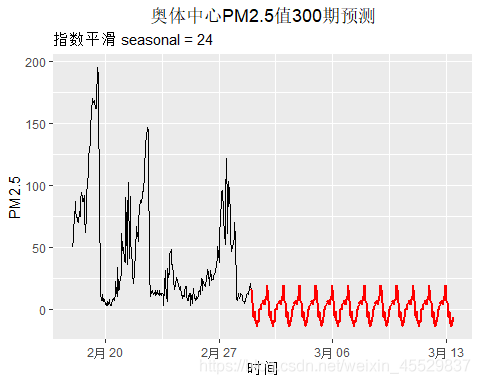
对以天为周期的指数平滑模型进行300阶预测，并绘图如下

可以看出，该模型预测结果存在负值，而且有着明显的完全相同的波动趋势，预测效果十分差。

   2.  模型改进：TBATS模型

①模型介绍：TS 模型全称为Exponential smoothing state space model with Box-Cox transformation, ARMA errors, Trend and Seasonal components，使用了时间序列频域分析法，可以进行多季节性时间序列的建模。由于PM2.5序列既具有一天（24h）的周期，又具有一年（8766h）的周期，所以可以尝试该方法。

②拟合： 先将PM2.5转化为msts格式，再使用tbats()函数。

参数估计结果如下：

  Lambda = 0.347269

  Alpha = 1.073336

  Beta = -0.04546997

  Damping Parameter: = 0.957411

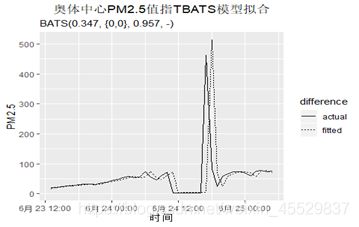
绘制一段拟合图像如下，可以看出拟合效果的十分好，直观上存在过拟合的可能。

③残差检验：原假设为残差是白噪声。在显著性水平为0.05的情况下，拒绝原假设，认为残差不是白噪声。

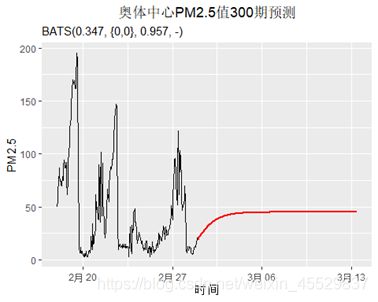
④预测：同样绘制300阶预测图像如下，可以看出其预测效果和ARIMA模型较为相似，即在一定阶数后就只能预测均值而不能预测趋势变化。

 

（四）结果分析

1.模型总体评价

（1）拟合效果：

ARIMA(1,0,2)(0,0,2)[24]和BATS(0.347, {0,0}, 0.957, -)拟合的BIC值分别为314897.3和556018.8，从BIC值越小越好的角度来看，ARIMA模型比指数平滑模型拟合的更好，同时TBATS模型也有过拟合的倾向。

（2）预测效果：

两种模型只能预测一小部分的PM2.5值，近期的观测值对当前值的影响较大，时间越是久远对当前值的影响就越小；当预测阶数继续增大时，预测结果回归到平均水平， 这与模型阶数较低有关，序列的记忆性较短。

根据所绘制的图像，ARIMA(1,0,2)(0,0,2)[24]和BATS(0.347, {0,0}, 0.957, -)效果相似，即只考虑24小时的季节性变化与同时考虑24小时和一年四季的时间序列预测效果相似，推测这是由于以年为周期时，样本量只有4年，建立模型时样本量太少，故无法很好地预测。

2. 模型结论

（1）北京市奥体中心PM2.5时间分布特点

PM2.5基本在0-100的范围内波动，且平均值在50以下，但是一年之中总有一段时间PM2.5的值会处于230-400的范围，甚至是爆表。这说明，北京市奥体中心附近的大气污染一年中的大部分时间相对较正常，小部分时间内大气污染非常严重。

（2）北京市奥体中心PM2.5季节性变化趋势

① PM2.5的变化受季节的影响呈现周期性，总是先上升再减少轮回波动。在一年中，从冬季到夏季呈下降趋势，从夏季到冬季呈上升趋势；这与冬季北京供暖，煤炭焚烧量增大、排放增大的先验信息相符。

② PM2.5在一天中也具有季节性变化，下午的PM2.5值较低，在午夜23时-2时PM2.5值较高，早晚的PM2.5值介于两者之间，这与2013-2017年北京日间不允许大型货车通行、只有午夜允许，且国内存在大量大型货车污染物排放超过国家标准的先验信息相符。

（3）北京市奥体中心未来150小时PM2.5变化

从2017年2月28日23:00起，未来的150个小时PM2.5呈上升趋势，且持续增加的可能性较大。未来的150个小时以后，难以预测出具体的趋势，PM2.5变化的均值仍是45，但其波动难以刻画。

 

 

 

附录一 回归部分代码

一、载入数据

set.seed(1)

path <- "C:/Users/91333/Documents/semiester5/R course/course_assignment/PRSA_Data_20130301-20170228"

fileNames <- dir(path)

filePath <- sapply(fileNames, function(x){

  paste(path,x,sep='/')})  

bj_data <- lapply(filePath, function(x){

  read.csv(x, header=T)})

alldata <- rbind(bj_data[[1]],bj_data[[2]],bj_data[[3]],bj_data[[4]],bj_data[[5]],bj_data[[6]],bj_data[[7]],bj_data[[8]],bj_data[[9]],bj_data[[10]],bj_data[[11]],bj_data[[12]])

Aotizhongxin <- bj_data[[1]]

 

二、绘图

1. 绘制12观测点PM2.5分布盒图

ggplot(alldata,aes(x = reorder(as.factor(station), PM2.5, FUN = mean), y = PM2.5))+geom_boxplot(fill="lightblue",alpha=0.4) +geom_violin(fill="pink",alpha=0.3) +  xlab("station")

 

2. 绘各解释变量与PM2.5的散点图、PM2.5以风向分类的密度曲线

ggplot(Aotizhongxin2, aes(x=SO2,y=PM2.5))+geom_point(alpha=0.1)+geom_smooth()

ggplot(Aotizhongxin2, aes(x=NO2,y=PM2.5))+geom_point(alpha=0.1)+geom_smooth()

ggplot(Aotizhongxin2, aes(x=CO,y=PM2.5))+geom_point(alpha=0.1)+geom_smooth()

ggplot(Aotizhongxin2, aes(x=O3,y=PM2.5))+geom_point(alpha=0.1)+geom_smooth()

ggplot(Aotizhongxin2, aes(x=TEMP,y=PM2.5))+geom_point(alpha=0.1)+geom_smooth()

ggplot(Aotizhongxin2, aes(x=TEMP,y=PM2.5))+geom_point(alpha=0.1)+geom_smooth()

ggplot(Aotizhongxin2, aes(x=PRES,y=PM2.5))+geom_point(alpha=0.1)+geom_smooth()

ggplot(Aotizhongxin2, aes(x=DEWP,y=PM2.5))+geom_point(alpha=0.1)+geom_smooth()

ggplot(Aotizhongxin2, aes(x=RAIN,y=PM2.5))+geom_point(alpha=0.1)+geom_smooth()

ggplot(Aotizhongxin2, aes(x=WSPM,y=PM2.5))+geom_point(alpha=0.1)+geom_smooth()

ggplot(Aotizhongxin2,aes(x=PM2.5,fill=reorder(wd,PM2.5,FUN = median)))+geom_density(alpha=0.3)

 

三、缺失值处理

1．缺失值统计

list("数据集"="Aotizhongxin","缺失值"=sum(is.na(Aotizhongxin_data)),"缺失行"=sum(!complete.cases(Aotizhongxin_data)))

pMiss<-function(x){

  sum(is.na(x))/length(x)*100

}

sapply(Guanyuan_data,pMiss)

含有缺失值的样本大概占总样本的10%左右，但为保证充分利用数据，不首先考虑删除缺失值，CO与O3缺失值比率占其总数据最高，约为5%，缺失较少

 

2. 直接删除

Aotizhongxin<-na.exclude(Aotizhongxin_data)

 

四、 平稳性检验

library(tseries)#ADF检验

list(adf.test(Aotizhongxin$PM2.5),

     adf.test(Aotizhongxin$PM10),

     adf.test(Aotizhongxin$SO2),

     adf.test(Aotizhongxin$NO2),

     adf.test(Aotizhongxin$CO),

     adf.test(Aotizhongxin$O3),

     adf.test(Aotizhongxin$TEMP),

     adf.test(Aotizhongxin$PRES),

     adf.test(Aotizhongxin$DEWP),

     adf.test(Aotizhongxin$RAIN),

     adf.test(Aotizhongxin$wd))

 

五、 多元线性回归

1．建立哑变量

dummy<-model.matrix(~wd, Aotizhongxin)

Aotizhongxin<-cbind(Aotizhongxin[-16],dummy[,-1])

 

2．全变量线性回归

allmodel1 <- lm(PM2.5~., data = Aotizhongxin[,-c(1:5,7,17)])

 

看全变量线性回归拟合效果

plot(allmodel1)

library(car)

vif(allmodel1)

 

 

1.   10折交叉验证筛选变量

library(class)

library(caret)

 

1. 以利用createFolds使得数据集拆分时，PM2.5在十份中分布大体均匀

folds=createFolds(Aotizhongxin$PM2.5,k=10)

str(folds)

 

1. 编写可以利用输入变量建立线性回归、输出MSE的函数

cv_results <- function(yxs){temp1 <- sapply(folds, function(x){

  train = yxs[-x, ]

  test = yxs[x, ]

  actual <- test$regress_y

  test$regress_y <- NULL

  model1 <- lm(train$regress_y~.,data = train)

  pred <- predict(model1, new = test)

  return(sum((actual - pred)^2))

  return(temp1)

})}

regress_x <- Aotizhongxin[,-c(1:7,17)]

regress_y <- Aotizhongxin[,6]

 

1. 以交叉验证为准则，使用backward，进行变量选择

criterion <-  mean(cv_results(cbind(regress_x, regress_y)))

while (TRUE){

temp3 <- colMeans(sapply(1:length(regress_x),function(n){

  cv_results(cbind(regress_y, regress_x[,-n]))

  }

  ))

  if (criterion <= min(temp3)){break}

  regress_x <- regress_x[, -which.min(temp3)]

  criterion <- min(temp3)

}

 

finalmodel <- lm(regress_y ~., data = cbind(regress_x,regress_y))

summary(finalmodel)

 

1. 逐步回归筛选变量

stepmodel <- stepAIC(object=allmodle1, direction = “backward”)

summary(stepmodle)

 

5．模型检验

a. 正态性检验

library(car)

par(mfrow=c(1,1))

qqPlot(stepmodle,main="Q-Q Plot")

b 独立性检验

durbinWatsonTest(stepmodle)#拒绝原假设rho==0，认为随机扰动项存在自相关

c. 线性检验

crPlots(stepmodle)#RAIN不是线性的

d. 同方差检验

ncvTest(stepmodle)

spreadLevelPlot(stepmodle)

e. 模型假设综合检验

library(gvlma)

gvmodel<-gvlma(stepmodle)

summary(gvmodel)

f. 多重共线性

vif(stepmodle)

g. 鉴别离群点

outlierTest(stepmodle)

h. 鉴别强影响点

influencePlot(stepmodle)

 

6．模型改进

a. 对变量取对数

对全部大于0的变量直接取对数，对大于等于0的变量，把0替换为0.01再取对数，对存在负值的变量和哑变量不取对数

logAotizhongxin <- Aotizhongxin

logAotizhongxin$WSPM[logAotizhongxin$WSPM==0] <- 0.01

logAotizhongxin<-cbind(log(logAotizhongxin[,-c(1:5,7,12,14,15,17:32)],logAotizhongxin[,c(12, 14, 15, 18:32)])

allmodel2 <- lm(PM2.5~., data = logAotizhongxin)

library("MASS")

AICmodel2 <- stepAIC(allmodel2, direction = "backward")

plot(AICmodel2)

library(carData)

library(car)

ncvTest(AICmodel2)

durbinWatsonTest(AICmodel2)

 

b. NeweyWest方法修正标准误差

library("AER")

coeftest(stepmodle, vcov. = NeweyWest)

 

 

 

 

 

 

附录二 时间序列部分代码

 

一、初步探索与数据准备

（一）、缺失值补齐

由于需要完整观测，使用KNN方法对缺失值补齐。

require(DMwR)

Aotizhongxin1 <- knnImputation(Aotizhongxin)

（二）、绘图与平稳性检验

由全数据的时间序列图可以看出PM2.5具有以年为单位的时间序列趋势，分月份、星期几、几号、几时画出盒图。

library(ggplot2)
time <- seq.POSIXt(from = as.POSIXct("2013-03-01"), to = as.POSIXct("2017-05-28 23:00:00 "), by = 'hour')
ggplot(Aotizhongxin1)+geom_line(aes(y=PM2.5, x=time[1:35064])) + xlab("时间")+labs(title = "2013-2017年PM2.5折线图")+theme(plot.title = element_text(hjust = 0.5))

由图，我们大致可以看出序列平稳，并且在多元回归部分已经做过ADF检验，数据通过。

（三）、生成ts格式数据

library(forecast)

PM2.51 <- ts(Aotizhongxin1$PM2.5)
PM2.52 <- ts(Aotizhongxin1$PM2.5, frequency = 24)
PM2.53 <- ts(Aotizhongxin1$PM2.5, frequency = 8766)

二、拟合ARIMA模型

(一)、定阶

1. 自相关图和偏相关图法定阶

par(mfrow=c(2,1), mar = c(2,3,5,0), mgp=c(1,0.3,0))
acf(PM2.51, main = "ACF plot of PM2.5_ts")
pacf(PM2.51, main = "PACF plot of PM2.5_ts")

 

1. 根据BIC准则定阶

a. armasubsets函数

根据帮助文档，armasubsets函数使用了长自回归法，使用足够高阶的AR模型来逼近任意平稳序列，先估计逆转形式的参数，近似的求出原模型参数的估计值。

library(TSA)

res <- armasubsets(y=PM2.51, nar=18,nma=25,y.name='test',ar.method='ols')
plot(res)

test-lag1,test-lag2,test-lag12,test-lag13和 error-lag12,error-lag13,error-lag15,error-lag23, 方块最黑，BIC 值最小为93000，那么该函数识别出的模型就是带均值项的 ARMA(13, 23) .

b. auto.arima函数

auto.arima 函数默认使用 AICc 作为最优模型的判断标准，模型默认 allowdrift = TRUE，即考虑均值项。

library(forecast)
fitarima1 <- auto.arima(PM2.51,seasonal = T)
fitarima2 <- auto.arima(PM2.52, seasonal = T)

使用auto.arima的定阶结果为ARMA(1,2)，带有均值项。 由于使用auto.arima得出的BIC小于使用长自回归法得出的BIC，所以arima模型的拟合结果为ARMA(1,2)

（二）拟合与预测

1. 拟合结果

选择最小二乘的方法,arima模型表达式为xt=82.5881+0.9522xt-1+0.1489ϵt-0.0140ϵt-1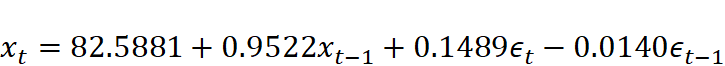

1. 白噪声检验

白噪声检验

Box.test(fitarima1$residuals,lag=2,type='Ljung')
## X-squared = 0.0040207, df = 2, p-value = 0.998

Box.test(fitarima2$residuals,lag=48,type='Ljung')
## X-squared = 286.44, df = 48, p-value < 2.2e-16

对于第一个模型，p>0.05,认为是白噪声 对于第二个模型，p>0.05,认为不是白噪声

1. 预测绘图

forecast_arima1 <- forecast(fitarima1, h = 300)

ggplot() + geom_line(aes(y=c(Aotizhongxin1$PM2.5[34800:35064],forecast_arima1$mean),x=time[34800:35364]))+ geom_point(aes(y=forecast_arima1$mean,x=time[35065:35364]),col="red")+labs(title  = "奥体中心PM2.5值300期预测",subtitle="ARIMA(1,0,2)") +xlab(label = "时间") + ylab(label = "PM2.5")+theme(plot.title  = element_text(hjust = 0.5))

 

forecast_arima2 <- forecast(fitarima2, h = 300)

ggplot() + geom_line(aes(y=c(Aotizhongxin1$PM2.5[34800:35064],forecast_arima2$mean),x=time[34800:35364]))+ geom_point(aes(y=forecast_arima2$mean,x=time[35065:35364]),col="red")+labs(title  = "奥体中心PM2.5值300期预测",subtitle="ARIMA(1,0,2)(0,0,2)[24]") +xlab(label = "时间") + ylab(label = "PM2.5")+theme(plot.title  = element_text(hjust = 0.5))

三、指数平滑拟合

分别考虑以24小时和8766小时为周期的指数平滑

fithot24<-HoltWinters(PM2.52, beta = F)
par(mfrow=c(1,1))
plot(fithot24) 

fithot8766<-HoltWinters(PM2.53, beta = F)
par(mfrow=c(1,1))
plot(fithot8766) 

上面这个以8766为周期的指数平滑拟合就不合理了，出现了比较大的负数值。

（一）、拟合效果

fithot24_plot <- data.frame(PM2.5=c(PM2.51[9456:9556],fithot24$fitted[9456:9556]),difference=rep(c("actual","fitted"),c(101,101)),time=c(time[9456:9556],time[9456:9556]))

ggplot(fithot24_plot)+geom_line(aes(y=PM2.5,x=time,group=difference,linetype=difference))+labs(title  = "奥体中心PM2.5值指数平滑拟合",subtitle="seasonal = 24") +xlab(label = "时间") + ylab(label = "PM2.5")+theme(plot.title  = element_text(hjust = 0.5))

 

（二）、预测效果

forecast_fithot24<-forecast(fithot24,h=300)

ggplot() + geom_line(aes(y=c(PM2.51[34800:35064],forecast_fithot24$mean),x=time[34800:35364]))+ geom_line(aes(y=forecast_fithot24$mean,x=time[35065:35364]),col="red",size=1)+labs(title  = "奥体中心PM2.5值300期预测",subtitle="指数平滑 seasonal = 24") +xlab(label = "时间") + ylab(label = "PM2.5")+theme(plot.title  = element_text(hjust = 0.5))

可以看出拟合结果还凑合，预测结果较差。

(三)、指数平滑法改进

回忆上面的盒图，原数据时间变化，PM2.5的变化是有两方面的，12个月里，PM2.5具有季节性变化，24小时内,PM2.5也有“季节性变化”，考虑多季节性时间序列的建模。

1. 将数据转为msts格式

library(forecast)
PM2.54 <- msts(Aotizhongxin1$PM2.5,seasonal.periods = c(24,8766))

与ts类型相对应，也存在msts的数据类型，并在转化时注明两种季节性变化。

2.tbats拟合

TBATS model (Exponential smoothing state space model with Box-Cox transformation, ARMA errors, Trend and Seasonal components)

De Livera、Hyndman和Snyder（2011）开发的另一种方法使用傅立叶项与指数平滑状态空间模型和Box-Cox变换的组合，完全自动化。

fittbats <- tbats(PM2.54)
fittbats

## BATS(0.347, {0,0}, 0.957, -)
##
## Call: tbats(y = PM2.54)
##
## Parameters
##   Lambda: 0.347269
##   Alpha: 1.073336
##   Beta: -0.04546997
##   Damping Parameter: 0.957411
##
## Seed States:
##             [,1]
## [1,]  0.35764556
## [2,] -0.08296283
## attr(,"lambda")
## [1] 0.3472691
##
## Sigma: 1.154974
## AIC: 556018.8

1. 残差白噪声检验

这里lag的阶数是这个函数的作者建议的2倍周期

Box.test(fittbats$errors,lag=48,type='Ljung')
## X-squared = 221.39, df = 48, p-value < 2.2e-16

Box.test(fittbats$errors,lag=17532,type='Ljung')
## X-squared = 28721, df = 17532, p-value < 2.2e-16

都通不过，认为不是白噪声。

1. 拟合效果

fittbats_plot <- data.frame(PM2.5=c(PM2.51[11510:11550],fittbats$fitted.values[11510:11550]),difference=rep(c("actual","fitted"),c(41,41)),time=c(time[11510:11550],time[11510:11550]))

ggplot(fittbats_plot)+geom_line(aes(y=PM2.5,x=time,group=difference,linetype=difference))+labs(title  = "奥体中心PM2.5值指TBATS模型拟合",subtitle="BATS(0.347, {0,0}, 0.957, -)") +xlab(label = "时间") + ylab(label = "PM2.5")+theme(plot.title  = element_text(hjust = 0.5))

1. 预测效果

forecast_tbats<-forecast(fittbats,h=300)

ggplot() + geom_line(aes(y=c(PM2.51[34800:35064],forecast_tbats$mean),x=time[34800:35364]))+ geom_line(aes(y=forecast_tbats$mean,x=time[35065:35364]),col="red",size=1)+labs(title  = "奥体中心PM2.5值300期预测",subtitle="BATS(0.347, {0,0}, 0.957, -)") +xlab(label = "时间") + ylab(label = "PM2.5")+theme(plot.title  = element_text(hjust = 0.5))